この記事では、ボンフェローニ法(Bonferroni法)による統計学的検定の多重比較でどのような計算をしたらいいのか、そしてメリットやデメリットをお伝えします。
統計学的検定では、様々な場面で多重性の問題が発生します。
臨床試験の場合にも例に漏れず、多重性の問題は統計担当者が一番頭を悩ませる問題。
多重比較をすると問題なのが、全体的なαエラーが増大するということ。
このページでは、その対処法の中で3つ目の「有意水準を補正する」方法を紹介します。
最も有名なのがボンフェローニ法(Bonferroni法)と呼ばれる補正方法です。
ボンフェローニ法とは?統計検定で多重比較の際に有意水準を補正する方法

検定の多重性を回避する方法として、有意水準を補正する方法がありました。
どんな場面で有意水準を補正するか。
検定を一つにも絞れず、かつ検定の優先順位(順番)もつけることができない場合
そんな場面であれば、有意水準を調整する方法にします。
つまり、最終手段の方法ですね。

ではなぜ、検定を1つに絞ったり、優先順位をつけたりする方法を優先して使ったほうがいいのか。
その理由は、明確なメリットがあるからです。
検定を1つに絞ったり、優先順位をつけたりする方法のメリット。
有意水準を5%にしたまま検定できる
だから、最初は検定を1つに絞ったり、優先順位をつけたりする方法を検討したほうがいいのです。
では、どうしようもなく検定を複数回実施しなければならない場合。
有意水準を補正します。
そして有意水準を調整する方法がいくつか開発されています。
具体的にはボンフェローニ(Bonferroni)法、ホルム(Holm)法、そして多重比較検定であるダネット(Dunnett)検定やテューキー(Tukey)検定などです。
今回の記事では、直感的かつ数学的にもイメージしやすいボンフェローニ法を紹介します。
ボンフェローニ法で有意水準を補正する場合、どんな計算式なのか

ボンフェローニ法の有意水準の補正方法は簡単です。
通常の有意水準をα(普通は0.05)、実施する検定の数をNとする場合に、一つ一つの検定の有意水準をα/Nにするという方法です。
例えば、有意水準が0.05で、検定を2回実施したい時。
それぞれの検定の有意水準を0.05/2=0.025に調整するのです。
そして検定の結果、P値が0.025を下回れば、有意になります。
決して、0.05を下回ったからといって、有意にはならないので注意してください!
重要なのでもう一度書きます。
検定を2回実施した場合、Bonferroni法で有意水準を調整して検定したら、P値が0.025を下回って初めて有意になる
では、検定が5つの場合は。
一つ一つの検定の有意水準を0.05/5=0.01にして、P値が0.01を下回る場合に有意という結論を得ます。
つまり、このようになりますね。
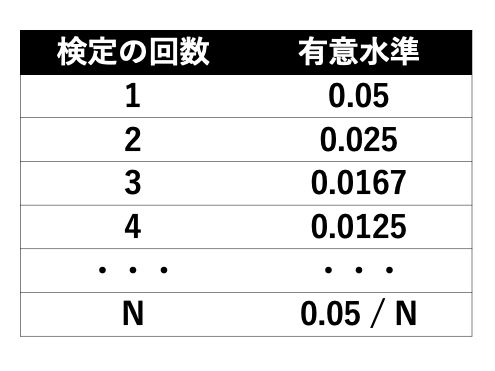
この方法はとても直観的であり、かつ簡単に実施しやすい方法ではあります。
ですが、他の有意水準の調整方法よりも一番厳しい、つまり一番有意になりにくい方法であるといえます。
ボンフェローニ法などを使って有意水準を補正するとなぜαエラーが増大しないのか?
ボンフェローニ法で有意水準を補正する計算式はわかりました。
αエラーを検定の回数で割るだけなので、特に難しくありませんでしたね。
では、なぜそのような有意水準の補正をするだけで、αエラーの増大が防げるのか?ということです。
以下の図のように、1回だけ検定をした場合、αエラーは全体(100%)の中で5%を占めます。

では、2回検定をした場合にはどうなるでしょうか。
その場合にαエラーは以下のようになります。

1回目のαエラーと2回目のαエラーがあり、その一部が重なっているような図です。
このとき、2回検定をして1回でもαエラーが生じる確率は、2つの円の総面積になります。
つまり、このときのαエラー「0.05+0.05-0.05*0.05=0.0975」となってしまうのです。
0.0975は有意水準で設定した0.05より大きいため、問題となります。
しかし、ボンフェローニ法で有意水準を補正してあげると、1つ1つのアルファエラーが0.025になるため、以下のような図になります。
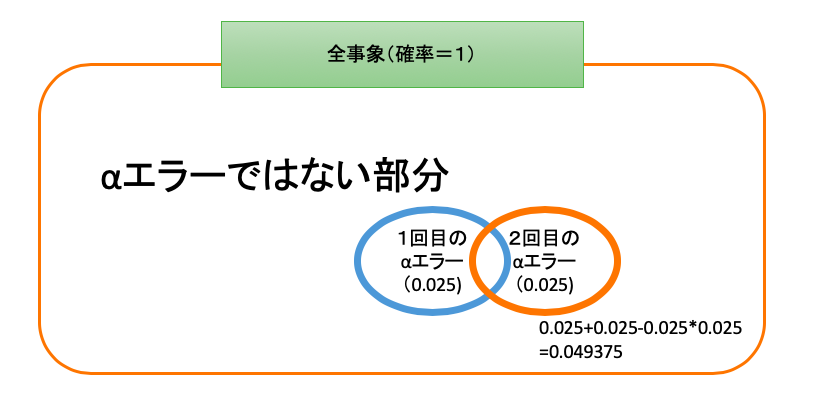
そのため、2回検定をして1回でもαエラーが生じる確率は、2つの円の総面積の0.049375となります。
そうすると、有意水準である0.05よりも小さいαエラーで2回の検定をすることができることになります。
ボンフェローニ法で有意水準を補正するデメリット

計算が簡単で、直感的に理解しやすいボンフェローニ法。
しかし、この方法には問題点があります。
それは検出力が低くなってしまうこと。
検出力が低いということは、本来であれば有意差が出るはずのデータなのに有意差が付きにくい、ということです。
統計的な用語を使うと「保守的な」検定方法です。
なぜならば、本当は有意水準を0.05として設定していいですが、前述の通り2回検定した場合に0.049375のαエラーになります。
0.05-0.04375=0.00625だけ、有意差が付きにくくなっている、ということ。
ほんのちょっとの違いのように思いますが、この数字の差はかなり大きいのです。
この保守的な側面を解決するために、ホルム(Holm)法や多重比較検定であるダネット(Dunnett)検定やテューキー(Tukey)検定などが開発されました。
ボンフェローニ法に関するまとめ

多重性の対処法の中で、有意水準を調整する方法は、最後に選択する最終手段。
Bonferroni法は直感的で、簡単に実施しやすい調整方法。
しかし、他の調整法と比べて有意になりにくい、保守的な方法とも言える。
Bonferroni法は分散分析の後の事後検定としても使われることがあります。
動画でも多重性の問題とボンフェローニ法の解説をしていますので、記事内容と合わせてご確認いただけると理解が進むかと思います。










コメント
コメント一覧 (5件)
[…] […]
大変分かりやすい解説ありがとうごさいます。質問させて頂きます。ボンフェローに関して検定の結果のP値を検定の回数で割るという説明ですが、他の説明ではP値に検定の回数を掛けるとあります。P値の補正をおこなう場合に検定の回数で割る、掛けるどちらが正しいのでしょうか? 大変お忙しいとは思いますがなにとぞ、ご教示頂きたくお願い申し上げます。
本質的にはどちらも同じなので、どちらも正しいかと思います。
今まで見てきた教科書的には、有意水準を割る方がメジャーではないかと思いmさう。
[…] 多重比較の詳細はこちらの記事をご覧ください。 […]
[…] ボンフェローニ法での補正は多重比較検定で重要!計算方法や … […]