この記事では「年齢など患者背景の有意差はどんな意味があるのか?論文にP値で示すことの問題点」としてお伝えします。
患者背景の比較では必ず統計学的検定を実施する、というのが慣例になっている印象があります。
しかしながら、近年では患者背景の比較に対してP値で何かを示すことは減少傾向にあるんです。
そのためこの記事では
- 患者背景の検定(P値)で何が示せるのか?
- 患者背景を比較するそもそもの目的は?
- トップジャーナルでは患者背景の比較をどのようにしているのか?
といったことをお伝えしていきます!
患者背景の検定結果(P値)に対して研究者が期待していること

まずは、そもそも患者背景に対して検定することによって、研究者自身は何を期待しているのか?ということを整理してみましょう。
ここでは、2群間の比較試験を想定します。
2群比較の場合、通常は患者背景の要約では群ごとに要約統計量を記載します。
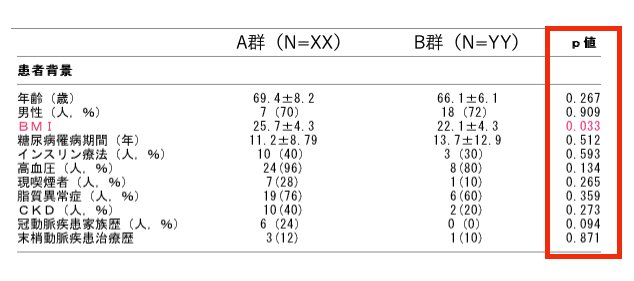
その際に、上記のように統計学的検定を用いて群間比較をしているのをよく見ます。
例えば、年齢、体重などの連続変数(量的データ)の場合には、T検定(正規分布の場合)やマンホイットニーのU検定(正規分布じゃない場合)が使われます。
性別、人種などのカテゴリカル変数(質的データ)であれば、カイ二乗検定やフィッシャーの正確確率検定が使われているのをよく見ます。
統計学的検定をおさらいする
ここでちょっと、統計学的検定をおさらいしましょう。
統計学的検定を実施すると、「有意差あり」か「有意差なし」の2択の結論が出ます。
有意差がある場合、帰無仮説を棄却することになり対立仮説を採択することになります。
例えばT検定の対立仮説は「2群間の平均値に差がある」ですので、有意差がある場合には「群間に差がある」を採択することができます。
では有意差がなかった場合。
この場合は「帰無仮説を棄却できない」ということになります。
T検定であれば帰無仮説は「群間の平均値に差がない」ですから、「群間の平均値に差がない」を否定できないということ。
言い換えると、今回のデータでは群間に差があるとはいえない、ということなんです。
私が何を言いたいかと言えば、統計学的検定で有意差がなかった場合に、群間で「同じである」はいえない、ということ。
ここは重要なポイントです。
統計学的検定をおさらいすると、患者背景の群間比較では問題解決になっていないことがわかる
患者背景で群間比較をすることは、研究者としては「群間で差がない」ことを期待しているわけです。
なぜかと言えば、群間で差があると
ということになるので、できれば群間で同じである方が解析をシンプルにできるから。
ですが、有意差がないことを確認しても「今回のデータでは群間に差があるとはいえない」しか示すことができないため、「群間で同じである」ということは積極的にいえないんです。
つまり、
- 「群間で差がない」ことを示したいけど、統計学的検定では仕組み上、それを示すことができない
- しかも有意差があっても、それは単に症例数が多かっただけの可能性もある
ということを考えると、患者背景を統計学的検定で示したとしても、根本解決にはなっていない可能性が高い、ということなんです。
患者背景を比較してP値を提示する意味

再度「患者背景を比較する意味」を考えたいのですが、患者背景を比較する理由は「交絡バイアスを引き起こす可能性のある因子がないかどうかを確認したい」ということ。
では、交絡バイアスはどんな時に引き起こされるかと言えば、アウトカムに影響を与える因子が群間で偏っている場合に生じます。
つまり、交絡バイアスが引き起こされる条件は2つ。
- アウトカムに影響を与える因子である
- その因子が群間で偏っている
例えば、アウトカムが体重だった時。
- 性別は体重に影響を与える(女性は軽く男性は重い傾向にある)
- もし仮に群間で男女比が偏っていたら、体重(アウトカム)の違いは「群の違い」なのか「男女比の違い」なのかがわからなくなる
ということが言えます。
そして仮に患者背景の検定を実施するとしても、交絡バイアスの条件の2番目(因子が軍艦で偏っている)しか確認していることにならないわけです。
つまり、条件の1番目の視点(アウトカムに影響を与える因子である)は抜け落ちてしまっています。
しかも、条件の1番目は患者背景を比較しなくても確認することができますし、むしろ比較ではわからない部分になります。
論文において、患者背景で有意差を示すことで言えることは少ない

今まで見てきたことを整理すると
- 被験者背景では「群間で差がない」ことを示したいけど、統計学的検定では仕組み上、それを示すことができない
- しかも有意差があっても、それは単に症例数が多かっただけの可能性もある
- 交絡バイアスの条件の1番目の視点(アウトカムに影響を与える因子である)は抜け落ちてしまっている
ということが言えます。
であれば、患者背景で有意差があるかどうかという情報の価値って、実はそれほど大きなものではなかったりします。
じゃあ重要な点はどこなのか?と言えば、まずは交絡バイアスの条件の1番目の視点(アウトカムに影響を与える因子である)を考えることかなと思います。
そしてその因子は、患者背景の群間比較で有意差があろうがなかろうが、交絡バイアスの調整(ex. 多変量解析の説明変数)に入れるということを事前に決めておくことが重要。
では、患者背景の検定結果は全くもって不要なのか?と言われれば、そうでもないなとも個人的には思います。
なぜなら、群間でどれぐらいの違いがあるのかをざっと確認するには、P値は便利な指標だと思うからです。
しかし、P値は症例数に依存する指標なので、結局は平均値の差や割合の差を確認することの方が大事ということは間違いありません。
トップジャーナルでは患者背景の有意差に関してどうなっているか?
では最後に、トップジャーナルではどうなっているかを見ていきましょう。
一つの例ですが、こちらの論文は後ろ向き研究だけど群間比較のP値が記載されていません。

(https://www.nejm.org/doi/full/10.1056/NEJMoa2021680)
後ろ向き研究であれば、群間で背景情報が偏っていることはむしろ普通かなと思いますが、それでも統計学的検定を実施してP値を示すことはしていません。
古い論文だと患者背景のP値が出ているものも確かにありますが、最近ではASA(アメリカ統計協会)の声明もあり、P値を出力しない傾向になっていますね。
背景情報を揃えることが目的の傾向スコアマッチングでも、患者背景の比較はP値では記載されません。
では何で比較しているかと言えば、P値ではなく標準化差です。
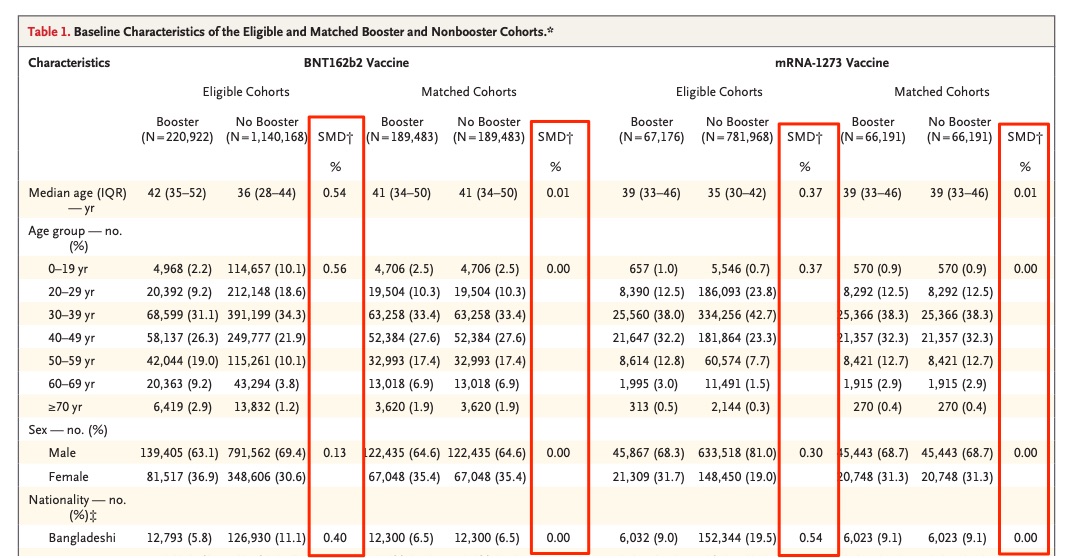
上記のように症例数が非常に多い研究だと、意味のない差に対しても全部の指標に有意差が出てしまいます。
しかし標準化差は症例数に依存しない指標ですので、オールラウンドに使えますね。
まとめ

いかがでしたか?
この記事では「患者背景の有意差はどんな意味があるのか?P値で示すことの問題点」としてお伝えしました。
- 患者背景の検定(P値)で何が示せるのか?
- 患者背景を比較するそもそもの目的は?
- トップジャーナルでは患者背景の比較をどのようにしているのか?
といったことが伝わったのなら幸いです!













コメント