多重性の調整方法は？閉手順など検定の多重性を補正する3つの方法

統計学的検定の多重性は、医薬研究でかなり問題となります。

多重性の問題が、試験の計画段階で統計の専門家が一番頭を悩ませる点といっても過言ではありません。

そんな検定の多重性の問題ですが、調整する方法はあるのでしょうか？

 

この記事では、まずは医薬研究で多重性が発生する状況をまとめます。

そして、統計学的検定の多重性を補正する方法を3つ紹介します！

 

多重性を調整する必要がある状況：検定を2回以上実施すれば多重性の問題は起こる

多重性は、複数回の検定（2回以上の検定）を実施する際に起こる問題です。

なぜ２回以上検定をすると問題なのか。

それは、試験全体としてαエラーが大きくなってしまうからです。

統計的検定が有意水準を５％として設定していることは、誰もが知っていますよね。

そのαエラーが５％を超えてしまうということは、とても重大な問題であると認識できるかと思います。

 

それでは、臨床試験ではどのような状況で多重性の問題が出てくるでしょうか？

具体的には以下の３つの状況が考えられます。

 

 

どういう状況か、もう少し考えてみましょう。

 

多重性の調整が必要な状況1：主要エンドポイントが複数ある場合

これは一番イメージしやすい状況かもしれません。

主要エンドポイントを複数設定し、そのうち「どれか一つでも達成」すれば試験の目的を達成する。

そんな状況であれば、多重性の問題が発生します。

 

例えば、アトピー性皮膚炎という疾患があります。

この疾患は、皮膚炎とかゆみの2つの特徴を持つ疾患です。

その時、主要エンドポイントを「皮膚炎の改善」と「かゆみの改善」の2つにしたとします。

皮膚炎だけが改善すればアトピー性皮膚炎の薬として申請し、かゆみだけが改善すればアトピー性皮膚炎に伴うかゆみの改善薬として申請する。

上記のような戦略を取るのであれば、どっちかのエンドポイントで達成できなくても、申請ができる。

これではいいとこ取りになりますよね。

つまり、多重性の問題があるということになります。

 

多重性の調整が必要な状況2：比較する群が複数ある場合

この状況も、多重性の問題が出てきます。

例えば、Phase II試験までに用量を決めきれずに、実薬群は低用量と高用量の2用量でPhase III試験を実施したとします。

すると、

1. プラセボ群
2. 低用量実薬群
3. 高用量実薬群

の3群で試験を実施することになります。

 

この時Phase IIIの比較は「プラセボ群vs低用量群」「プラセボ群vs高用量群」の2つの比較をすることになります。

その際に、どちらか一方でも有意になればその用量で申請するという戦略にしている場合、この時にも多重性の問題が出てきます。

 

多重性の調整が必要な状況3：解析する時点が複数ある場合

2つ目の状況は、解析する時点が複数ある場合です。

具体的にいうと、中間解析を実施する場合です。

例えば、1年間の試験の場合に、半年時点で一回解析を計画するような場合。

この時に、

1. 試験開始から半年後に1度検定する
2. 試験開始から1年後に2回目の検定をする

というように、2回の検定をすることになりますね。

そして、半年時点もしくは1年時点のいずれかの結果が有意であれば試験の目的を達成するという状況であれば、これも多重性の問題が出て来ます。

また、中間解析ではなくとも、経時的にデータを取得し、いずれかの時点で有意かどうかを判定する際にも、多重性の問題が発生します。

 

複数検定する場合でも、多重性の調整が必要ない状況

複数の検定を実施する場合でも、多重性の問題が出てこない状況があります。

それは「複数の検定全てで有意になる場合に目的を達成する」場合です。

例えば2つの主要エンドポイントがあった時に、どちらか一方が有意になれば試験の目的を達成する場合には多重性の問題が出てきますが、どちらも有意にならない限り試験の目的を達成しない、というような場合には多重性の問題が出てきません。

さいころの例だと、2回投げた時に、どちらか1回でも6が出る確率というのが多重性の問題が発生する状況ですが、2回とも6が出る確率というのは1回よりも厳しくなります。

そのため、αエラーという観点では、「どちらか一方をいいとこ取りする」という状況でなければ多重性の問題が発生しないのです。

AもしくはBの状況では多重性の問題が発生しますが、AかつBの状況では多重性の問題が発生しません。

 

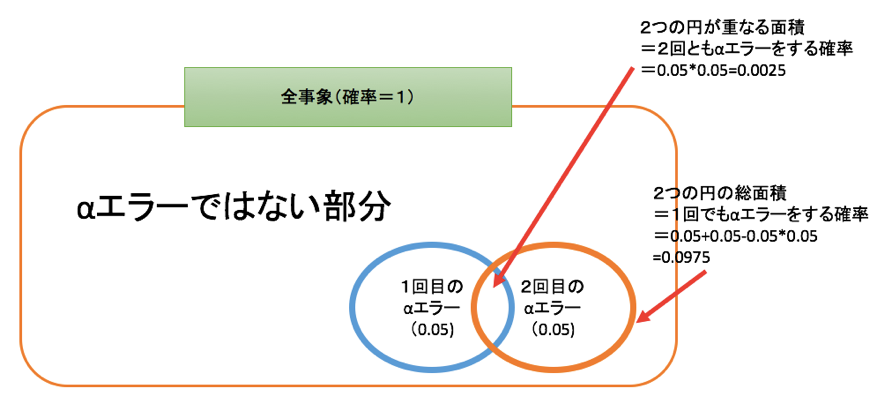
少しだけ、αエラーを図式化してみます。

1回だけ検定をした場合、αエラーは全体（100%）の中で5%を占めますね。

では、２回検定をした場合。

その場合には、以下のような図になります。

１回目のαエラーと２回目のαエラーがあり、その一部が重なっているような図です。

この時、「もしくは」の状況（１回でもαエラーが生じる確率）は二つの円の総面積になります。

つまり、0.05+0.05-0.05*0.05=0.0975となります。この0.0975が0.05より大きいため、問題となります。

ですが、「かつ」の状況（２回ともαエラーが生じる確率）は二つの円が重なっている面積になります。

つまり、0.05*0.05=0.0025となります。この0.0025は0.05よりも大きいので、多重性という点では問題ないことになります。

 

 

閉手順など多重性を回避する３つの方法は？

複数回検定してそのうちどれかが有意になる場合、多重性の問題が生じます。

では、どうすれば多重性の問題を回避することが出来るでしょうか？

よく行われる回避方法としては、3つ挙げられます。

 

 

では、この３つに関して詳細にみていきましょう。

 

検定をどうにか一つにする

これは、多重性を回避するのに一番シンプルな方法です。

複数回の検定に問題があるのであれば、一つにすればよいということです。

主要エンドポイントが複数あれば、一つに選ぶか、複数のエンドポイントを合成して一つにしてしまう（合成変数の作成）がアイデアとして挙げられます。

合成変数を作成する場合には、その変数がちゃんと使えるかどうかという評価をしなければならない、という新たな問題が出てくるため、一つに選ぶという方法が一番シンプルになります。

 

閉手順：検定に順番を付ける

これは、閉手順という用語として知られる手法です。

複数回検定をする場合であっても、そこに順番を付けることで多重性を回避することが出来ます。

具体的には、このような手順です。

 

 

この方法によってなぜ多重性の問題が回避できるのか。

それは、「いずれかが有意である」という状況を避けることができるからです。

多重性の問題とは、複数回検定をする、ということ自体に問題があるわけではありません。

複数回検定をして、どれか一つが有意になればOKという状況にある、ということが問題です。

 

そのため、「いずれかが有意である」という状況を避けることができるこの「検定に順番をつける」というのは多重性の問題の回避につながるのです。

そして、ここも重要なのですが、この検定の順番というのも、事前に決める必要があることに注意しなければなりません。

 

有意水準を調整する

これは最終的な手段になります。

どうしても複数回の検定を実施し、いずれかの結果によって試験の目的を達成することを言いたい場合、有意水準を調整する必要があります。

例えばボンフェローニ法の場合、2回の検定を実施するのであれば、通常は5%にしている有意水準を2.5%にして2回検定を実施します。

その場合には、P値は0.025を下回らなければ有意という結論は出せなくなります。

 

多重性の調整方法まとめ

医薬研究で多重性の問題が発生する状況として3つ例をあげました。

1. 主要エンドポイントが2つ以上ある場合
2. 比較する群が複数ある場合
3. 解析する時点が複数ある場合

よく行われる多重性の回避方法も3つあります。

1. 検定をどうにかして一つにする
2. 検定に順番を付ける
3. 有意水準を調整する