有意水準と有意差とp値とは？5%の意味や決め方・求め方をわかりやすく簡単に

・有意水準、有意差、P値ってどうやって使い分けるの？

・そもそもこの３つ、何が違うの？

・なぜ有意水準って5%なの？

 

私の周りを見渡しても、有意水準、P値、有意差の３つを正確に使い分けられている人は、かなり少ないようです。

今回の記事では、この「有意水準」「有意差」「p値」の意味や決め方を、わかりやすく簡単に解説します。

 

有意水準、有意差、P値とは？わかりやすく言うと？

有意水準、有意差、P値の3つ。

これには実は、順番があります。

順番というか、ピラミッド構造。

私の概念では、こう。

 

 

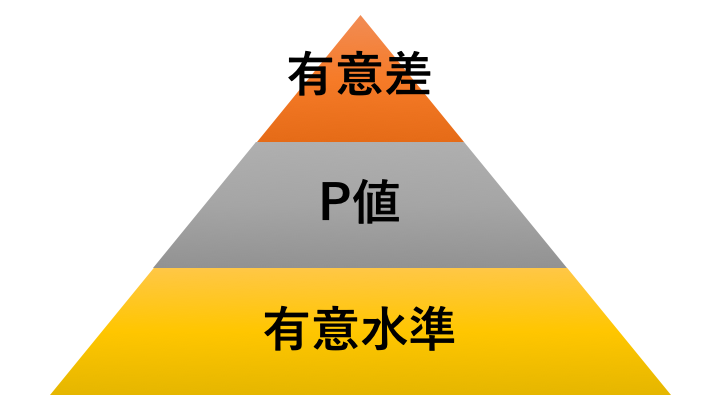
言葉にすると、こんな感じです。

 

 

・・・このままでは全然わからないですよね。。

 

でも大丈夫です。

わかるようになります。

まずは、一つ一つの用語を整理しましょう。

 

有意水準とは？どんな意味？

まずは、ピラミッドの一番下にある有意水準。

「水準」という言葉がついています。

「水準」ということは、何かの「基準」である、ということが想像できますね。

基準とは、Wikipediaによるとこのような説明です。

 

基準（きじゅん）とは、行動や判断の根拠となる物や数値である。何かを比較する時に用いる。

 

例えば赤点では、あなたの試験の点数が40点を下回ると、赤点と判断されます。

つまり、この時の「40点」が「赤点」の判断の基準です。

 

もう一つ、高度肥満の基準。

 

BMIが35を上回ったら、高度肥満と認定です。

そのため、「BIM=35」が「高度肥満」という判断の基準です。

BMIがその基準を上回った時に、高度肥満という意味を持たせる。

 

では話を戻して、有意水準は何の基準か。

そう、「有意」かどうかの判断基準ですね。

つまり有意水準とは、何かが有意水準を下回った時に、「有意差あり」と意味づけする「基準」です。

つまり有意水準は、高度肥満のBMI＝35と同じ意味合いを持ちます。

 

有意水準と比べる対象：P値とは？

有意水準が、ある「基準」ということがわかりました。

では、今度は「何が」有意水準を下回れば良いかという問題です。

これはもう、タイトルの通り。

そう、P値です。

 

 

ちなみに、P値のPってなんの略か分かりますか？

答えは、Probabilityです。

日本語では確率です。

そう、P値って確率のことです。

P値とは、帰無仮説を考えたときに、その結果が出る確率を意味します。

 

有意差とは？有意水準とP値がわかると、わかりやすくなる

今までの知識をまとめると、「有意差」「有意水準」「P値」の3つの用語の関係は以下のようになります。

 

 

結構わかりやすいですよね。

先ほどの赤点のケースと、今回の有意差の話を表にすると、以下のようになります。

 

	赤点の例	有意差
基準	40点	有意水準
比較するもの	試験の点数	p値
判断結果	試験の点数＜40点で、赤点と判断	p値＜有意水準で、有意差ありと判断

 

どうでしょうか？

知識がクリアになりましたか？

 

 

P値を計算する前に有意水準を決めておかなければならない理由

「有意差」「有意水準」「P値」の3つの用語と使い方が分かったところで、もう少し深く理解していきましょう。

 

有意差がある時、実は2パターンでてきませんか？

もう一度、有意差がある時に「有意水準」と「P値」がどのような関係だったか見てみましょう。

 

有意水準＞P値

 

 

有意差ありと判定されるパターン１

１つ目のパターンは、P値が小さい時。

当然この時は、有意差あり、と自信を持って言えますね。

例えば、P値が0.000001という結果になったら、自信を持って「有意差あり」と言えます。

 

有意差ありと判定されるパターン２

二つ目のパターンは、有意水準が大きい時。

この時も、有意差ありって言えませんか？

例えば、P値が0.2だった時。

有意水準を0.3に設定していれば、有意差＞P値の関係が保てます。

そう、有意差あり、と判断できますね。

 

（そんなのズルだろ・・・）

（ただのイチャモンじゃないか・・・）

 

そんな声が聞こえてきそうです。ww

でも、理論上は可能なんです。

一般的に、そして常識的に、有意水準は0.05としています。

ですが、実はそうじゃなくてもいい。

だって、ただの基準だから。

有意水準を動かしてしまえば、どんなP値でも有意差が出てしまう。

 

だから、ピラミッドの一番下なんです！

有意水準をP値の後に動かしちゃうと、有意差が100%出ちゃうんです！

後出しジャンケンと一緒！

 

 

そこで医薬品開発では、有意水準を0.05(5%)にするということが決められています。

正確には、両側の有意水準が0.05です。

 

冒頭で「有意水準があってP値に意味を持たせる」と言った意味がわかりましたでしょうか？

ではここまでを、肥満の例を踏まえて表でまとめてみます。

先ほどの赤点と同じですね。

 

	高度肥満症	有意差
基準	BMI=35	有意水準（0.05）
基準と照らし合わせる指標	BMI	P値
どうなる？	BMI>35で、高度肥満症	P値＜有意水準で、有意差あり

 

P値を計算する前に有意水準を決める必要性：有意差ありとするかは有意水準次第だから

繰り返しになりますが、統計学的検定は手順（順番）がめちゃめちゃ重要です！

有意水準がボーダーラインであることを知ると、有意水準はP値を出力する前に、事前に定める必要があるということが分かります。

つまり、P値を算出してから有意水準を決めたのでは、後出しジャンケンと一緒だからです。

P値が0.08だったから、有意水準は0.1にしてしまえ！

というスタンスでは、全くその検定に意味はなくなってしまいます。

 

そのため、検定にはちゃんと手順があるのです。

という手順です。

2と3を入れ替えてしまうと、極端な話、全ての検定を有意にすることが可能です。

赤点の例でもそうですよね。

採点した後に「やっぱり今回の赤点のボーダーラインは50点にする」と言われたら、クレームが来るのは目に見えています。

 

有意水準はなぜ5%にしなければならないのか？決め方は？

「有意差」「有意水準」「P値」の3つがわかると、次に疑問が出てくるのは「なぜ有意水準は5%なのか？」ということ。

 

10%じゃダメなのか？

1％にしなくてもいいのか？

 

そんな疑問が出てきても良いはずです。

 

結論から言うと、有意水準が5%と決められている明確な基準はありません。

噂では、統計家として大変有名なフィッシャーさんが、決めたものだと言われています。

フィッシャーさんとは、フィッシャーの正確確率検定を発見した人です。

 

フィッシャーさんは、「有意水準を0.05にすると便利だ」という主張をしています。

便利である理由は、平均μ、標準偏差σの正規分布に従う確率変数がμ±2σの範囲外の値を取る確率（つまり、平均から標準偏差の2倍以上外れる確率）がほぼ5%でわかりやすいから、ということです。

 

しかし、科学的な根拠はないため、それぞれの分野によってよく使われる有意水準を使う、というのが正解です。

 

P値とは？コイン投げの例でわかりやすく

P値についても補足しておきます。

P値の定義を再度確認します。

 

P値とは、帰無仮説下でその結果以上（以下）が得られる確率

 

ここで出てきた用語は「帰無仮説」ですね。

帰無仮説とは、本来証明したい仮説ではなく、無に帰したい仮説のことです。

 

 

コイン投げを例にしてP値を理解していきましょう。

数式はほとんど出ていませんので。

 

コインって、表が出る確率は50%ですよね。

じゃあ、100回コインを投げた時。

50回表が出たら、それはまぁ確かに普通のコインだな、と思いますよね。

45回表が出たとしても、それはそれで納得できると思います。

そりゃ、たまたま45回になることもあるよ、と。

 

では、1回しか表が出なかった時。

「・・・ありえないでしょ！！」って思いませんか？

つまり、コイン投げで表が出る確率を50%だと思っていると、表が1回しか出ないというのはあり得ない。

だから、表が50%のコインではない！

イカサマだーー！！

こう思うのが普通です。

 

 

この時、表が出る確率50%を帰無仮説と言います。

その帰無仮説を考えた時に、表が1回以下しか出ない確率をP値とよびます。

ちなみに、100回中1回しか表が出ない時のP値は、もはや天文学的に小さいです。

 

このコインの例を、統計用語を使ってまとめます。

 

 

これが全容です。

わかりましたか？

有意水準、P値、有意差に関するまとめ

有意水準、P値、有意差の3つには順番がある。

この順番を間違えると、いくらでもイカサマができる。

 

有意水準は、有意かどうかを決めるための基準であり、普通は0.05。

P値は、有意水準と照らし合わせるための数字。

有意水準＞P値という結果になった時に、有意差あり、と結論づける。

 

 

また、こちらの記事を、動画で解説しています。

記事と動画を合わせて確認すると、理解がすごく進むと思います。