この記事では「重回帰分析での交互作用項は中心化したほうがいい?多重共線性の解消方法」としてお伝えします。
- 重回帰分析で連続変数を含む交互作用項がある場合に勝手に中心化されることがある
- 中心化(センタリング)って何?
- 中心化することで本当に多重共線性の問題は解決する?
ということを分かりやすく解説していきます!
架空のデータで実際に中心化してみた結果もお伝えしますので、ぜひ見てみてください!
重回帰分析で連続変数を含む交互作用項がある場合に勝手に中心化されることがある
重回帰分析をはじめとする回帰分析において交互作用項を入れたいときが、たまにあるかもしれません。
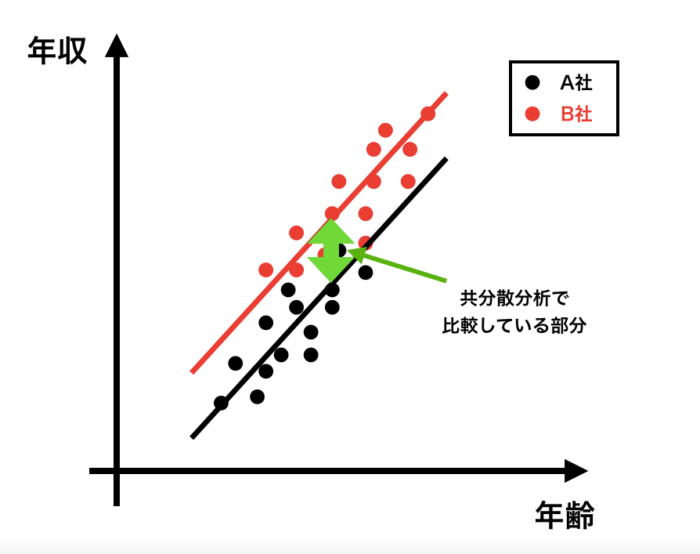
例えば、下記のように群間で共変量とアウトカムの直線関係が平行ではないときですね。
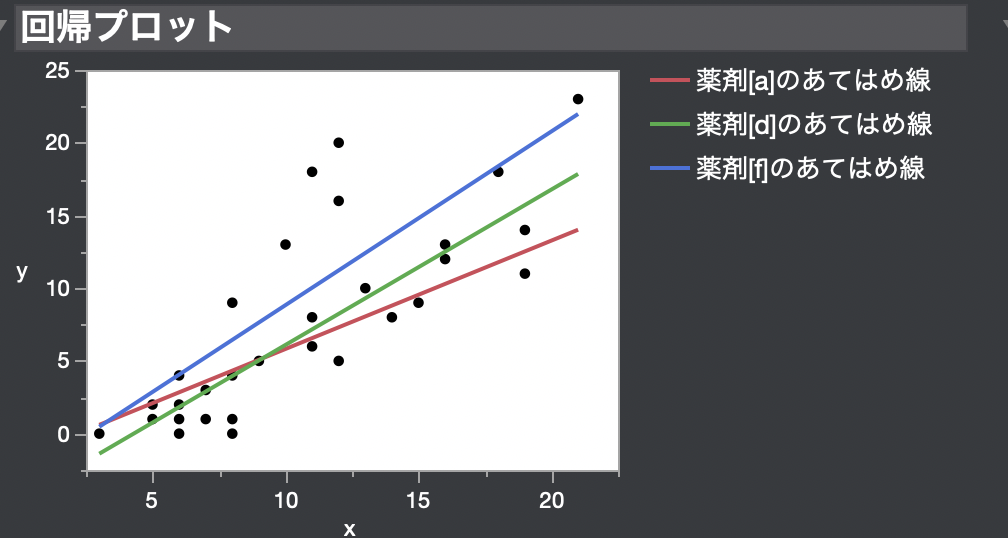
なぜなら、交互作用項を入れない場合は、群間で直線が平行であることを仮定しているからです。
JMPで連続変数を含めた交互作用項をモデルに含めると謎の定数が引き算されている
例えば、JMPを使って連続変数を含めた交互作用項をモデルに含めた場合、解析を実施すると謎の定数が引き算されていることがわかります。
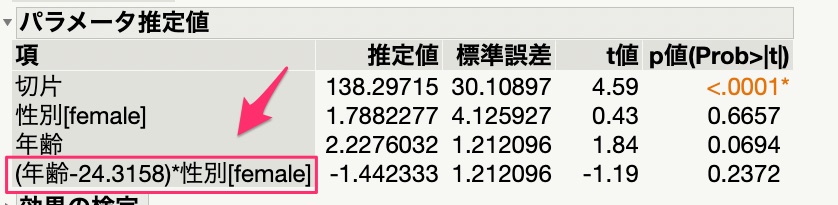
年齢から「-24.3158」という数字が引き算されて解析されています。
これ、何なの。。。ってなりますよね。
結論から言えば、その定数は年齢(交互作用項に入っている連続変数)の平均値です。
連続変数から平均値を引くことを「中心化(センタリング)」と呼び、JMPでは連続変数を含めた交互作用項をモデルに含めた場合、勝手に中心化(センタリング)してくれるんです。
中心化(センタリング)って何?

では、そもそも「中心化(センタリング)」とは何で、どんな意味を持つのでしょうか?
「中心化(センタリング)」を考える上で、回帰モデルに交互作用項を含める場合の問題点を考えてみましょう。
交互作用項が単独で回帰モデルに入っていることはほとんどなく、その変数が単独で入っていることがほとんどです。
回帰モデルに交互作用項を含める場合の問題点として、他の説明変数との相関が高くなる可能性がある、ということが挙げられます。
先程のJMPの例の場合、「年齢」と「年齢*性別」の相関が高くなってしまう、という問題ですね。
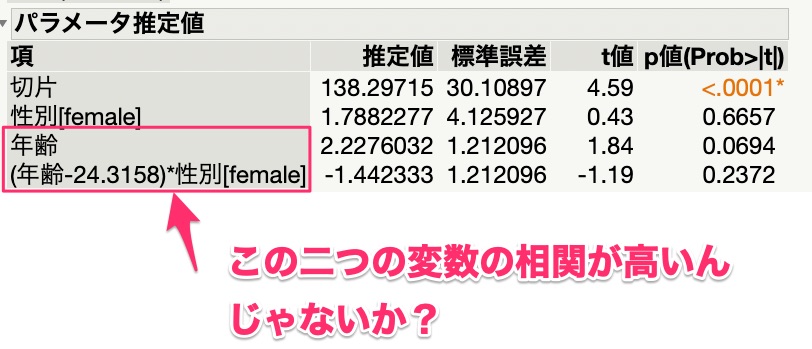
説明変数として含めている変数同士の相関が高いということは、多重共線性の問題が出てきてしまう、という問題に発展します。
多重共線性が発生すると、ちゃんとした解析結果を出してくれないことになるので、かなり大きな問題になります。
そのため、多重共線性の問題を解決するための一つの方法が中心化(センタリング)なのです。
中心化(センタリング)自体はそれほど難しくなく、連続変数に対して平均値を引き算すればいいだけです。
中心化することで本当に多重共線性の問題は解決する?
「中心化(センタリング)」は多重共線性の問題に対する解決策の一つであることが理解できました。
では、本当にそうなのか?を、架空のデータで考えてみましょう。
下記のようなデータがあったとします。
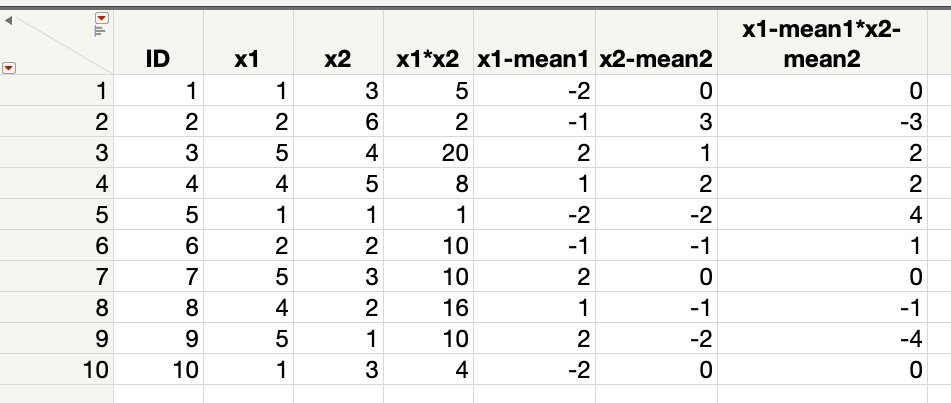
各変数が意味していることは下記の通り。
このときに、
- x1, x2とx1*x2の相関はどうか?
- x1, x2とx1-mean*x2-meanの相関はどうか?
この2つの相関係数を確認してみましょう。
元の連続変数と交互作用項との相関
まずは「x1, x2とx1*x2の相関はどうか?」を確認してみます。
相関係数を計算してみると、下記のような値になりました。

「x1」と「x1*x2」の相関係数が大きいことがわかります。
0.75の相関ってなかなか大きいですから、多重共線性の問題が懸念されますね。。
連続変数と中心化した後の交互作用項との相関
では次に「x1, x2とx1-mean*x2-meanの相関はどうか?」を確認してみます。
相関係数を計算してみると、下記のような値になりました。
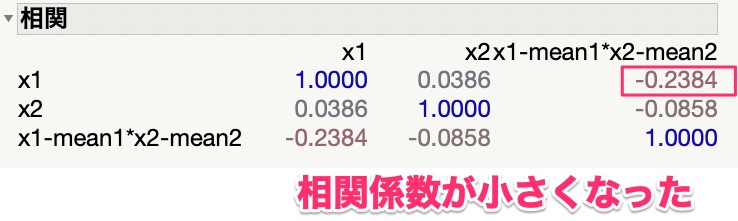
元の相関係数と比べて、かなり相関係数が小さくなったことがわかります。
これぐらいでしたら、多重共線性を心配する必要もないですね。
まとめ
この記事では「重回帰分析での交互作用項は中心化したほうがいい?多重共線性の解消方法」としてお伝えしました。
- 重回帰分析で連続変数を含む交互作用項がある場合に勝手に中心化されることがある
- 中心化(センタリング)って何?
- 中心化することで本当に多重共線性の問題は解決する?
ということを理解していただいたのなら幸いです!
こちらの内容は動画でもお伝えしていますので、併せてご確認くださいませ!












コメント