相関係数とは？p値や有意差の解釈などを散布図を使ってわかりやすく！

この記事では、相関係数に関して散布図を使ってわかりやすく解説しています。

相関分析でのp値の意味や有意差に関する解釈もお伝えしています。

 

複数の変数（データ）がある場合の解析手法として、回帰分析を紹介しました。

そして回帰分析と同様、複数の変数がある場合の解析手法として、記事では相関を紹介します。

まずは、相関係数に関する基礎知識について。

そして、相関と回帰分析の違いについて解説。

最後に、相関係数を解釈するときのp値や有意差に関する注意点を解説します。

 

相関係数とは？散布図を見ながら基礎的な知識をわかりやすく

2つの変数間の相関を知るために用いる指標は、相関係数という値です。

相関係数は、以下のような４つの特徴を持っています。

 

1. 単位がない
2. -1から1までの実数である
3. 1に近いときは、2つの確率変数には正の相関があるといい、-1に近ければ負の相関があるという。0に近いときには相関が弱い
4. 直線関係の強さを表している。

 

相関係数の３つ目の特徴である「1に近いときは、2つの確率変数には正の相関があるといい、-1に近ければ負の相関があるという。0に近いときには相関が弱い」を図で示すと、以下のようになります。

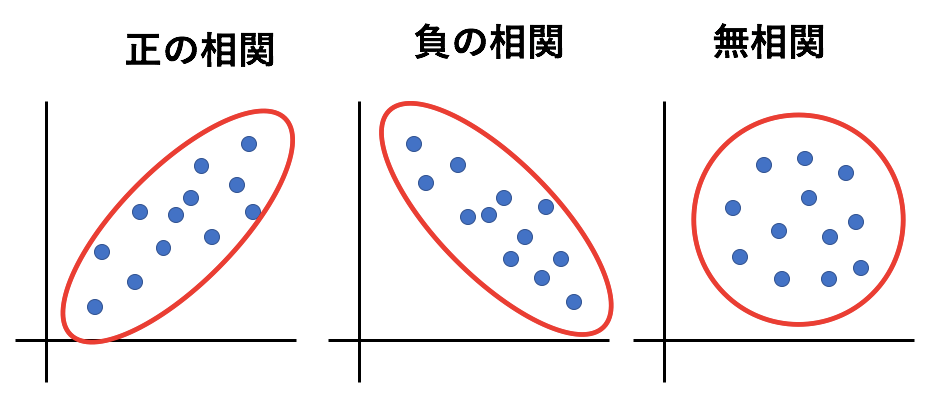
また、相関係数の4つ目の特徴である「直線関係の強さを表している」を図で説明すると、以下のようになります。

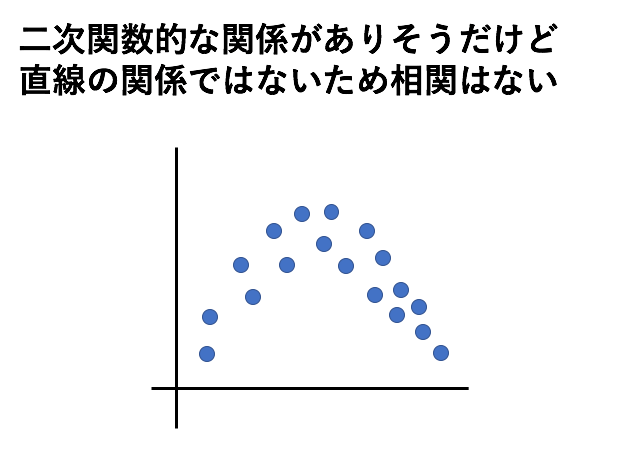
相関係数はあくまで「直線関係」を示しています。

そのため、二次関数的な関係があったとしても、相関係数は0に近くなります。

逆に言えば、相関係数が0に近い値であっても直線関係以外の関係を見いだせることがあるため、散布図を作成するなどして目視的に確認する事が重要です。

 

相関係数の性質：正の相関と負の相関の例

では、身近にある正の相関と負の相関の例を考えてみましょう。

一般的に、身長が高くなると体重が重くなります。

ということは、「身長」と「体重」の間には正の相関があります。

 

一方で、運動している習慣がある人は、生活習慣病の原因の一つである血圧が低い傾向にあります。

そのため例えば、「1週間の間に運動している時間」と「血圧」の間には負の相関があるということができます。

 

相関係数のp値や有意差はどんな意味があるか？

相関係数の分析でたまにこのような質問をいただく事があります。

「相関係数に関する検定で有意でなければ「相関が高い」とはいえないのでしょうか？」

あなたはどう思いますか？

 

なんとなく、正当なことを言っているように思えます。

それに、世間的には「相関係数の検定のp値が小さい方が相関が高い、すなわち関連が強いことを意味している」という誤解された解釈が広く認識されている気もします。

 

ですが、ちゃんと把握してもらう必要があるのは、次のことです。

 

「相関係数が大きいことと、相関係数の検定が有意であることは、切り離して考える」

 

なぜか。

基本に立ち返って考えてみましょう。

 

相関係数の帰無仮説と対立仮説は？

検定をするからには、帰無仮説と対立仮説があるはずです。

相関係数の検定に関する帰無仮説と対立仮説は何であるか、分かりますか？

答えは、以下の通りです。

 

 

つまり、相関係数のp値が0.05を下回った時に言えることは、「相関係数が０ではなさそうだ」ということだけです。

そのため、相関係数の検定に有意差があった時、「相関がないわけではない」という程度の意味しかなく、「相関が高い」ということは言えません。

 

相関係数のp値の意味と解釈は？

相関係数が0.1であっても、p＜0.05の場合があります。

一方で、相関係数が0.8であっても、p＞0.05の場合もあります。

 

この時、前者が「相関が高い」後者が「相関が低い」と言えるでしょうか？

言えないですよね。

 

なぜかというと、p値は相関係数の大小だけでなく、データの数に依存するからです。

このp値がデータ数に依存する、という性質はT検定などとも一緒です。

T検定では、２群の差の大きさだけでなく、データの数にも依存してp値が変わります。

そのような背景があるため、相関係数が高いことと相関係数の検定が有意であることは、切り離して考える必要があります。

 

相関分析と回帰はどう違う？

相関係数の特徴はわかりました。

ですが、ここで１つ疑問が。

２つの変数の比例関係を見る点では、相関も回帰分析も変わらないように感じます。

相関と回帰分析はどう違うでしょうか？

あなたは答えられますか？

 

実は、かなりの違いがあります。

相関は、２つの変数がどれくらい散らばっているかを表している解析になります。

一方で回帰分析は、一方の変数から他方の変数を予測するために最も都合の良い直線を引いています。

つまり、相関ではxとyが、どっちがどっちでもいいのです。

 

ピアソンの積率相関係数の数式を眺めてみます。

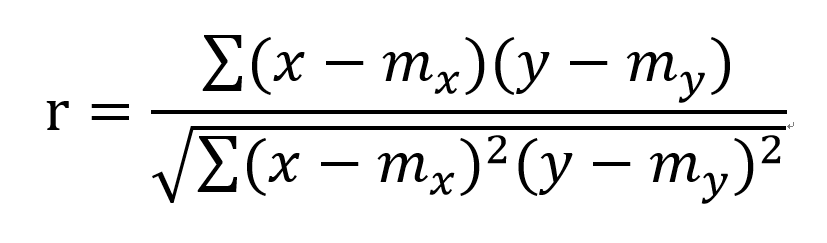
詳しいことは把握しなくても大丈夫です。

わかっていただきたいことはただ一つ。

この数式で、xとyを入れ替えたとしても、相関係数（r）の値は全く変わらないということです。

一方で回帰分析は、一方の変数（x）から他方の変数（y）を予測するために最も都合の良い直線を引いている、ということでした。

つまり、回帰分析ではどちらがxでどちらがyか、ということがとても重要になってくるのです。

 

相関係数に関する解釈の注意点

-1〜1の間しか取りうる数字がなく、しかもp値まで算出できるので、何かと便利に感じる相関係数。

しかし、相関係数にも解釈上の注意点があります。

 

相関係数の解釈注意点1：データ数が十分かどうか

統計全般に言える事ですが、データ数が十分でない場合には、相関係数の信頼性が低くなります。

例えばデータ数が5で、相関係数が0.7といった結果が出たとしても、その信頼性は高くありません。

ではどれぐらいのデータ数だったら十分なのか？という疑問もあるかと思いますが、それは一概には言えませんので、個々の判断になります。

 

相関係数の解釈注意点2：相関関係は因果関係を示すものではない

注意点の2つ目は、”相関関係は因果関係を示すものではない”という事です。

例えば、先ほどの負の相関の例で挙げた「1週間の間に運動している時間」と「血圧」の間には負の相関がある、ということを考えてみます。

一見すると、運動すれば血圧が下がる、というのは因果関係がありそうに思えます。

しかし逆を考えてみましょう。

血圧が正常である健康な人ほど、運動する余力があるので運動する時間が長い、という関係になっているかもしれませんよね。

そのため、あくまで相関関係は”何かしらの関係がある”ということしか示しておらず、”因果関係を示している”という事ではないので、注意してください。

因果関係を示しているかどうかを考察するには、データの取り方を工夫しなければなりません。

 

相関係数に関するまとめ

複数の変数を解析する手法の一つが相関。

相関係数は、以下の４つの性質がある。

相関係数のp値と、相関の大きさは切り離して考える。

 

動画でも相関係数の解説をしているので、記事を合わせてご確認くださいませ。