最小二乗平均（LSMean）とは？共分散分析で有意差がある場合とない場合のパターン

この記事では「最小二乗平均（LSMean）とは？共分散分析で有意差がある場合とない場合のパターン」としてお伝えします。

論文を読んでいると最小二乗平均（LSMean）という単語が出てくる場合がありますよね。

最小二乗平均を知らない場合、普通の平均値と何が違うの？と疑問に思うかなと思います。

そのためこの記事では

• 最小二乗平均値と普通の平均値（算術平均値）と何が違うのか？
• 最小二乗平均値を用いた解析である共分散分析の例
• 共分散分析で有意差がある場合とない場合のパターンについて解釈

を具体的にお伝えします！

 

最小二乗平均とは？算術平均と何が違う？

まずは最小二乗平均と算術平均との違いを整理していきましょう！

 

算術平均値とは？

算術平均値とは、皆さんが日ごろから使っている”平均値”と同じ意味となります（それほど多くはないと思いますが”相加平均値”という用語が使われることもあるようです）。

例えばある3つの値1、2、3があるとしましょう。

その算術平均値は、(1+2+3)/3と計算して、2となります。

算術平均値のよくある使い方としては、ある集団での代表的な値を示すために用いられます。具体的には、ある学校に所属する学生の身長などが挙げられますね。

いわゆる量的データ（連続量）に対する「要約統計量」を算出する際には算術平均値が用いられます。

 

最小二乗平均値とは？

では、最小二乗平均値とはなんでしょうか。

英語ではLS Mean (Least Square Mean)と表記され、個人的な印象では”最小二乗平均値”よりも”LS Mean”や”LSM”の用語を用いることの方が多いです。

さて、ここで回帰分析を既に勉強した方であれば、”最小二乗”という用語にピンときたかもしれません。

簡単に説明しますと、最小二乗平均値とは最小二乗法により求められた（今回の説明では）直線上の”ある点”となります。

これでは分かりづらいと思いますので、具体的な例やイメージ図を用いながら説明していきましょう。

 

例えば以下のようなデータがあったとして、これからYの最小二乗平均値を求めたいと思います。

X	Y
1	10
1	40
2	20
2	50

まずデータを散布図にしてみると、下記の図のようになります。

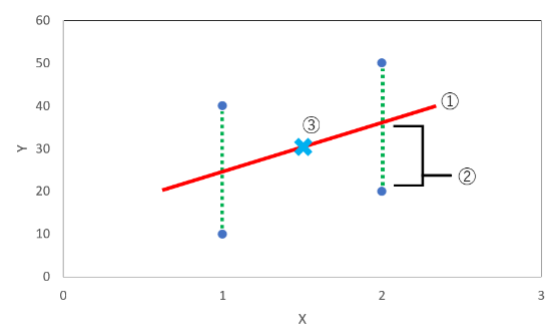
青い点が各データを示しています。

次に最小二乗法による直線（赤線）を求める方法ですが、非常に簡単に説明しますと上記の図の②（あるデータから直線までの距離）の合計値（今回の場合は4つ）が最小となるような直線（①）を探していくこととなります（具体的な計算方法は、ここでは省略させていただきます）。

先ほど最小二乗平均値とは、「最小二乗法により求められた直線上の”ある点”」と説明しました。

直線上の点は、直線上で文字通り無数に存在します。

ではどの点が最小二乗平均値なのでしょうか。

それは、”Xの平均値のときのYの値”が最小二乗平均値となります。

ですので上記の例では、Xの平均値（1+1+2+2）/4、つまりXが1.5のときのYの値30（図の③）が最小二乗平均値となります。

 

算術平均値と最小二乗平均値の同じところと違うところ

算術平均値と最小二乗平均値のそれぞれがわかったところで、算術平均値と最小二乗平均値同じところと違うところについて説明していきます。

先ほど最小二乗平均値の説明の箇所で”最小二乗法”という用語が出てきました。

普段私たちは意識していないかもしれませんが、算術平均値も最小二乗法を用いて算出することができます。

例えば以下の通り、Yだけのデータがあったとします。

Y

10

40

20

50

 

この時算出する算術平均値とは、言い換えれば「最小二乗法により求められた”ある点”（以下の図の青色の×）」となります。

最小二乗平均値との違いは、「直線上の”ある点”」の”直線上”という文言の有無でしかありません。

では、「直線上のある点」と只の「ある点」との違いとは何でしょうか？

中学生の時、直線を1次関数でY=aX + bのように表現できると習ったかと思います（YとXは変数（変化する値）、aとｂは決まった値）。

”ある点”を定数と読み替えるとY=bと表現することができ、この式は、1次関数Y=aX + bのaが0（つまり傾きが0）であった場合と考えることが出来ます。

 

以上をまとめますと、算術平均値と最小二乗平均値の同じところは、共に最小二乗法により求めることができるということです。

そして最小二乗法を用いる際に直線（Y = aX + b）を用いるか、それとも定数（Y = b）を用いるかが両者の違いとなります。

 

 

最小二乗平均値が用いられる解析手法の例

最小二乗平均値が用いられる解析手法として、共分散分析（ANCOVA：Analysis of Co-Variance）があります。

さて、共分散分析を簡単に説明すると、回帰分析と分散分析を併せた分析方法です。

交絡因子を調整した2グループのアウトカム（ある値）の違いを解析したい場合に良く用いられます。

 

例えば以下の通りのデータがあったとして、A剤グループとB剤グループとの間でYの値に違いがあるか知りたいとします。

X	Y		Yの 平均値
	A剤グループ	B剤グループ
1	1		2.75
2	3
3	2
4	5
5		5	6.50
6		7
7		6
8		8

Yの算術平均値は通りそれぞれのグループで2.75と6.50であり、グループ間でY値に違いがありそうです。

次にデータを散布図にしてみました。

そうすると、Y値に違いがありそうであるのと同時に、Xの値もグループ間で違いがありそうです。

こうなると、Y値の違いが、薬剤の違いなのか、X値の違いなのか区別できません。

何とかして”もしXの値がグループ間で同じであった場合の”A剤とB剤グループ間のY値の違いを調べることはできないだろうか？

そのような場合、共分散分析が使えます。

まずグループごとに最小二乗法を用いて直線を求めます。

次に、繰り返し出てくる「直線上の”ある点”」を求めるのですが、共分散分析の場合はちょっと異なり、”便宜的に”A剤とB剤全体の平均値（今回の例では4.5）におけるYの値となります。

つまり、A剤とB剤でぞれぞれ下記の図の水色と緑色の×印の箇所となります。

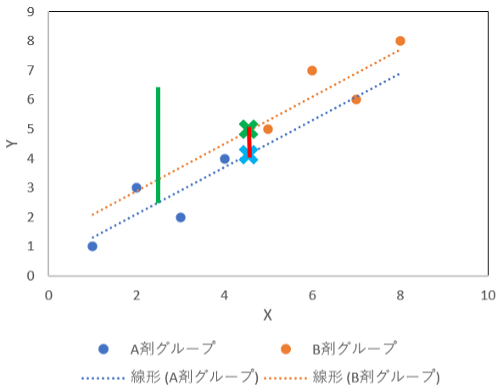
最後に×印の差（赤線）を調べます。

するとYの算術平均値の差（図の緑線）よりも、最小二乗平均値の差（図の赤線）の方が小さくなり、A剤とB剤グループとでのY値の違いは大きくないように思えます。

 

共分散分析を用いるための前提条件・注意点

共分散分析は、グループぞれぞれの最小二乗平均値を求めてその差を解析する方法ということがわかったかなと思います。

この方法を言い換えると、グループ間でＹ値以外の値の分布（今回の例ではＸ）に違いがある時、その違いを調整してＹ値を比較することができる非常に強力な解析方法です。

ですがこの方法を用いる場合には、それぞれのグループで決定した直線が平行であることが大前提の解析方法となります。

例えば以下の図では、A剤グループとB剤グループそれぞれの直線は明らかに平行ではありません。

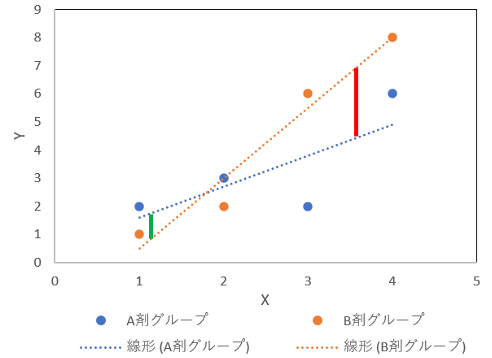
X値が高い箇所では、A剤グループの方でY値が高い（図の赤線）のですが、X値が低い箇所ではB剤グループの方でY値が高く（図の緑線）なっています。

この様な場合、Xと群との間に交互作用があると言い、共分散分析を使用する前提に反していることになります。

ただし、実データで直線が並行になることは稀であり、少なからず傾きが違うはずです。

なのでどこまでの傾きならOKなのか、という程度問題にはなります。

 

最小二乗平均を用いた共分散分析での有意差がある場合とない場合の解釈について

共分散分析を用いた解析結果の解釈について説明していきます。

共分散分析での結果と算術平均値を用いた場合での結果を組み合わせると4パターンを取りうることが予想できます（下表のa、b、c、d）。

		算術平均値の差
		なし	あり
共分散分析 （最小二乗平均値の差）	なし	a	b
	あり	c	d

これからそれぞれのパターンごとの解釈の仕方について説明していきます。

まずパターンaの一例としては以下のような図が挙げられます。

このような場合は、薬剤グループ間でＹ値の違いは見つからなかったとの結論で問題ないと考えられます。

 

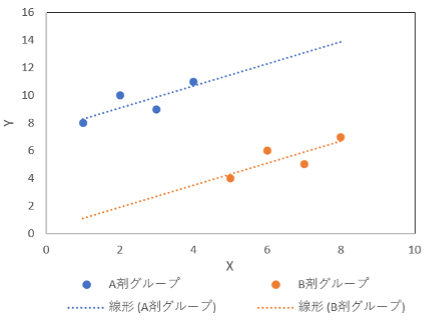
次にパターンbの場合は以下の通りで、グループ間のＹ値の差は薬剤の違いが起因しているのではなく、X値の違いであるという解釈が妥当となります。

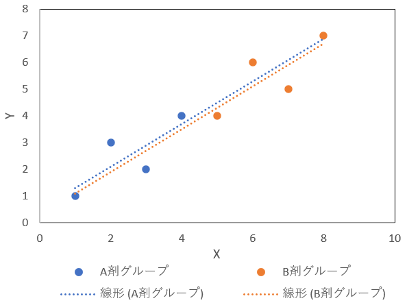
パターンcの場合は、X値の違いにより薬剤の違いが消えてしまっていると解釈できます。

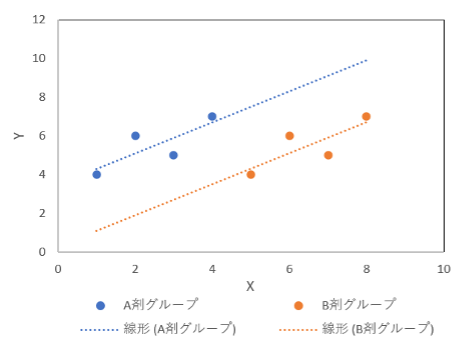
最後にパターンdの場合は、X値の違いを取り除いたとしても、グループ間で差は認められるという解釈が成り立ちます。

 

まとめ

いかがでしたか？

この記事では「最小二乗平均（LSMean）とは？共分散分析で有意差がある場合とない場合のパターン」としてお伝えしました。

• 最小二乗平均値と普通の平均値（算術平均値）と何が違うのか？
• 最小二乗平均値を用いた解析である共分散分析の例
• 共分散分析で有意差がある場合とない場合のパターンについて解釈

が理解できたのなら幸いです！