級内相関係数(ICC:intraclass correlation coefficients)は、研究で何か計測を行う時にしばしば登場する指標です。
論文でも「ICC(1,1)が〜〜で」というような記載をしばしば見かけます。
でも級内相関係数って一体何なのか、気になっている方も多いのではないでしょうか？
相関係数は知っているけど、級内相関係数ってなんだろう。。
本記事ではそんな方のため、級内相関係数の意味や計算方法をなるべくわかりやすく解説していきます。
数学が苦手な方でも大丈夫なのようにわかりやすくしてあるので、安心して下さいね！
Contents
級内相関係数とは？ICCをわかりやすく解説！
まずは級内相関係数の概要を把握していきましょう！
級内相関係数とは？
級内相関係数(ICC)とは、連続量である検査の信頼性を確かめる指標です。
信頼性といっても以下の2つの意味があります。
検者内信頼性：同じ人が何回検査をしても同じ値が出る
検者間信頼性：誰が検査をしても同じ値が出る
検者内信頼性が低い検査は毎回検査するたびに違う値が出てしまいますし、検者間信頼性が低い検査は、検査者によって違う値が出てしまいます。
どちらが低くても困りますよね。
信頼性が高い検査とは、”誰が検査を何回とっても、常に同じ値が出る検査”のことです。
級内相関係数はその検査の信頼性が高いかどうか確かめる指標、というわけです。
ちなみに、カテゴリカル変数の検査の一致度合いはカッパ係数が用いられます。
級内相関係数の種類
級内相関係数はICC(1,1)というように2種類の数字を使って表現します。
この2つの数字は一体何なのでしょうか？
1つ目の数字は”何の信頼性か”を示しています。
1から3まで3種類あり、以下の意味をもっています。
ICC(1,~)：検者内信頼性
ICC(2,~)：検者間信頼性
ICC(3,~)：相対一致検者間信頼性
主に使うのはICC(1,~)とICC(2,~)で、最初に説明した検者内信頼性と検者間信頼性を示します。
ICC(3,~)はほとんど使われませんが、ICC(2,~)との違いを簡単な例を使って説明しますね。
興味のない方は読み飛ばしても構いません。
例えば身長を測る係の人が3人いるとしましょう。
そのうち1人はバーを力強く押し付けてくるため実際の身長より1cm低く測定してきます。
ですので同じ人を測定しても、その人だけは常に1cm低い検査結果になります。
このようなケースだと、ICC(2,~)だと信頼性が低くなりますが、ICC(3,~)だと信頼性は下がりません。
ただこのようなケースはほとんどありませんので、ICC(3,~)が使われることはほとんどありません。
まずはICC(1,~)なら検者内、ICC(2,~)なら検者間の信頼性の指標だと覚えておきましょう。
次に2つ目の数字の意味を解説します。
2つ目の数字は”同じ検者が同じ人に同じ計測を何回したか”を示します。
例えば1人の検者が1人の被験者に3回ずつ測定を行い、その平均値を使って級内相関係数を求めた場合、ICC(1,3)となります。
級内相関係数の解釈
ICCは0~1の値をとり、基本的に0.7以上であれば信頼性があると判定します。
ただ0.7という基準に理論的根拠はないため、あくまで目安として捉えるようにしましょう。
級内相関係数の求め方をエクセルで解説！
級内相関係数はエクセルでも計算できますので、その具体例を解説します！
級内相関係数の計算式
ICC(1,1)の計算式は以下のようになります。
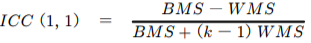
- BMS=サンプル間の変動
- WMS=”測定ごとの変動”＋”誤差”
- k=測定回数
このままだとよく分かりませんね(^^;)
この計算式を解説すると数学の授業になってしまうので、ひとまず「こんな計算式なのね」と認識していただければ十分です。
後は実際にエクセルで級内相関係数を求めながら理解していきましょう！
級内相関係数をエクセルで計算するためのデータの準備
具体例を使って級内相関係数を計算してみましょう。
ある検者が10人の被験者の身長を2回ずつ測定したとしましょう。
この時の測定の検者内信頼性を級内相関係数を使って確認します。
データはこのようにまとめました。
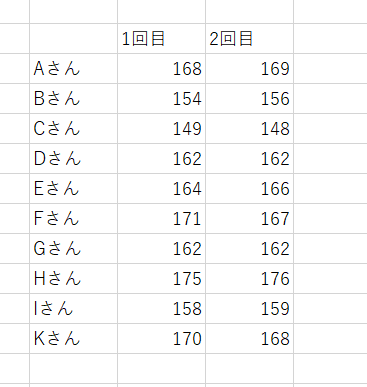
2回の測定のばらつき(変動)が少なければ少ないほどこの場合、級内相関係数は高くなるはずです。
BMS,WMSを計算
厄介なBMSとWMSの計算ですが、実は簡単に計算する方法があります。
まずはエクセルのデータ分析機能を使って、”繰り返しのない二元配置分散分析”という分析をしてみましょう。
エクセルのデータタブを開くとデータ分析という項目があります。（ない方はアドインで追加しましょう）
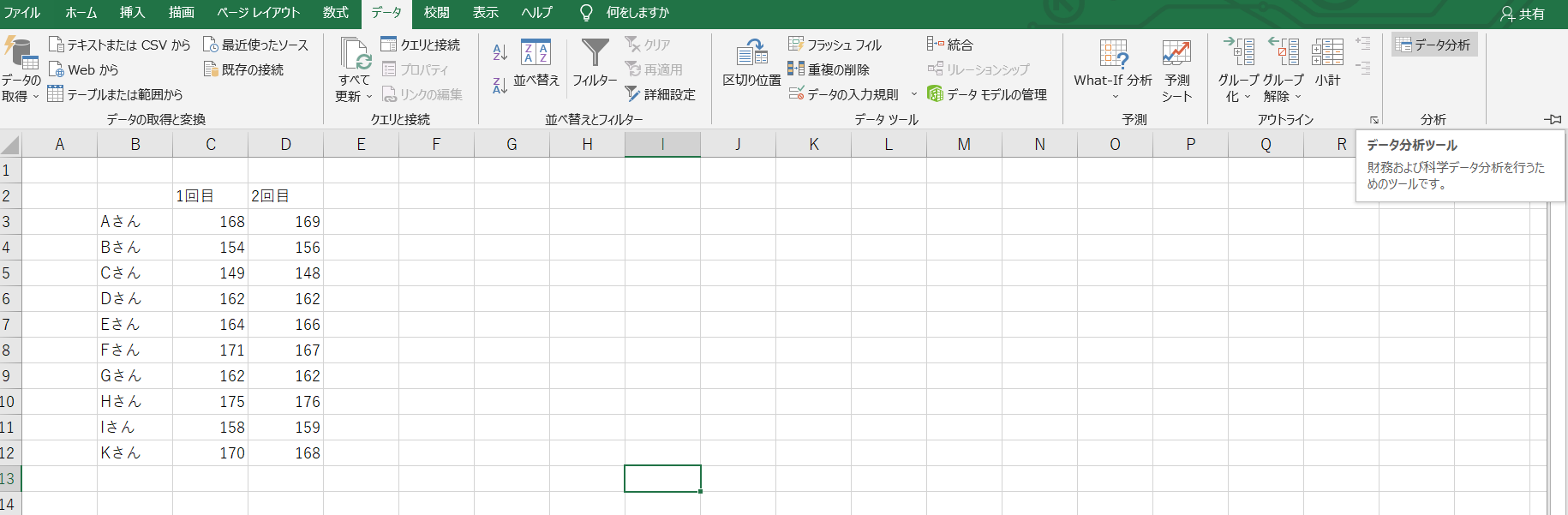
この”データ分析”をクリックして”繰り返しのない二元配置分散分析”を選択、先ほどの表をデータ範囲に指定しましょう。
実行すると以下の表が出力されます。
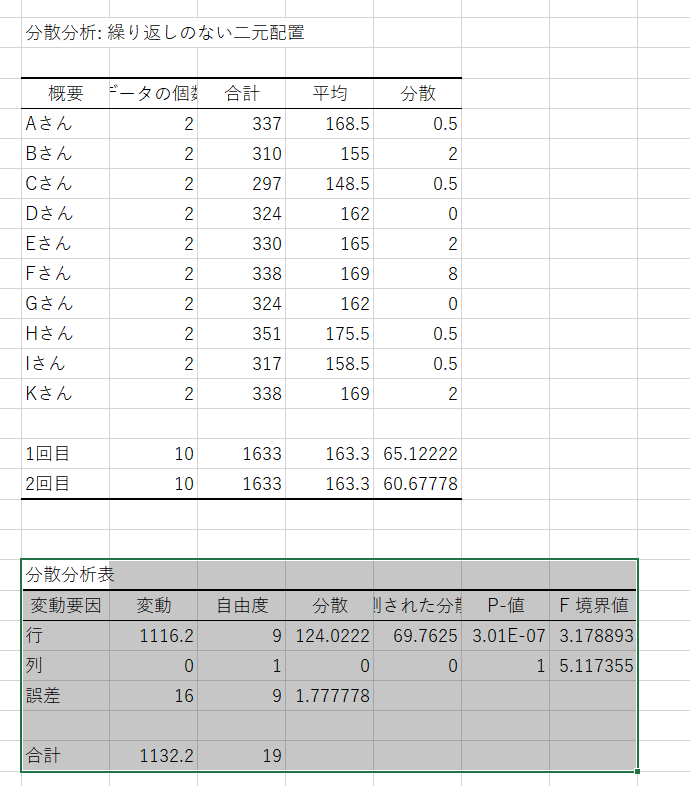
下の”分散分析表”を使えばBMSとWMSを簡単に算出できます。
BMS=”行”の分散
WMS=(“列”の変動 + “誤差”の変動) / (“列”の自由度 + “誤差”の自由度)
k=2(今回は2回測定しているため）
エクセルの数式は以下のようになります。
級内相関係数を算出
BMS,WMS,kが算出できたので、後は最初に説明した数式を組み込むだけです。
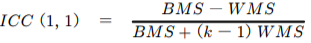
実際にエクセルに入力すると以下のようになります。
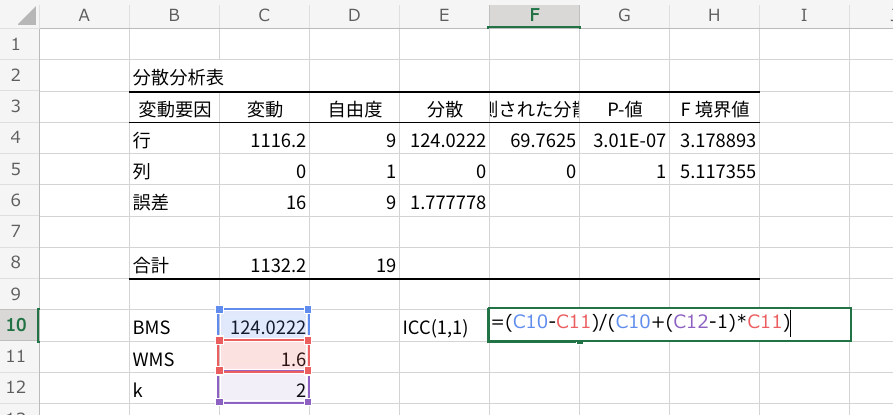
最後にEnterキーで級内相関係数を算出できます。
ICC(1,1)=0.97ですので、検者内信頼性は高いと言えそうです。
ちなみに測定ごとのデータの変動を反映するWMSの値を大きくすると結果はこのように変わります。
このように測定ごとのデータの変動(ばらつき)が大きいほどICCも下がります。
いかがでしょうか？
計算式で見ると難しいですが、エクセルの計算自体はそこまで難しいわけではありません。
エクセルでICCを算出する際は、是非参考にしてくださいね。
まとめ
最後におさらいをしましょう。
- 級内相関係数とは検査の信頼性を示す指標
- ICC(1,~)は検者内信頼性、ICC(2,~)は検者間信頼性を示す
- ICC(~,n)は同じ被験者にn回測定を繰り返し、その平均値を使って算出する
- ICCは0~1の値をとり、基本的に0.7以上であれば信頼性があると判定する
級内相関係数はエビデンスの乏しい検査方法を採用する時に必ず必要になってきます。
級内相関係数を計算していないためにリジェクトされるケースもよくあります。
そのため少し難しいところもありますが、この記事の内容を是非覚えておいて下さいね！
最後までお読みいただきありがとうございました。
第1章：臨床研究ではなぜ統計が必要なのか？計画することの重要性
第2章：研究目的をどれだけ明確にできるのかが重要
第3章：p値で結果が左右される時代は終わりました
第4章：多くの人が統計を苦手にする理由
第5章：統計を使えるようになるために今日から何をすれば良いか？
第6章：統計を学ぶために重要な環境
もしあなたがこれまでに、何とか統計をマスターしようと散々苦労し、何冊もの統計の本を読み、セミナーに参加してみたのに、それでも統計が苦手なら…
私からプレゼントする内容は、あなたがずっと待ちわびていたものです。
