自由度調整済み決定係数とは？意味や解釈、活用法を解説！

2024年8月14日2024年8月15日

重回帰分析を扱う際に必要な知識として、自由度調整済み決定係数という言葉があります。

文字通り決定係数を自由度で調整したものなのですが、

「自由度って一体何？」
「なんで調整してるの？」
「普通の決定係数と何が違うの？」

といった疑問を持っている方も多いのではないでしょうか？

本記事では自由度調整済み決定係数の意味や目安、解釈について解説します。

初心者の方でも大丈夫なようになるべくわかりやすく説明していきますね！

＞＞もう統計で悩むのは終わりにしませんか？

↑期間・数量限定で無料プレゼント中！

自由度調整済み決定係数とはどんな意味を持つ？

自由度調整済み決定係数がどんな意味を持つのか、まずは学んでいきましょう！

そもそも重回帰分析における決定係数とは？

決定係数とは、”重回帰分析の結果がデータにどれくらい当てはまっているか”を示す指標です。

もう少し噛み砕くと、分析結果の妥当性を表す指標の一つです。

たとえば”血圧に影響する因子を重回帰分析で探す”ことになったとしましょう。

分析に使う変数に肥満度などの血圧に影響しやすい因子が含まれていれば、決定係数は高くなります。

反対に血圧に影響する因子がまったく入っていなければ、決定係数は低くなります。

つまり決定係数を見れば、重回帰分析で抽出された因子がどれくらい血圧に影響にしているのか知ることができます。

以上の理由から決定係数は”分析結果の当てはまり具合”を表すものとして解釈されます。

決定係数の詳細は、こちらの記事でも解説しています。

自由度調整済み決定係数とは？

決定係数が分かったところで、では、自由度調整済み決定係数とはなんでしょうか？

自由度調整済み決定係数とは、重回帰分析で抽出する変数の数に応じて決定係数が小さく補正されるようにしたものです。

なぜそのような補正が必要なのでしょうか？　

実は決定係数には、変数の数が多ければ多いほど値が高くなるという性質があります。

そのため全く関係のない変数ですら使えば使うほど決定係数が上がっていってしまいます。

極端な話だと、目的変数と関係の強い3つの変数を使った重回帰分析と全く関係ない変数を10000個使った重回帰分析の決定係数が同じになる可能性があるということです。

本来少ない変数の方がいいですから、この欠点はなんとかしないといけませんよね。

そのため変数を使えば使うほど決定係数が高くなるという欠点を改善したのが自由度調整済み決定係数というわけです。

自由度調整済み決定係数の導出

自由度調整済み決定係数の意味が分かったところで、自由度の意味や計算式について説明していきましょう。

なお、ここではわかりやすいように数式ではなく言葉を使って計算式をお伝えします。

決定係数の計算式は以下のようになります。

変動とはデータのばらつき具合を示しており、残差とは重回帰分析の予測値からのデータのズレ具合を示します。

重回帰分析の精度が上がれば上がるほど残差は小さくなりますので、決定係数も上がるというわけです。

次に自由度調整済み決定係数は以下のようになります。

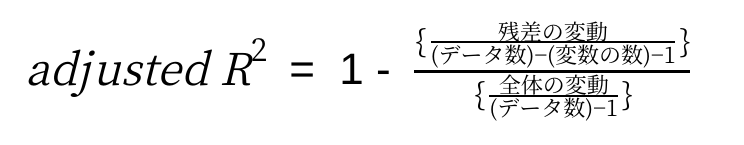
先ほどの変動を”データ数”や”変数の数”で割っていますが、これが”自由度”です。

自由度は少々難しい概念なのですが、自由度調整済み決定係数を理解する上では”データ数と変数の数を反映するもの”と認識しておけばOKです。

話を自由度調整済み決定係数に戻しましょう。

少しややこしい式になってきましたが、”変数の数”が計算式に組み込まれたことだけ知っておけば大丈夫です。

この式だと、変数の数が多ければ多いほど決定係数が下がることになります。

この調整のおかげで自由度調整済み決定係数は、適切な変数だけを使わないと上がらない仕組みになっています。

自由度調整済み決定係数の結果の解釈

自由度調整済み決定係数がどのような性質を持ち、どんな計算で導き出されたのかが分かったところで、結果の解釈について解説しますね！

自由度調整済み決定係数に目安となる数値はある？

自由度調整済み決定係数に「これ以上ならいいよ！」という絶対的な目安はありません。

相関係数や決定係数にも絶対的な目安がないのと同じですね。

あくまで相対的な評価に使う値として認識しましょう。

しかし以下の点は覚えておくと良いかなと思います。

基本的に0~1の値をとる(一部例外あり)
1変数を使用した単回帰分析では相関係数を二乗した値が決定係数になる
医療統計では0.5を超えれば優秀とみなされることが多い

特に②が重要で、単回帰分析の場合は相関係数が0.7になる変数に対して決定係数は0.49です。

相関係数が0.7というと結構関係が強い印象ですが、それでようやく0.49です。（自由度で調整すると更に低くなります）

この点を踏まえると、「決定係数が0.5を超えれば優秀」という解釈は妥当だといえます。

ただし繰り返しますが、この基準は絶対ではありません。

“筋肉量”と”筋力”のように、明らかに関係が強そうな分析で決定係数が0.5だと優秀だとは言えませんよね。

結局は分析内容次第であることを覚えておきましょう。

ちなみに、決定係数のルートであるRは、重相関係数とも呼ばれています。

重相関係数に関してはこちらの記事をご覧ください。

自由度調整済み決定係数の活用例

自由度調整済み決定係数が活用できるの以下の例です。

異なる変数を使った分析結果を比較したい(どのモデルが妥当か判別できる)
変数をいくつ使うか調整したい

①に関してはここまで説明した通りです。

たまに同じ目的変数をいろいろな因子の組み合わせで分析したいときがありますよね。

この時に自由度調整済み決定係数を使えば変数の数に左右されずに分析結果の妥当性を評価できます。

自由度調整済み決定係数の高いモデルのほうが、その目的変数をよく説明していると簡単に解釈ができます。

②は因子の数が多すぎて、どの因子を分析に使うべきか絞りたい時に使います。

すでに説明した通り決定係数は変数が多ければ多いほど高くなるため、全因子を使ったほうがよいということになってしまいます。

自由度調整済み決定係数ならば目的変数の関連の低い因子を入れると値が下がるため、関係ない因子を消すことができます。

この考え方はステップワイズ法と呼ばれる方法です。

ステップワイズ法にはAICという指標が使われることが多いのですが、自由度調整済み決定係数でも同じことができます。

ステップワイズ法について詳しく知りたい方は、こちらの記事をご覧ください。

自由度調整済み決定係数でマイナスになることある？

自由度調整済み決定係数はマイナスになることがあります。

具体的には、変数をたくさん使っているのに決定係数が低いケースではマイナスになります。

先程の計算式からなぜマイナスになるのか考えていきましょう。

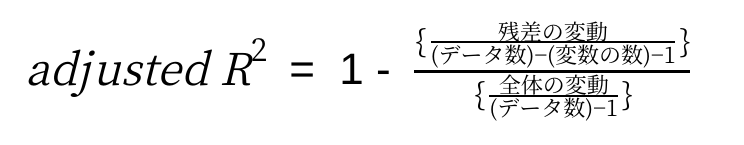
この式をみてもらうとわかるように、一番右側の分数の部分が1以上の時に調整済み決定係数はマイナスになります。

そして分数が1以上になるのは、分子が分母より大きい値の時です。

目的変数と関係ない変数ばかり使った分析では、”全体の変動”と”残差の変動”はほとんど同じ値になります。

次に”自由度“を比較すると、分子のほうが”変数の数”を余計に引いています。

そのため分子の方が分母よりも大きな値になります。

この結果、分子が分母よりも大きくなり調整済み決定係数がマイナスになってしまうのです。

通常の意味のある分析であれば”全体の変動”より”残差の変動”は小さいので、いくら自由度で調整してもマイナスにはなりません。

でも極端に目的変数と関係ない変数ばかりで分析すると、マイナスになってしまいます。

＞＞もう統計で悩むのは終わりにしませんか？

↑1万人以上の医療従事者が購読中

Rで決定係数と自由度調整済み決定係数を深く理解する

では実際に、サンプルデータを用いて決定係数と自由度調整済み決定係数の違いを深く理解していきます。

datariumというパッケージに含まれるmarketingというサンプルデータを使います。

サンプルデータを用いて、下記の解析を実施します。

sales（売り上げ）を目的変数として、youtube（youtubeの広告費）のみを説明変数とした回帰分析
sales（売り上げ）を目的変数として、youtube（youtubeの広告費）とfacebook（facebookの広告費）を説明変数とした回帰分析
sales（売り上げ）を目的変数として、youtube（youtubeの広告費）とfacebook（facebookの広告費）とnewspaper（newspaperの広告費）を説明変数とした回帰分析

#1度だけ実施する。過去にインストールしたことがあれば実行しなくてOK
install.packages("datarium")
install.packages("dplyr")

# パッケージの読み込み
library(dplyr)

# データの読み込み
data("marketing", package = "datarium")

# データの確認
head(marketing, 3)

# youtubeのみを説明変数とした回帰分析
fit <- lm(sales ~ youtube, data = marketing)

#解析結果の確認
summary(fit)


# youtubeとfacebookを説明変数とした回帰分析
fit2 <- lm(sales ~ youtube + facebook, data = marketing)

#解析結果の確認
summary(fit2)


# youtubeとfacebookとnewspaperを説明変数とした回帰分析
fit3 <- lm(sales ~ youtube + facebook + newspaper, data = marketing)

#解析結果の確認
summary(fit3)

上記のプログラムを実施すると、下記のような決定係数（Multiple R-squared）と自由度調整済み決定係数（Adjusted R-squared）が得られました。

説明変数	決定係数	自由度調整済み決定係数
Youtubeのみ	0.6119	0.6099
Youtubeとfacebookの2つ	0.8972	0.8962
Youtubeとfacebookとnewspaperの3つ	0.8972	0.8956

決定係数は説明変数を入れれば入れるほど大きくなります（少なくとも小さくはならない）が、自由度調整済み決定係数は、説明変数を増やした場合に小さくなることがあります。

Youtubeとfacebookの2つを説明変数とした解析より、Youtubeとfacebookとnewspaperの3つを説明変数とした解析の方が自由度調整済み決定係数が小さくなっていることがわかります。

そのため上記3つの解析の中では、売上にはYoutubeとfacebookの2つの媒体に対して広告費をかけることが最適な可能性がある、ということになります。