医療系全般で、量的データ（連続データ）のアウトカムに関するリスク因子の検討や因果推定のために、回帰分析ないしは重回帰分析がよく行われます。
回帰分析を行うと、どのようなソフトウェアでも決定係数（R二乗値、寄与率）というものが出力されます。
決定係数（R二乗値、寄与率）は回帰分析を評価する上で重要な指標であり
論文等で回帰分析結果を表示する場合には、決定係数の表記は必須と言って過言ではありません。
この決定係数とはいったい何なのか。
決定係数をわかりやすく解説していきます。
決定係数（R二乗値、寄与率）とはどんな指標？
回帰分析、特に2つ以上の説明変数を投入する重回帰分析を行った場合、分析の良し悪しを評価する視点は大きく分けて2つあります。
ひとつは、個々の説明変数が目的変数に与える影響に有意差が認められるどうかという視点です。
これは、（偏）回帰係数の仮説検定を通して確認されます。
医療系の研究において、回帰分析を行う場合、特定の要因の影響の有無の確認が主目的であることが多いのでこちらを中心に議論が進んでいくことが多いと思います。
もう一つは、投入した説明変数によって、目的変数が十分説明されているかという視点です。
回帰モデルがどの程度適合しているか、当てはまりが良いか、という言い方がなされることもあります。
「投入した説明変数によって、目的変数が十分説明されているか」という視点から回帰分析を評価したものが決定係数になります。
決定係数（寄与率）が示している「目的変数が説明変数で十分説明されている」とは？
下のグラフは全身骨密度に与える加齢の影響を調べるために行った回帰分析の結果です。
被験者50名ずつの2つのスタディについて、
- 目的変数：全身骨密度
- 説明変数：年齢
として、それぞれ回帰分析を行っています。
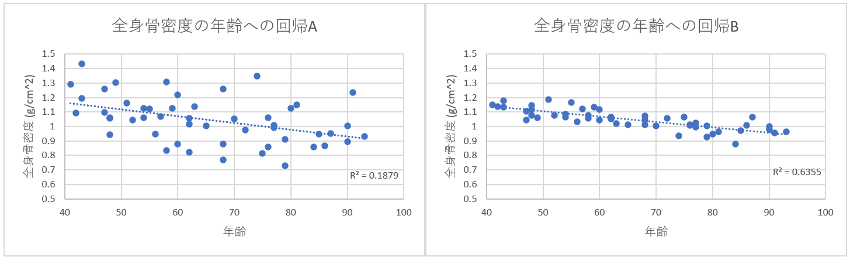
A, Bいずれの回帰分析も右下がりになっていますので、加齢とともに全身骨密度が低下しているのがわかります。
回帰係数はいずれもマイナスの値であり、年齢に対する偏回帰係数の仮説検定を行うと、どちらも統計的に有意です。
すなわち、加齢とともに全身骨密度が低下していくことが検証されています。
個々の説明変数が目的変数に与える影響に有意性が認められるどうかという視点からすると、どちらも意味のある回帰分析ということになるかと思います。
しかし、投入した説明変数によって、目的変数が十分説明されているかという視点からするとどうでしょうか。
Aのほうは、各被験者を表す点が回帰直線から大きくバラついているのに対し、Bのほうは回帰直線にまとわりついているように見えませんか。
- A, Bいずれも加齢とともに全身骨密度の低下傾向は見られますが
- Aは同じ年齢であっても全身骨密度が比較的バラついているのに対し、
- Bは同じ年齢の被験者は概ね同じような全身骨密度の値となっています。
これは、Aのほうは年齢以外に全身骨密度に影響を与える他の要因があることを示唆し、Bのほうは年齢のみで全身骨密度を十分説明できることが示唆されています。
この違いを数値化したものが決定係数になります。
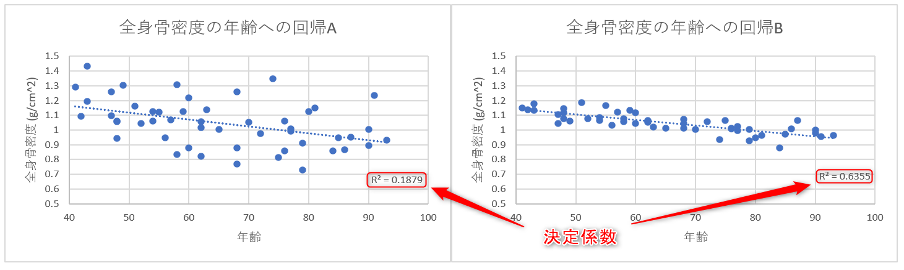
Aの回帰の決定係数は0.1879であるのに対し、Bの回帰の決定係数は0.6355と高い値ですね。
つまり、AよりもBのほうがより適合していることを表しています。
決定係数とはどんな意味を持つの？
決定係数は、目的変数が十分に説明されているかどうかを数値化したものですが、具体的にはどのように計算されているのでしょうか。
決定係数の背景には以下のような発想があります。
説明変数が目的変数に何ら寄与していないという前提で、目的変数は定数である平均値（期待値）から誤差を伴ってバラついているとする「最単純モデル」と回帰分析によって推定された「回帰直線」を比較する
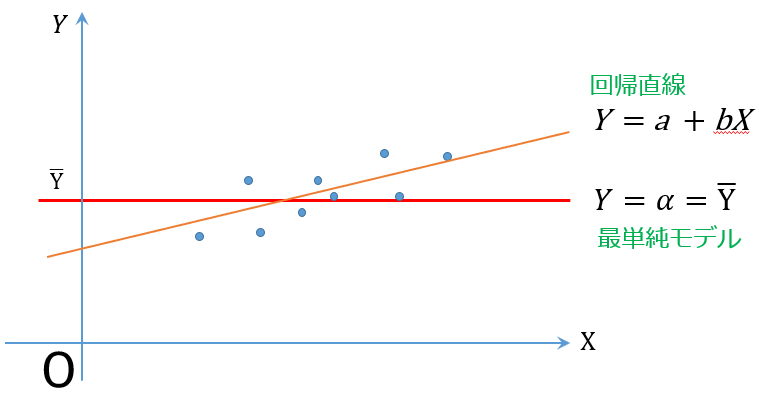
決定係数の定義
決定係数は、回帰分析が残差平方和を最小化する係数を推定量とすることから「最単純モデル」の残差平方和と「回帰直線」の残差平方和を比較することで、回帰分析を評価しようとします。
数学的には、決定係数は「回帰直線」の残差平方和と「最単純モデル」の残差平方和の比を1から引いた値として定義されます。
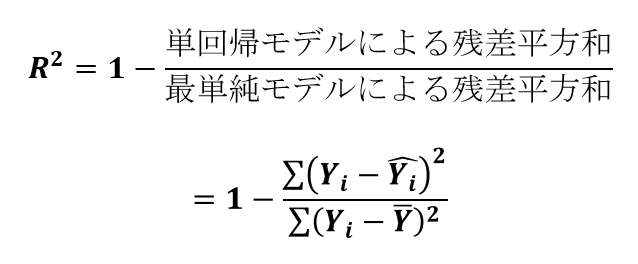
決定係数が高いとどんな意味で低いとどんな意味？
決定係数は上の定義により、比率（割合）としての意味合いを持つため、0以上1以下の値となります。
決定係数の値が高い場合の意味
冒頭で示した、全身骨密度の年齢への回帰Bのように、説明変数が目的変数を十分に説明できている、すなわち、回帰分析の当てはまりが良いとき。
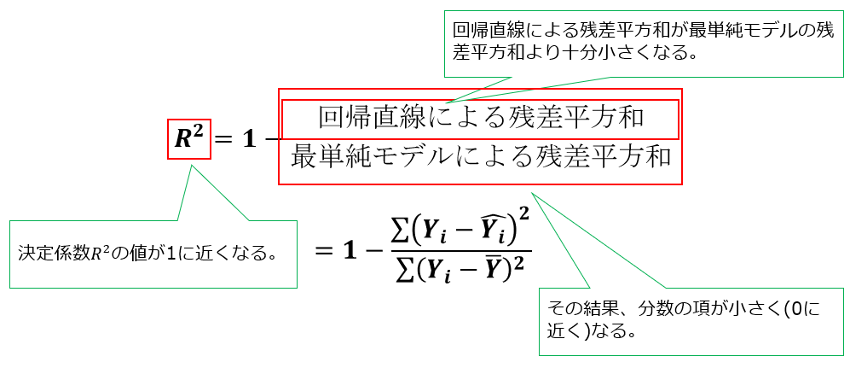
ということになり、決定係数が高い値となります。
つまりざっくり言うと、最単純モデルを考えたときの残差よりも、回帰直線を考えたときの残差の方が小さくなるので、決定係数が高くなる、ということです。
決定係数が1に近い高い値のとき、説明変数は目的変数を十分に説明できていると言えます。
決定係数の値が低い場合の意味
冒頭で示した、全身骨密度の年齢への回帰Aのように、説明変数が目的変数を十分に説明できているとは言えない、すなわち、回帰分析の当てはまりが悪いとき。
ということになり、決定係数が低い値となります。
つまりざっくり言うと、最単純モデルを考えたときの残差と、回帰直線を考えたときの残差はあまり変わらないので、決定係数が低くなる、ということです。
決定係数が0に近い低い値のとき、説明変数は目的変数を十分に説明できているとは言えません。
決定係数と相関係数の関係：目安はあるの？
相関係数はrと小文字で表現されるのに対して、決定係数は大文字のRの2乗と表現されます。
同じアルファベットが用いられるのは相関係数と決定係数の間に関係があるからです。
決定係数は定義の式を変形することで、目的変数と回帰式による目的変数の予測値との相関係数の2乗に一致することが確かめられます。
したがって、Rの2乗と表記しているのです。
こちらも参考にしていただければ。
決定係数の目安
決定係数は1に近いほど良くて、0に近いほど悪いということがわかりましたが、はたして目安はあるのでしょうか。
0.5を超えると当てはまりが良いとされることが多いですが、残念ながら絶対的な基準はありません。
ただ、決定係数が相関係数の二乗の関係にあるならば、「決定係数が0.5以上＝相関係数が0.7以上」ということになります。
相関係数が0.7以上というのは「強い相関がある」と一般的に言われている値ですよね。
ただ私の経験上、医療系のデータで相関係数が0.7以上あるような関係はそれほどないため、決定係数が0.5という基準もかなり厳しいのでは、と思います。
そのため、決定係数の使い方としては「これ以上の値だから説明能力が高い」という絶対的な使い方よりも、「AというモデルよりもBというモデルの方が説明能力が高い」という相対的な使い方の方が現実的ですね。
まとめ
決定係数は、回帰係数の仮説検定と並び、回帰分析の重要な評価指標です。
説明変数の具体的な影響の有意性とは別に、説明変数のもつ目的変数に対する説明力を数値化したものですので、分析全体の精度を確認することができます。
その意味合いをおさえつつ、論文等にはしっかり記載するようにしましょう。
なお、重回帰分析の場合には、決定係数を修正した「自由度調整済み決定係数」が用いられます。この話題はまた別の機会に解説したいと思います。
コメント
コメント一覧 （1件）
[…] 決定係数とは、”重回帰分析の結果がデータにどれくらい当てはまって… […]