この記事では「カッパ係数(k係数)とは?EZRでの一致度の求め方と解釈の注意点」としてお伝えします。
- カッパ係数ってそもそもどんな指標でどんな時に使えるの?
- カッパ係数をEZRで求める方法は?
- カッパ係数の結果の見方に注意点ある?
といったことがわかるようになりますよ!
カッパ係数(k係数)とは?

カッパ係数とは、質的データ(カテゴリカルデータ)に対して2つの検査結果の一致度合いを評価する指標のことです。
ちなみに、量的データ(連続量)に対して2つの検査結果の一致度合いを評価する指標は級内相関係数(ICC)ですね。
ということで、カッパ係数とはどんな指標なのかを、例を使って考えてみましょう。
例でカッパ係数を理解する
例えば、以下のような状況を設定してみます。
120人に対してAの検査とBの検査の2種類を実施する。
Aの検査とBの検査も、「陽性」か「陰性」の判定をする検査である。
その時に、Aの検査とBの検査の一致度合いを評価したい。
- Aの検査とBの検査の2種類を実施
- 検査結果はどちらも2値のカテゴリカルデータで判定される
- 一致度合いを評価したい
このような場合に、カッパ係数は有効です。
仮に120人の検査結果として、以下のような判定がなされたとします。
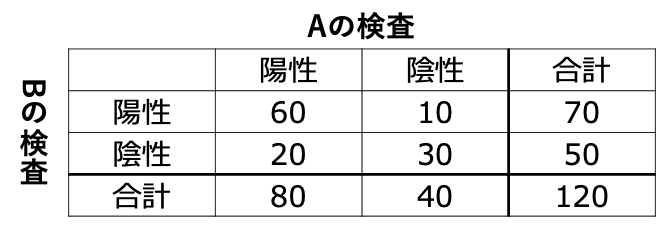
- Aの検査もBの検査も陽性である:60人
- Aの検査もBの検査も陰性である:30人
- Aの検査は陽性だがBの検査は陰性である:20人
- Aの検査は陰性だがBの検査は陽性である:10人
この場合のカッパ係数を考えます。
カッパ係数の考え方1:単純な一致度を計算
まず、単純に一致度を考えてみます。
単純な一致度というのは、(どちらも陽性の人数+どちらも陰性の人数)/合計の人数、で示されます。
これを上記の表に当てはめると、(60+30)/120=0.75。
カッパ係数の考え方2:単純な一致度に対して、たまたま一致したとみなされる割合と、本当に一致したとみなされる割合を分ける
単純な一致度は0.75でした。
しかしこの結果は、
- たまたま一致したとみなされる割合
- 本当に一致したとみなされる割合
の2つが混ざった結果である、という考え方をするのです。
じゃあ、たまたま一致したとみなされる割合は?というと以下の計算手順で求めます。
- 偶然に陽性となる割合:Aが陽性となる確率とBが陽性になる確率の積=80/120*70/120=0.389
- 偶然に陰性となる割合:Aが陰性となる確率とBが陰性になる確率の積=40/120*50/120=0.139
- 上記の二つを足す:0.389+0.139=0.528
では、今回の検査での偶然じゃなく一致した部分の割合は?というと、単純な一致度からたまたま一致したとみなされる割合を引けばいいので、
- 今回の検査での偶然じゃない部分の割合:0.75-0.528=0.222
となります。
カッパ係数の考え方3:理論上、本当に一致したとみなされる割合を求める
次に、理論上、Maxで本当に一致したとみなされる割合を求めます。
理論上、単純な一致度というのはMaxが100%です。
そのため、今回のデータでは理論上のMaxで本当に一致したとみなされる割合は
- 1-0.528=0.472
と計算できます。
カッパ係数の考え方4:今回のデータの本当に一致したとみなされる割合は、理論上Maxに対してどのぐらいの割合か?
ここまで計算できると、あとは単純な割り算です。
今回の検査での偶然じゃなく一致した部分の割合は0.222である一方、理論上はMax0.472の本当に一致したとみなされる割合の余地があります。
そのため、カッパ係数は以下の通り。
- カッパ係数:0.222/0.472=0.47
これら一連の考え方が、カッパ係数の算出方法です。
カッパ係数(k係数)をEZRで実施する方法

若干難しいカッパ係数の考え方をお伝えしましたが、EZRで計算すると簡単に実施することができます。
なので、EZRでやってみましょう。
EZRでカッパ係数の計算をしてみる
まずデータですが、用意しなくてOKです。
なぜなら、直接数値を入力するから。
ということなので、早速EZRの操作から解説します。
EZRの画面から、「統計解析」>「検査の正確度の評価」>「2つの訂正検査の一致度の評価(kappa係数)」を選択。
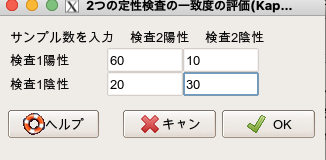
そして、先程の例に用いた検査Aと検査Bの数値を入力してみます。
そしてOKを押すと、下記にようにカッパ係数とその95%信頼区間が出力されます。

カッパ係数(k係数)の結果の見方:信頼区間は出るが検定はない

EZRでカッパ係数を求めるのはそれほど難しくなかったのではないでしょうか。
重要なのは結果の見方です。
カッパ係数が取り得る値は0〜1です。
というのも、「今回の結果の偶然じゃない一致度/理論上Maxの偶然じゃない一致度」という割合を示しているためですね。
じゃあ、どのぐらいの値だと一致度が良いとされる?かというと、さまざまな書籍やサイトを拝見すると以下のような基準が示されていました。
- 0.8を超える:高い一致度
- 0.6〜0.8:かなりの一致度
- 0.4〜0.6:中等度の一致度
- 0.4以下:低い一致度
ただし、あくまでも目安として捉えていただいてOKです。
そして、EZRの結果を見ていただければわかると思いますが、カッパ係数では95%信頼区間は算出されますが、統計的な検定はないです。
まとめ

いかがでしたか?
この記事では「カッパ係数(k係数)とは?EZRでの一致度の求め方と解釈の注意点」としてお伝えしました。
- カッパ係数ってそもそもどんな指標でどんな時に使えるの?
- カッパ係数をEZRで求める方法は?
- カッパ係数の結果の見方に注意点ある?
といったことが理解できるようになったのなら幸いです!
こちらの内容は動画でもお伝えしておりますので、あわせてご確認くださいませ。













コメント