回帰分析での目的変数と説明変数の違いをわかりやすく解説！独立変数と従属変数はどっち？

この記事では「説明変数」と「目的変数」について詳しく説明していきます。

回帰分析を学んでいると必ず出てくる「説明変数」と「目的変数」という統計用語。

そして違う教科書には「独立変数」とか「従属変数」という用語で出てきたりしていて、もうどっちがどっちか混乱してしまう。。。

という方もいるのではないでしょうか？

• 目的変数と説明変数の違い
• 独立変数と従属変数はどっちが目的変数で説明変数？
• 目的変数と説明変数はどう選ぶ？

といったことに関してお伝えしていきますね！

目的変数と説明変数の違いは？わかりやすく解説！

まずは目的変数と説明変数の違いから。

目的変数と説明変数を端的に説明すると、以下のような感じ。

• 説明変数：ある現象や値を説明する変数（何かの原因となっている変数）
• 目的変数：その説明変数（原因）を受けて発生した結果を表す変数

目的変数と説明変数を例でわかりやすく学ぶ

例えば、テストの点数と勉強時間を例に考えてみましょう。

「勉強時間を長く確保した方がテストで良い点が取れる」と考えたとすると、

テストの点数 = 定数 x 勉強時間 + 切片

という式でテストの点数を表すことができます。

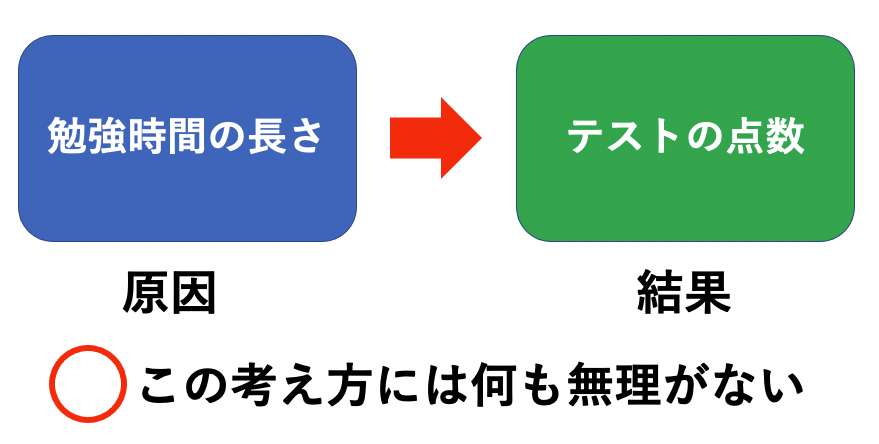
この例では、テストの点数は目的変数、勉強時間が説明変数となりますね。

勉強時間の長さはテストの点数に対する原因であり、テストの点数は勉強の長さを受けて出た結果である、と考えられるからです。

これは自然な考え方ですよね。

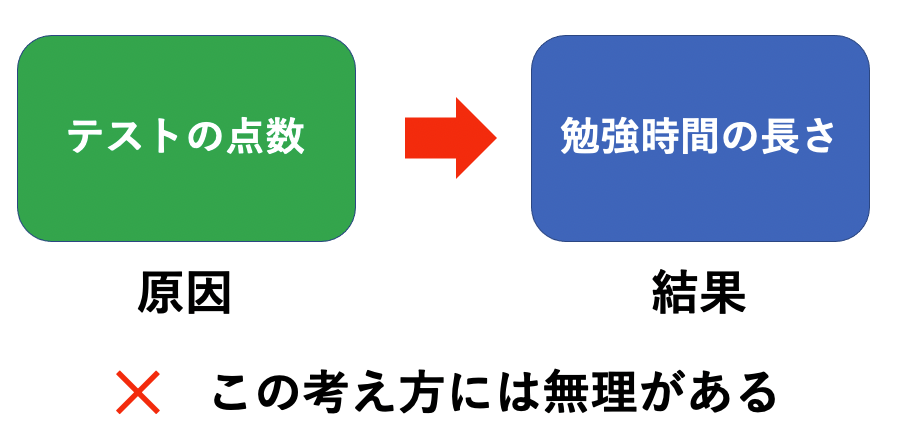
では逆に、勉強時間が目的変数であり、テストの点数が説明変数と考えた場合はどうなるでしょうか？

普通、勉強というのはテストの前に実施するものなので、テストの点数は勉強時間の長さに対する原因であり、勉強の長さはテストの点数を受けて出た結果である、と考えるのはかなり無理があります。

なので、目的変数と説明変数は「原因と結果」という違いをちゃんと反映したものになっているのか、ということを強烈に意識しなきゃいけないんです。

この「原因と結果」という関係は、どんな回帰分析でも同じ考え方です。

共分散分析であろうが、ロジスティック回帰分析であろうが、Cox比例ハザードモデルであろうが、同じ考え方をしましょう！

独立変数と従属変数ってどっちが目的変数でどっちが説明変数？

独立変数と従属変数という言葉も、統計の教科書ではよく出てきますね。

説明変数と目的変数は何が違うのでしょうか？

答えは、どちらも同じものを指します。

呼び方が違うだけですね。

説明変数の違う呼び方と英語表記

説明変数に関しては、他にも下記のような呼び方があります。

どんな呼び方にしろ同じことを言っていますので、「原因」を示した変数なんだなということでイメージしてください。

• 説明変数：explanatory variable
• 予測変数：predictor variable
• 独立変数：independent variable

目的変数の違う呼び方と英語表記

目的変数に関しても、他にも下記のような呼び方があります。

どんな呼び方にしろ同じことを言っていますので、「結果」を示した変数なんだなということでイメージしてください。

• 目的変数：response variable
• 結果変数：outcome variable
• 従属変数：dependent variable
• 応答変数：response variable

目的変数と説明変数はどう選ぶ？

目的変数と説明変数の違いが分かったところで、実践編ですね。

実際の臨床研究で目的変数と説明変数をどう選ぶか？ということです。

（そんなの簡単だよ、原因と結果を考えればいいんでしょ。）

と思うかもしれないですが、実は結構多くの方が混乱していたりするので、ここでちゃんとおさらいしておきましょう。

目的変数と説明変数を選ぶにはデータ取得の時系列を考えることが大切

臨床研究は大きく分けて「前向き研究」「後ろ向き研究」「横断研究」がありますよね。

この研究の種類によってエビデンスレベルが変わるというのは多くの方が知っていることでしょう。

じゃあなぜエビデンスレベルが変わるのかというと、いちばんの大きな理由は「データの取得方法が違う」からなんです。

前向き研究であれば、取得したいデータをこれから取得すれば問題ありません。

しかし後ろ向き研究になると、解析したいデータがあっても過去に取得していないデータであれば取得不可能ですし、例えば「あの時を思い出して点数をつけてください」と記憶を遡ってもらうとしても、正確ではありません。

例えば、以下のような研究目的があったとします。（架空の目的です）

つまり、「コレステロール」が原因（説明変数）で、「がんのなりやすさ」が結果（目的変数）、ということですよね。

そこでデータの取り方として、現時点で「がん患者」と「がんじゃない人」の現時点の「コレステロール」を取得したとしましょう。

そして結果として、「がん患者」と「がんじゃない人」でコレステロールの平均値に違いがありました。

この時に結論として「コレステロールの違いによって、がんになりやすさが違う」という結論が導き出せるでしょうか？

答えは「No」です。

なぜなら、現時点で「がん患者」と「がんじゃない人」の現時点の「コレステロール」を取得してしまうと、「コレステロール値の違いによってがんになりやすさが違う」のか「がんになった結果としてコレステロール値に違いが出た」のか、という原因と結果の切り分けができないからです。

つまり上記のようなデータの取得方法をしてしまうと、コレステロールの値が原因なのか、がんの発生が原因なのか、どっちがどっちなのか分からないんです。

だからこそ、説明変数と目的変数を選ぶ際には「データの取得方法（特にデータ取得の時系列）」がとても大事になります。

原因（説明変数）と結果（目的変数）が明確に決められない場合には、関連を確認する、ということまでしかできません。

関連を確認するというのは、いわゆる「相関係数を算出する」ということですね。

逆を言えば、相関係数を算出して相関関係を確認したとしても、どっちが原因でどっちが結果なのか、ということまでは相関からは分からない、ということです。

ぜひこの点は意識してくださいね！

Rで目的変数と説明変数を深く理解する

実際に、サンプルデータを用いて説明変数と目的変数の違いを深く理解していきます。

datariumというパッケージに含まれるmarketingというサンプルデータを使います。

サンプルデータを用いて、下記の解析を実施します。

• sales（売り上げ）を目的変数として、youtube（youtubeの広告費）を説明変数とした回帰分析
• youtube（youtubeの広告費）を目的変数として、sales（売り上げ）を説明変数とした回帰分析

まずは一つ目のsales（売り上げ）を目的変数として、youtube（youtubeの広告費）を説明変数とした回帰分析を実施します。下記のプログラムを実施します。

#1度だけ実施する。過去にインストールしたことがあれば実行しなくてOK
install.packages("datarium")
install.packages("dplyr")

# パッケージの読み込み
library(dplyr)

# データの読み込み
data("marketing", package = "datarium")

# データの確認
head(marketing, 3)

# sales（売り上げ）を目的変数、youtube（youtubeの広告費）を説明変数とした回帰分析
fit <- lm(sales ~ youtube, data = marketing)

#解析結果の確認
summary(fit)

上記のプログラムを実施し、回帰係数の結果だけを取り出してくると下記のようになりました。

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 8.439112   0.549412   15.36   <2e-16 ***
youtube     0.047537   0.002691   17.67   <2e-16 ***

結果として確認したいのはyoutubeの行で、Estimate（回帰係数の推定値）が0.0475、そのp値は2*10^-16未満という、かなり小さいp値であることがわかります。

つまり、youtubeの広告費は売り上げに影響がありそうだ、という結論になります。

では次に、youtube（youtubeの広告費）を目的変数として、sales（売り上げ）を説明変数とした回帰分析を実施してみます。

# youtube（youtubeの広告費を目的変数、）sales（売り上げ）を説明変数とした回帰分析
fit2 <- lm(youtube ~ sales, data = marketing)

#解析結果の確認
summary(fit2)

上記のプログラムを実施し、回帰係数の結果だけを取り出してくると下記のようになりました。

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) -40.1403    13.0763   -3.07  0.00244 ** 
sales        12.8717     0.7285   17.67  < 2e-16 ***

結果として確認したいのはsalesの行で、Estimate（回帰係数の推定値）が12.87、そのp値は2*10^-16未満という、かなり小さいp値であることがわかります。

つまり、売り上げはyoutubeの広告費に影響がありそうだ、という結論になります。

しかしここで考えていただきたいのが、「売り上げはyoutubeの広告費に影響がありそうだ」という結論は、「原因と結果」を考えたときに適切でしょうか？

もしかしたら適切な解釈になる可能性は0ではありませんが、通常は「広告費が原因で、売上は結果である」と考える方が自然です。

そのため、後者の解析は不適切な可能性がある、ということ。

回帰分析では上記の通り、原因（説明変数）と結果（目的変数）が逆でも解析結果が出てしまいます。

そのため、解析をする前に何が原因（説明変数）であり、何が結果（目的変数）なのかを十分に考えて解析を実施する必要があります。

まとめ

最後におさらいをしましょう。

ぜひ違いを意識して、適切に使っていきましょう！！