ROC曲線とは？わかりやすくカットオフ値の決め方やAUCの意味まで解説！

ROC曲線は、分類モデルの性能を評価するための方法の一つです。

医療統計の中では「検査の陽性/陰性」と「疾患の有無」といった、検査の性能を評価する際によく用いられる方法。

コロナウイルスが流行した際に、PCR検査でも話題になりました。

PCR検査を行なうと下の表のように偽陰性や偽陽性が出る、というのは耳にされた方が多いのではないでしょうか。

	疾患あり	疾患なし
検査 : 陽性	真陽性	偽陽性
検査 : 陰性	偽陰性	真陰性

これから解説するROC曲線というものを使うと、検査の有効性を分析することができるのでしっかり覚えておきましょう。

本記事では、ROC曲線とは何か、そしてその読み解き方について、初心者でも理解できるようにわかりやすく解説します。

分類モデルの評価においてROC曲線がなぜ重要なのか、その基礎知識から応用例、さらにはROC曲線の限界と注意点についても触れていきます。

 

ROC曲線とはわかりやすくいうとどんな曲線？感度と特異度を考慮した曲線

まず用語の定義から始めます。

• 真陽性：実際に疾患がある人が陽性と判断されること
• 偽陽性：実際には疾患がない人が陽性と判断されること
• 偽陰性：実際に疾患がある人が陰性と判断されること
• 真陰性：実際には疾患がない人が陰性と判断されること

	疾患あり	疾患なし
検査 : 陽性	真陽性（A）	偽陽性（B）
検査 : 陰性	偽陰性（C）	真陰性（D）

上の表の記号を使って真陽性率を算式であらわすと、真陽性率＝A/（A＋C）となり、これを感度と呼びます。

また、真陰性率＝D/（B＋D）となりこれを特異度と呼びます。

このとき、１－特異度＝B/（B＋D）となり、これを偽陽性率と呼びます。

 

つまり真陽性率（True Positive Rate：TPR）は、実際に疾患ありに属する人数のうち、正しく疾患ありと予測された人数の割合のことです。

偽陽性率(False Positive Rate：FPR) は、実際には疾患なしに属する人数のうち、誤って疾患ありと予測されたサンプルの割合のことです。

1から特異性を引いた値に等しく、検査が疾患なしをどれだけ誤って疾患ありと判断するかを示します。

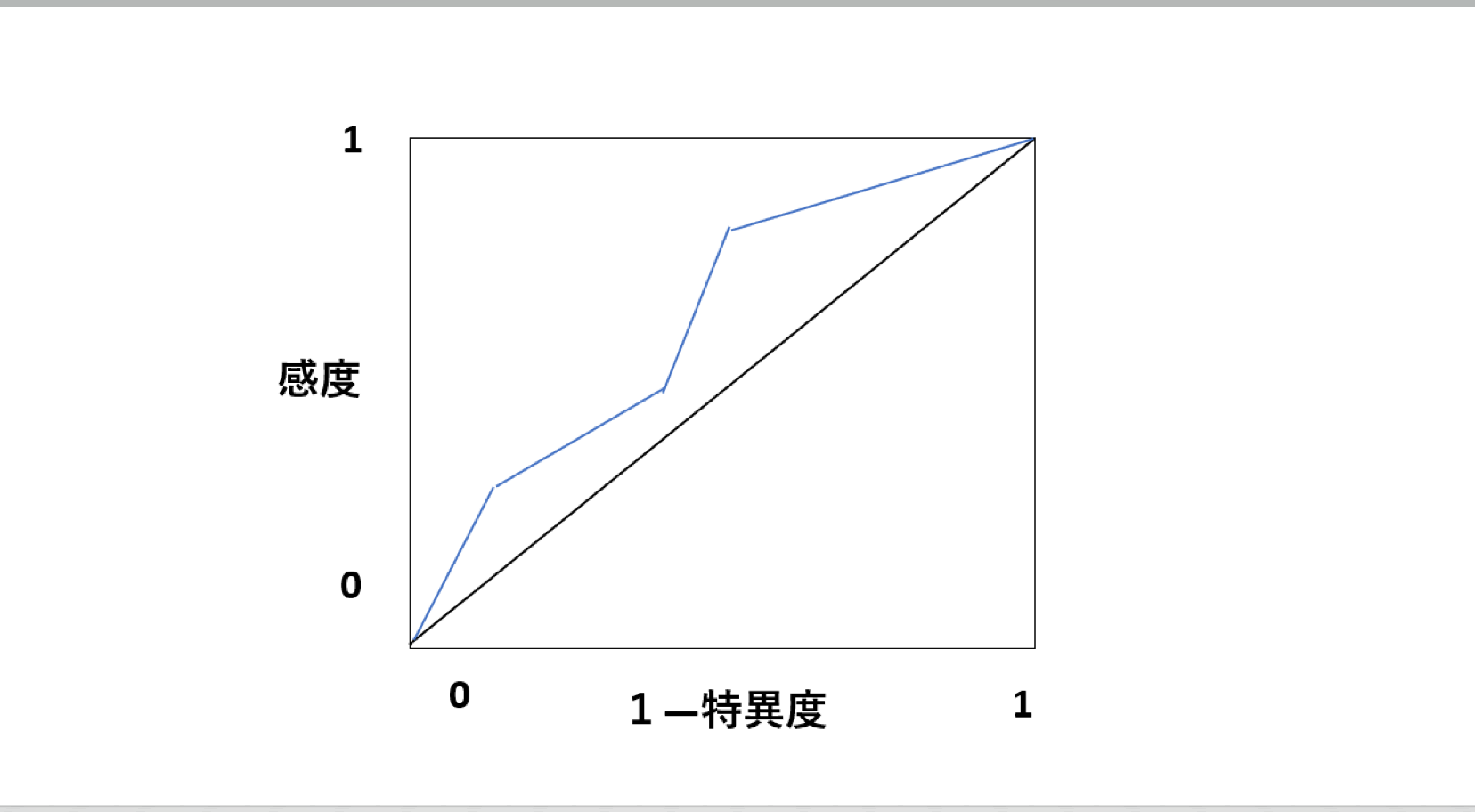
上のグラフのように横軸（0から1まで）に１－特異度、縦軸（0から1まで）に感度をプロットし、カットオフ値（検査の基準値）を連続的に変化させた際に描かれる曲線（上のグラフでは青い色の線）のことをROC曲線と呼びます。

 

PCR検査でROC曲線を考える：具体的な書き方は？

カットオフ値を下げれば下げるほど感度 (＝陽性率) は高くなる、という性質があります。

PCR検査の例でいえば「唾液中のウイルス遺伝子量20フェムトグラム/デシリットル以上」がであれば検査陽性になりますが、、1フェムトグラムとは1グラムの1000兆分の1のことなのでほとんどないに等しいということを意味します。

ほとんどの人がこの基準を満たしますから、感度は限りなく1に近づきます。

その一方で、特異度は極めて小さく、0に近いはず。

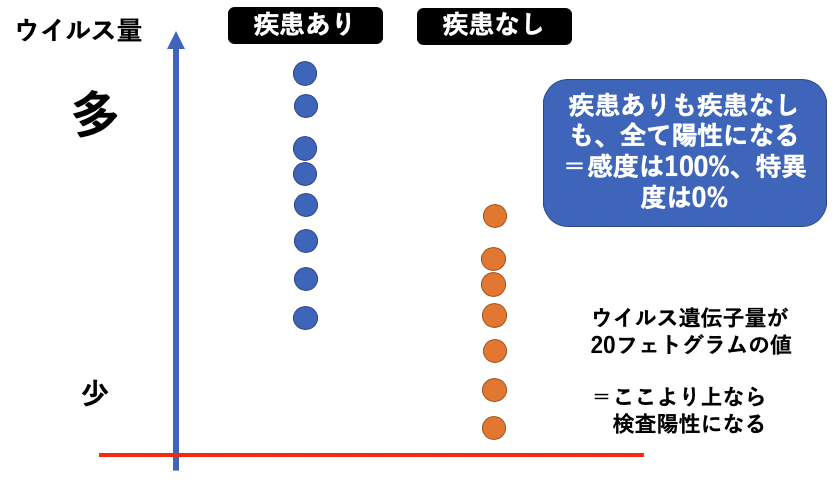
すなわち、１－特異度は1に近い数値になります。したがって、このカットオフ値はROC曲線でいえば右上の部分にプロットされます。

ではここから、カットオフ値を徐々に上に上げていきましょう。

 

例えば以下のような図だと、疾患ありの8人の中で、陽性になる人は7人ですから、感度は7/8=87.5%になります。

一方で疾患なしの7人のうち、4人が検査陰性になるので、特異度は4/7=57%になります。

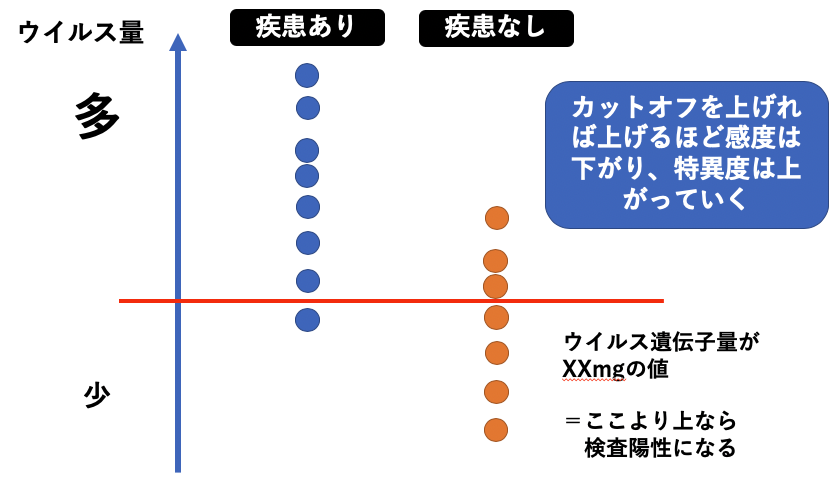
つまり、カットオフ値を上げれば上げるほど感度 (＝陽性率) は低くなるのですが、特異度は上がっていく。

そしてカットオフ値を1番上まで持っていくと、感度は0になり、特異度は100%になります。

これは「感度と特異度はトレードオフの関係がある」ということです。

 

このようにして、カットオフ値を変化させていけば、左下から徐々に右上に向かう、以下のような形状の曲線になるのです。

ROC曲線は、このように一辺の⻑さが１の正⽅形の中に定義される曲線です。

ROC曲線は、でたらめな検査であれば45度の直線になり、有効な検査であれば45度の線から左上に離れた曲線になります。

ROC曲線が45度の線から左上に離れれば離れるほど検査は有効性が高いということになるのです。

ROC曲線から計算するAUCの意味は？

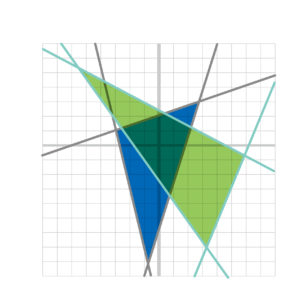
次にAUC（Area Under the Curve）という概念について説明します。

AUCとは、ROC曲線の下側の⾯積のこと。

ROC曲線とは偽陽性率と真陽性率が基準値に対してどのように変化するかを示す曲線なので、ROC曲線を用いて算出されるAUCはある検査がどれくらい有用性があるのかの指標となるのです。

 

なぜROC曲線を用いて算出されるAUCが検査の有用性の指標となるのか？

AUCはROC 曲線の下の面積ですので、ROC 曲線の性質から、でたらめな検査のときにAUCが0.50になり、完璧な検査のときにAUCは1になることが理解できるかと。

このように、疾患ありと疾患なしを識別できる程度が ROC 曲線下の面積に反映されるため、AUCにより検査の総合的な評価を行うことが可能となります。

AUCは、検査の総合的な性能を１つのスコアにカットオフ値によらない形で実現した指標と言えるでしょう。

ROC曲線からカットオフ値の決め方は？

では、ROC曲線からカットオフ値を決めるにはどうしたらいいか。

ROC曲線からカットオフ値を決める方法はいくつかありますが、ここでは①グラフの左上、座標でいうと（0,1）からの距離を最小にする方法と、②Youden’s indexというものを用いた方法の２とおりの方法をご紹介します。

ROC曲線からカットオフ値の決め方1：左上の隅の点からの距離が最小となる方法

この方法は、後述するYouden’s indexと違ってスマートな名前がありません。

とりあえず、「左上の隅の点からの距離が最小となる方法」としておきます。

感度と１－特異度という２つの変数からなるROC曲線は、これまで説明したとおり、45度の線から左上に離れれば離れるほど検査としての有効性が上がることが理解できるのでは。

したがって、左上の隅（0,1）との距離が最小となる点をカットオフ値にするという方法が、まず一つの方法としてあり得るのです。

これはスマートな名前がなくて覚えにくいですが、内容は結構シンプルですよね。

ROC曲線からカットオフ値の決め方2：②Youden’s index

次にYouden’s indexというものについて説明します。

これは感度も特異度も高いほうがいいと考えて、（感度+特異度）が最大になる点を最適点と定義する方法です。

具体的には、最も検査の有効性が低いROC曲線、すなわちAUC = 0.5となる45度の線から最も離れたポイントをカットオフ値にすればいいということ。

45度の線から縦軸方向の距離を計算すると（感度+特異度－1)となりますが、これが最大値となるポイントをカットオフ値にしてしまえばいい。

これは、①の方法の逆の考え方になっています。この(感度+特異度－1)が最大値となる点をYouden indexと言います。

これはちゃんと名前が付いていて覚えやすい。

まとめ

ROC曲線は、検査や診断薬の性能最適な境界値を推定する方法のひとつです。

ROC曲線は感度と特異度しか考慮しませんが、複数の検査項目のROC曲線をひとつのグラフ上に描くことができるため、複数の検査項目について診断指標としての性能を比較することができます。

ROC曲線は、検査や診断薬の性能最適な境界値を推定する方法のひとつですが、実は万能な方法ではありません。

そんな神のような完璧な方法があるわけないですよね。

ですが、直観的に理解しやすく扱いやすい手法と言えます。

どんな方法にも短所と長所がありますので、それぞれの研究目的に合った方法を選択する必要があるのです。

ROC曲線を用いた分析手法を皮切りにさまざまな分析手法を勉強していきましょう。

 

＞＞JMPでROC曲線を作成する方法！

＞＞EZRでROC曲線とAUCを算出する方法