カイ二乗検定には、イェーツの連続補正をかける方法と補正をかけない方法があります。
「イェーツの連続補正って何のこと？」
「補正は必要なの？」
といった疑問をお持ちの方も多いのではないでしょうか。
本記事では、イェーツの連続補正とは何か？どんな時に必要なのか？といった疑問にお答えします。
なるべく分かりやすく説明していきますので、初心者の方も安心してくださいね！
Contents
カイ二乗検定におけるイェーツの連続性補正とは？
カイ二乗検定におけるイェーツの連続補正をまずは理解していきましょう！
カイ二乗検定とは？
イェーツの連続補正の話をする前に、カイ二乗検定について説明しておきます。（すでに知っている方は飛ばしても構いません）
カイ二乗検定とは、ある群とある群の比率の差に違いがあるかどうかを検証する手法の一つです。
具体的には実測値のクロス集計表を作成した後、実測値と期待値(2群の差がない時に当てはまる理論値)とのズレがどれくらい大きいか算出します。
この実測値と期待値のズレをカイ二乗値と呼び、カイ二乗値が大きければ大きいほどp値が小さくなっていきます。
カイ二乗検定について詳しく知りたい方はこちらの記事をご覧ください。
カイ二乗検定の問題点
非常に便利なカイ二乗検定ですが、統計家のフランク・イェーツがある問題点を指摘しました。
それは”カイ二乗検定は実際より甘い結果が出るんじゃないか？”という指摘です。
どういうことでしょうか？
カイ二乗検定は、クロス集計表から算出したカイ二乗値がカイ二乗分布に従っていることを前提として設計された検定法です。
しかしイェーツ氏によれば、カイ二乗値とカイ二乗分布に小さなズレがあり、そのズレの影響で本来より有意差が出やすい結果になってしまうのではないかというわけです。
有意差が出やすいということは、本来有意差がないのに有意差があるという間違った結果が出るリスク(第一種の過誤、αエラー)が高くなるということです。
このような間違いはあってはならないものですので、イェーツ氏の指摘が本当なら何らかの対策が必要ですよね。
そこで生み出されたのが、イェーツの連続補正です。
イェーツの連続補正とは？
イェーツの連続補正とは、カイ二乗検定の時に算出するカイ二乗値に補正をかけて有意差が出やすくならないように調整することです。
これによって本来有意差がないのに有意差があるという間違った結果になるリスクを下げられるというわけです。
ただしイェーツの補正をかけると必要以上に厳しくなってしまうこともあるので注意が必要です。
何でもかんでも補正をかければいいということではありません。(どんなときに補正をかけるべきかは後述します)
カイ二乗検定でイェーツの連続補正をした場合にはどんな違いがある？
ではカイ二乗検定で、イェーツの連続補正をした場合としていない場合ではどんな違いがあるのでしょうか？？
イェーツの連続補正の導出
イェーツの連続補正とは、カイ二乗値に補正をかけてp値が小さくなりすぎないように（有意になりやすくなることを防ぐように）調整する方法でした。
実際にどんな補正をかけているのか確かめてみましょう。
こちらは通常(連続補正なし)のカイ二乗値の算出方法です。
こちらはイェーツの連続補正をかけてカイ二乗値の算出方法です。
ご覧のように、イェーツの補正は0.5を引くことでカイ二乗値が少し小さくなるように補正しています。
結構単純ですよね。
カイ二乗値が小さくなるとp値が大きくなりますので、有意差が出にくくなるというわけですね。
イェーツの連続補正をかけた時とかけない時の結果の差
実際にイェーツ補正をかけた時とかけない時でどれくらい結果が変わるのかみていきましょう。
今回は例としてこのようなデータを使ってみます。
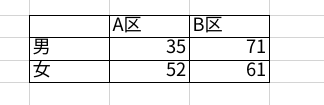
A区とB区で男女比に差があるかどうか調べたいとしましょう。
さっそくカイ二乗検定をかけてp値を算出してみましょう。
- イェーツ補正なし：p=0.049
- イェーツ補正あり：p=0.068
イェーツ補正をかけるとp値が高くなることが分かりますね。
差はわずかですが、有意水準をp<0.05とした場合、イェーツ補正の有無によって反対の結果になることが分かります。
このようにイェーツ補正をかけるか否かは事前にしっかり検討しておかなければなりません。
ではどんな時にイェーツ補正をかけた方がよいのでしょうか？
解説していきますね。
イェーツの連続補正はどんなときに必要？
では、イェーツの連続補正が必要な時とはどんなときでしょうか？
イェーツの連続補正が必要な場合1：厳しく検定を実施したいとき
有意差があるかどうか、厳しく判断したい時はイェーツの連続補正をかけるようにしましょう。
今までご説明したとおり、イェーツ補正をかけるとp値が少し大きくなるからです。
間違った有意差（αエラーを起こすこと）が絶対に出てはいけない場面ではイェーツ補正をかけましょう。
たとえば新しい薬の効果を検証するときなどですね。(効果のない薬を間違っても効果があると言ってはいけませんよね)
反対に有意差があるものを少しでも見逃したくない場面では補正をかける必要はないでしょう。
ビジネスの現場である施策が有効かどうかとりあえず検証したいときなどです。
このようにどのような目的でカイ二乗検定を使うかによって、補正をかけるべきかどうかは変わってきます。
ひとまずイェーツ補正をかけるとp値が高くなるということだけは踏まえておきましょう。
どちらにすべきか迷ったら、ひとまず補正をかけることをおすすめします。
厳しく検定をして悪いことはないからです。
イェーツの連続補正が必要な場合2：期待値のクロス集計表の中に5より小さい値が含まれるとき
下図のようにクロス集計表に偏りがみられることがあります。
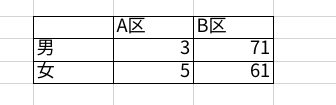
このような偏りがある場合(期待値のクロス集計表に5以下の値が含まれる場合)はイェーツ補正をかけたほうが良いと言われています。
集計表に偏りがあると、カイ二乗値とカイ二乗分布のズレが大きくなるからです。
実測値ではなく期待値が5以下の時であることに注意してください。
実質このような場合にはカイ二乗検定をすること自体やめたほうがよく、フィッシャーの正確確率検定を使うほうがいいですね！
イェーツの連続補正が必要な場合3：データ数が非常に少ないとき
先ほどと同様の理由で、全体のデータ数が非常に少ない時もイェーツの連続補正をかけたほうが良いと言われています。
データ数が少ないと必然的に期待値が5以下になるからです。
期待値のクロス集計表に5以下のマスがなくなるくらいデータ数が多くなければ補正をかけるようにしましょう。
実質このような場合も同様に、カイ二乗検定をすること自体やめたほうがよく、フィッシャーの正確確率検定を使うほうがいいですね！
まとめ
最後におさらいをしましょう。
- イェーツの連続補正とは、p値が少し高くなるよう補正すること
- イエーツ補正をかけると間違った有意差が出にくいメリットがある
- イェーツ補正をかけると検出力が下がるデメリットがある
- 厳しく検定をかけたい時や、データ数が少ない時、データに偏りがある時はイェーツ補正をかけたほうが良い
カイ二乗検定を知っている方は多いですが、イェーツ補正について知っている方は少ない印象があります。
若干の差ではありますが、補正の有無で結果に差が出るためカイ二乗検定をかける時はイェーツ補正についても考慮するようにしましょう！
最後までお読み頂きありがとうございました。
動画でも解説しておりますので、ぜひ記事とセットでご確認くださいませ^^
第1章：臨床研究ではなぜ統計が必要なのか？計画することの重要性
第2章：研究目的をどれだけ明確にできるのかが重要
第3章：p値で結果が左右される時代は終わりました
第4章：多くの人が統計を苦手にする理由
第5章：統計を使えるようになるために今日から何をすれば良いか？
第6章：統計を学ぶために重要な環境
もしあなたがこれまでに、何とか統計をマスターしようと散々苦労し、何冊もの統計の本を読み、セミナーに参加してみたのに、それでも統計が苦手なら…
私からプレゼントする内容は、あなたがずっと待ちわびていたものです。
