フィッシャーの正確確率検定とは？カイ二乗検定との違いをわかりやすく

分割表で出てくる検定は2つです。

それは、「カイ二乗検定」と「フィッシャーの正確確率検定」。

 

フィッシャーの正確確率検定は、フィッシャーの直接確率検定とも呼ばれますね。

でも、分割表の検定としてはフィッシャー正確確率検定の他にもカイ二乗検定があります。

ではカイ二乗検定とは何が違うの？という疑問も出てきますよね。

 

そのためこの記事では、フィッシャーの正確確率検定の概要、そしてカイ二乗検定との違い、最後に計算式について解説していきます！

 

フィッシャーの正確確率検定でやっていることは、カイ二乗検定と一緒

フィッシャーの正確確率検定。

T検定とかF検定とかと比べると、やたら長い名前です。

その仰々しい名前から、「なんか難しそう・・・」とあなたは思っているかもしれませんね。

でも、まったく難しくないです！！

なぜならフィッシャーの正確確率検定がやっていることは、カイ二乗検定と一緒ですから。

詳しくはカイ二乗検定のページで見てほしいんですが、念のため少しだけ復習します。

カイ二乗検定もフィッシャーの正確確率検定も、以下のことをやっています。

 

 

フィッシャーの正確確率検定とカイ二乗検定ではどこが違うの？

具体的にフィッシャーの正確確率検定と、カイ二乗検定の違いが知りたい！

と思いますよね。

当然です。

2つあるなら、どこか違う部分があるはず。

 

実はこの2つの検定、ある部分が違います。

 

 

ここが違う部分です。

 

カイ二乗検定は、T検定と手順が同じイメージ

カイ二乗検定がどのように数値を出しているかというと、次の手順で算出しています。

 

 

つまり、T検定なんかと一緒です。

T検定は、T値と呼ばれる検定料を算出して、それをT分布表と見比べてP値を出します。

 

フィッシャーの正確確率検定は、分布表と見比べることをしない

一方、フィッシャーの正確確率検定はどうしているか。

その名の通り確率を「正確に」計算しています。

そして、ここで言う「確率」がP値のことです。

 

フィッシャーの正確確率検定とカイ二乗検定では多少P値が異なる

χ二乗検定は、P値を導き出すまでにχ二乗値を経由します。

そのため、近似した計算方法と言えます。

一方でフィッシャーの直接確率検定は、「直接」P値を算出します。

つまり、両者の方法で算出したP値は、多少違うのです。

 

例えば、あるデータでカイ二乗検定を実施すると、下記のようにP=0.03767でした。

これと同じデータでフィッシャーの正確確率検定を実施すると、P=0.03683になります。

 

フィッシャーの正確確率検定とカイ二乗検定でどっちの方法を取ればいいの？

２つの検定の違いがわかりました。

そうなると、使い分けが気になるところですね。

それは分割表基礎でお示ししたように、データ数が5以下のセルが一つでもある分割表では、フィッシャーの直接確率検定を推奨します。

 

例えば、以下のような分割表があった場合。

5以下のセルが一つもないため、χ二乗検定を使ってOKです。

 

一方で、以下のような分割表があった時。

女性の効果なし、のセルが３ですよね。

この場合には、フィッシャーの直接確率検定を使う必要があります。

 

なぜかというと、χ二乗検定は近似した方法のため、ある程度データ数が多い場合に、ちゃんとしたP値を出してくれるからです。

また、フィッシャーの直接確率検定は、膨大な確率計算をする必要があるため、計算力が必要になります。

現在のPCは高性能になりましたが、それでもデータ数が多い場合にはフィッシャーの直接確率検定は時間がかかります。

その使い分けの目安が、データ数が5以下のセルが１つでもあるかどうかです。

 

ただ、一つだけ勘違いしていただきたくないのは、「フィッシャーの正確確率検定は、データ数が大きい場合でも使える」ということ。

カイ二乗検定は「データ数が大きい時”だけ”使える検定」ですが、フィッシャーの正確確率検定は「データ数が小さくても大きくてもどちらでも使える」検定です。

 

フィッシャーの正確確率の計算方法を具体的にわかりやすく！

フィッシャーの正確確率検定とカイ二乗検定の違いがわかりました。

フィッシャーの正確確率では、P値を「正確に」計算しているのでしたよね。

では次に気になるのは、そのP値の計算方法。

ということなので、その計算方法を具体的な例を用いて解説します。

 

例えば、以下のような合計18人のデータからなる表があったとします。

 

	肉が好き	魚が好き	合計
女性	2	6	8
男性	5	5	10
合計	7	11	18

 

この表で、男性なのか女性なのかと肉が好きなのか魚が好きなのかという２つの指標が、独立なのかどうかを検定したいとしましょう。

 

フィッシャーの正確確率検定の帰無仮説と対立仮説を整理する

検定の場合には、帰無仮説と対立仮説が必ずありますね。

この表の場合の帰無仮説と対立仮説は、このようになります。（片側検定を想定しています。）

 

• 帰無仮説：「性別と肉魚の好みは独立である（性別によって好みは変わらない）」
• 対立仮説は「女性の方が魚が好きな傾向がある（性別によって好みに差がある）」

 

フィッシャーの正確確率検定の方針

まずは検定の方針を解説します。

例えば、以下の通りに「肉が好きな女性」のカテゴリの人数を仮にaと置きます。

すると、他の３つのカテゴリの人数もaと使って以下のように表すことができます。

 

	肉が好き	魚が好き	合計
女性	a	8-a	8
男性	7-a	3+a	10
合計	7	11	18

 

このときに、a=2が実際にどれぐらい珍しいことなのかを、確率を計算することによって評価します。

「a=2が珍しい」のであれば、計算結果の確率は小さくなるはずです。

 

フィッシャーの正確確率検定の計算式

帰無仮説は「性別と肉魚の好みは独立」ですから、「8人の女性と10人の男性、合わせて18人から、７人の肉好きがランダムに選ばれる」
という状況を想定します。

この時、３種類の計算をします。

 

1. 「女性が２人選ばれて男性が５人選ばれる」ような確率を計算
2. 「女性が１人選ばれて男性が６人選ばれる」ような確率を計算
3. 「女性が０人選ばれて男性が７人選ばれる」ような確率を計算

 

数式としては、以下の通りですね。

１の場合の数式（P1）

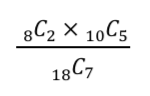
２の場合の数式（P２）

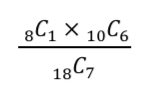
３の場合の数式（P３）

 

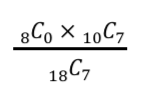
この３つの計算式から得られた３つの数字（確率）を全て足し合わせます。

つまり、P=P1+P2+P3を求めます。

ここで得られたPが、フィッシャーの正確確率検定のP値になります。

 

カイ二乗検定では、カイ二乗値を計算し、得られたカイ二乗値をカイ二乗分布表と見比べました。

そのため、P値を正確に計算するのではなく、近似したP値を得る方法、と言い換えることができます。

 

一方でフィッシャーの正確確率検定では、上記の計算の通りP値を「正確に」計算しています。

これが「フィッシャーの正確確率検定」と呼ばれる理由です。

 

フィッシャーの正確確率検定をEZRで実践する

フィッシャーの正確確率検定をEZRで実践する方法を、別記事で解説しています。

EZRとは無料の統計ソフトであるRを、SPSSやJMPなどのようにマウス操作だけで解析を行うことができるソフトです。

EZRもRと同様に完全に無料であるため、統計解析を実施する誰もが実践できるソフトになっています。

2019年5月の時点で英文論文での引用回数が2400回を超えているとのことで、論文投稿するための解析ソフトとしても申し分ありません。

これを機に、EZRで統計解析を実施してみてはいかがでしょうか？

 

＞＞EZRでフィッシャーの正確確率検定を実践する。

 

フィッシャーの正確確率検定に関してまとめ

• フィッシャーの直接確率検定も、根本的にχ二乗検定とやっていることは同じ。
• だが、P値を算出するための方法が違う。
• データ数が5以下のセルが一つでもある場合には、フィッシャーの直接確率検定が推奨される。

 

動画でもフィッシャーの正確確率検定に関してお伝えしていますので、ぜひご覧くださいませ！