この記事では「マクネマー（McNemar）検定とは？カイ二乗検定との違いや計算方法を解説」ということでお伝えします。
- マクネマー検定とは？カイ二乗検定との違い
- マクネマー検定を例題を用いて解説！
- マクネマー検定をEZRでやるとどうなる？
ということについて解説しますので、マクネマー検定について理解が進めば幸いです！
マクネマー検定（McNemar検定）とは？カイ二乗検定との違い
マクネマー検定は「対応のあるデータ」に対する2*2分割表の検定手法です。
2*2分割表に対する検定手法としてはカイ二乗検定やフィッシャーの正確確率検定があるけど、どう違うの？？と思われるかもしれません。
ですが、カイ二乗検定やフィッシャーの正確確率検定は「対応のない」分割表に対する解析手法。
つまり、データの対応の有無の違いが、マクネマー検定とカイ二乗検定・フィッシャーの正確確率検定の使い所の違いになります。
- 対応のあるデータの分割表：マクネマー検定
- 対応のないデータの分割表：カイ二乗検定 or フィッシャーの正確確率検定
マクネマー検定を例題を用いて解説！
では実際に、架空のデータでマクネマー検定を理解していきたいと思います。
今回は「ランニングを1ヶ月続けると肩こりが軽減するか？」という場合を想定。
100人のデータで、エクセルではこのようなデータです。
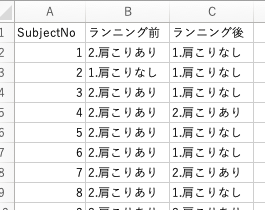
このデータに対して2*2分割表を作成すると、以下のようになります。
ランニング前と1ヶ月ランニングを続けた後のデータを、同じ人から取得している前提なので、対応のあるデータですね。
この時の帰無仮説と対立仮説は以下の通り。
- 帰無仮説：「ランニングが肩こりに影響なし」
- 対立仮説：「ランニングが肩こりに影響あり」
つまり、有意差が出たとすると「ランニングが肩こりに影響あり」という結論になります。
マクネマー検定の計算方法は？
マクネマー検定は、検定統計量c2を計算し、c2が自由度1のカイ二乗分布に従う、という前提で検定します。
では今回の例でc2を計算して自由度1のカイ二乗分布からP値を算出すると、以下の通りになります。
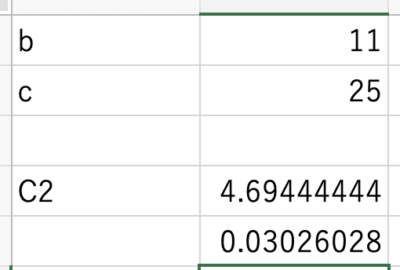
計算すると、統計量は4.694に、P値は0.03026になりました。
有意水準を0.05とすると有意差あり、ということですね。
手計算だとちょっと不安なので、EZRでも同じデータでマクネマー検定をしてみましょう。
マクネマー検定をEZRでやるとどうなる？
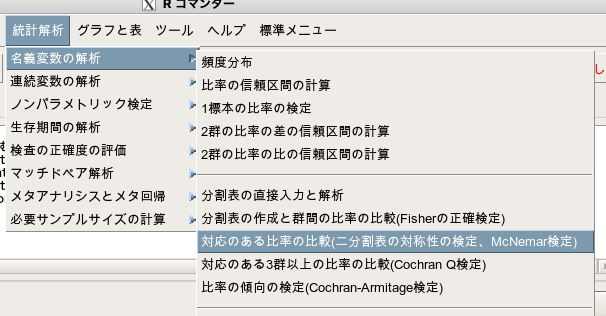
先程のデータを、EZRで計算してみます。
EZRでは「統計解析」＞「名義変数の解析」＞「対応のある比率の比較（二分割表の対象性の検定、McNemar検定）」で実施できます。
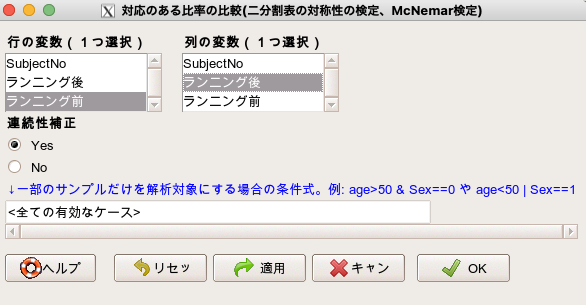
そして、行の変数に「ランニング前」を、列の変数に「ランニング後」を選択します。
そしてOKを押します。
すると結果が出力されます。
McNemar’s chi-squaredの検定統計量が4.96944であり、P値が0.03026となりました。
エクセルでの手計算と一緒の結果ですね。
まとめ
いかがでしたか？
この記事では「マクネマー（McNemar）検定とは？カイ二乗検定との違いや計算方法を解説」ということでお伝えしました。
- マクネマー検定とは？カイ二乗検定との違い
- マクネマー検定を例題を用いて解説！
- マクネマー検定をEZRでやるとどうなる？
ということについて理解が進んだのなら幸いです！
第1章：臨床研究ではなぜ統計が必要なのか？計画することの重要性
第2章：研究目的をどれだけ明確にできるのかが重要
第3章：p値で結果が左右される時代は終わりました
第4章：多くの人が統計を苦手にする理由
第5章：統計を使えるようになるために今日から何をすれば良いか？
第6章：統計を学ぶために重要な環境
もしあなたがこれまでに、何とか統計をマスターしようと散々苦労し、何冊もの統計の本を読み、セミナーに参加してみたのに、それでも統計が苦手なら…
私からプレゼントする内容は、あなたがずっと待ちわびていたものです。
