オッズ比とは？わかりやすく相対危険度（リスク比）との違いや計算法を簡単に解説！

この記事ではオッズ比とは？について、簡単にわかりやすく解説します。

オッズ比と相対危険度（相対リスク、リスク比）は、統計を学んでいくと必ずといっていいほど出てくる用語なので、恐らくあなたも一度は目にしたことがあるかもしれませんね。

ですが、オッズ比や相対危険度（相対リスク、リスク比）のことを、ちゃんと説明できるか？と言われたら、かなり難しいのではないでしょうか。

そのため、この記事では以下のことがちゃんと説明できるように、簡単にわかりやすく解説しました！

• オッズとリスクの定義
• オッズ比とリスク比の違い
• なぜ医療統計ではオッズがよく使われるのか

オッズ比とは？わかりやすく相対危険度（リスク比）との違いを意識しながら計算式の定義を確認しよう

　

まずは、オッズとリスクの定義を確認しましょう。

以下のような分割表があったとします。

　

	ガン発症	ガン未発症	合計
喫煙あり	A	B	A＋B
喫煙なし	C	D	C+D
合計	A+C	B+D	A+B+C+D

　

分割表に関しての詳しい解説は、別記事で解説していますので、そちらをご参照ください。

＞＞分割表に詳しくなる。

　

オッズ比の前にまずは相対危険度（以下、リスク比）の計算式の定義を確認する

この時、「喫煙あり」の集団で「ガンを発症」するリスクの定義は以下の通りです。

　

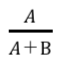
また、「喫煙なし」の集団で「ガンを発症」するリスクの定義は以下の通りです。

　

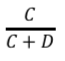
リスクって直感的にわかりやすいですよね。

日本語で説明すると、「喫煙をしていた集団の中でガンを発症した割合」「喫煙をしていない集団の中でガンを発症した割合」ですから。

そして、いわゆるリスク比（Relative Risk: RR）はこれらの比を取ったものです。

　

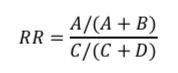
次に、オッズ比の計算式の定義を確認する

では、オッズの定義を確認しましょう。

オッズの正式な定義はp/(1-p)です。

pは、「喫煙をしていた集団の中でガンを発症した割合」であり、1-pは「喫煙をしていた集団の中でガンを発症していない割合」です。

ということは、p=A/(A+B)であり、1-p=B/(A+B)です。つまり、オッズとは、ある事象が起こる確率と起こらない確率の比ということ。

そのため、喫煙ありのオッズは次の通りになります。

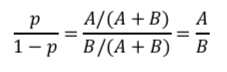
同様に、喫煙なしのオッズは次の通りとなります。

　

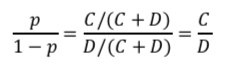
で、オッズ比（Odds Ratio: OR）はこれらの比です。

　

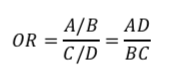
上記がオッズ比の定義です。

オッズ比とリスク比の違いは？簡単な練習問題で違いを理解

数式的には明らかに違うオッズ比とリスク比。

では、私たちはそれぞれの結果をどう解釈すればいいのでしょうか。

ここは重要なので、是非とも理解してください。

　

リスク比は〇〇倍という言い方ができる

例えば、先ほどの表に具体的な数字を入れてみましょう。

そして、一番右にリスクを足してみます。

　

	ガン発症	ガン未発症	合計	リスク
喫煙あり	3	2	5	60% (3/5)
喫煙なし	1	4	5	20% (1/5)
合計	4	6	10

　

このときのリスク比（Relative Risk: RR）は60%/20%=3となります。

RR=3となることから、以下の解釈ができます。

喫煙者がガンを発症するリスク（割合）は非喫煙者に比べて3倍である

リスク比が3=リスクが3倍になる、と解釈が可能です。

　

オッズ比は〇〇倍という言い方ができない

一方のオッズ。

また先ほどの表でオッズを出してみます。

　

	ガン発症	ガン未発症	合計	オッズ
喫煙あり	3	2	5	1.5 (3/2)
喫煙なし	1	4	5	0.25 (1/4)
合計	4	6	10

　

この時のオッズ比（Odds Ratio: OR）は1.5/0.25=6となります。

OR=6であるとき、以下のような解釈はできません。

　喫煙者は非喫煙者に比べて6倍ガンを発症しやすい　

この解釈は絶対にNGなので、ぜひ理解しておいてください。

　

では、オッズ比から何が読み取れるのでしょうか。

オッズ比は、複数のオッズ比があった時に、その値が大きいとか、小さいといったことがわかるだけなのです。つまり、あくまで関連の強さを示す指標として使用します。

だからオッズ比は、リスク比に比べ理解しにくく、そのため使い方に注意がとても必要なのです。

　

なぜ医療統計ではオッズ比がよく使われているの？

直感的にはリスクのほうが解釈しやすく、オッズはなんだか解釈がしにくいことがわかりました。

なので、常にリスクを使っておけばいいのでは？

と、あなたは思ったことでしょう。

でも、医療統計の世界では、オッズがよく使われているのです。

その理由は３つあります。

　

1. ロジスティック回帰分析との相性が良い
2. どんな研究にも使える
3. pが小さければ、オッズ比はリスク比の近似になっている

　

どういうことか、それぞれ詳しくみていきましょう。

　

オッズ比が使われる理由：オッズはロジスティック回帰分析との相性が良い

あなたはロジスティック回帰分析という手法を聞いたことがありますか？

医療業界のデータを扱ったことがあるなら聞いたことがあると思います。

ロジスティック回帰分析とは、以下の数式で与えられる回帰分析です。

　

　

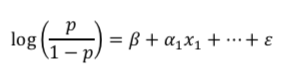
この部分、どこかでみませんでしたか？

　

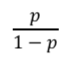
そう。

この部分は、オッズですよね。

つまり、ロジスティック回帰分析で私たちが求めているのは、オッズってことです。

医療統計ではロジスティック回帰分析を多用するため、結果的にオッズが多用されるのです。

　

ちなみに、リスク比を計算したい場合に用いる回帰分析は、ポアソン回帰か負の二項回帰です。

　

オッズ比が使われる理由：オッズはコホート研究でもケースコントロール研究でもどんな研究にも使える

臨床研究で有名な研究方法が２つあります。

それが「コホート研究」と「ケースコントロール研究」です。

ざっと簡単に「コホート研究」と「ケースコントロール研究」の違いを見てみましょう。

コホート研究は以下の通り。

 

この時、調査開始時点ではガンは発生しておらず、それから2年後（未来）にガンの発生を調べます。

このような研究をコホート研究といいます。

この研究は2年後の未来へ向かって調べる研究であり、「前向き」の研究といいます。

ケースコントロール研究は以下の通り。

すでにガンがあると診断された人、ガンではない人がいて、その時点から過去にさかのぼって喫煙をしていたかどうかを調べます。

このような研究をケースコントロール研究といいます。

この研究は過去へ向かって調べる研究であり、「後ろ向き」の研究といいます。

この研究方法の違いが何につながるのかというと、使える解析手法が異なるからです。

以下の表の通り、前向きに研究するコホート研究ではリスクもオッズも使えますが。

しかし、ケースコントロール研究ではリスクが使えないのです。

	リスク	オッズ
コホート研究	◯	◯
ケースコントロール研究	×	◯

なぜケースコントロール研究でリスクが使えないのか。

例を見てみましょう。

例えばケースコントロール研究をした結果、以下の表のデータがあったとします。（架空のデータです）

	ガン発症	ガン未発症	合計	リスク	オッズ
喫煙あり	150	50	200	0.75 (150/200)	3 (150/50)
喫煙なし	100	200	300	0.33 (100/300)	0.5 (100/200)
合計	250	250	500

この時、リスク比は0.75/0.33=2.25となります。

一方で、オッズ比は3/0.5=6となります。

では、ガン発症の人数が少なくなってしまって、100人しか集まらなかったとしましょう。

この時、以下のような表になったとします。

ガン発症の人は100人中60人（割合：60%）のため、250人中150人（割合：60%）の時と割合は同じですね。

	ガン発症	ガン未発症	合計	リスク	オッズ
喫煙あり	60	50	110	0.55 (60/110)	1.2 (60/50)
喫煙なし	40	200	240	0.17 (40/240)	0.2 (40/200)
合計	100	250	350

この時、リスク比は0.55/0.17=3.27となります。

一方で、オッズ比は1.2/0.2=6となります。

では、先ほどのガン発症の症例数が250人の場合と、今回のガン発症の症例数が100人の場合でのリスク比とオッズ比をまとめてみます。

ガン発症人数	リスク比	オッズ比
250人	2.25	6
100人	3.27	6

この表から見ても明らかなように、後ろ向き研究では選んでくるサンプル数が異なるとリスク比も違った結果になってしまう、ということです。

ガン発症人数を250人集めた時のリスク比は2.25倍だったのに対し、ガン発症人数を100人集めた時のリスク比は3.27倍になります。

このように、ケースコントロール研究の場合には、リスク比は症例数に依存してしまうため適切な解析手法ではありません。

その一方で、どんな症例数であっても、オッズ比は6です。

つまり、後ろ向き研究でのオッズ比は症例数に全く依存しません。

これが、ケースコントロール研究でオッズが使われるべき理由です。

オッズ比が使われる理由：確率pが小さければ、オッズ比はリスク比の近似になっている

３つめの理由は、割合が小さい場合に、オッズ比とリスク比は同じような値になるということです。

例を見てみましょう。

以下のようなデータがあったとします。

喫煙ありの割合（p）は0.03（＝30/1000）で、喫煙なしの割合（p）は0.01（＝10/1000）と、かなり小さいですよね。

	ガン発症	ガン未発症	合計	リスク	オッズ
喫煙あり	30	970	1000	0.03 (30/1000)	0.03 (30/970)
喫煙なし	10	990	1000	0.01 (10/1000)	0.01 (10/990)
合計	40	1960	2000

この時、リスク比は0.03/0.01=3であり、オッズ比も0.03/0.01=3です。

リスク比≒オッズ比であることがわかりますね。

臨床研究では、割合（p）が小さい研究をすることも多いです。

そのため、オッズ比の解釈がほぼリスク比の解釈として使うことが可能なので、有用です。

オッズ比とリスク比まとめ

• オッズとリスクは数式的に全く違う。
• リスク比は〇〇倍リスクが上昇する、という解釈ができるが、オッズ比はそのように解釈することができない。
• オッズ比は、以下の３つの理由があるため、臨床研究でよく使われる。
  1. ロジスティック回帰分析との相性が良い
  2. どんな研究にも使える
  3. 割合（p）が小さければ、オッズ比はリスク比の近似になっている

オッズ比とリスク比の違いに関して動画でも解説していますので、ぜひ併せてご覧くださいませ。

＞＞ロジスティック回帰分析とは？