カイ二乗検定は便利な検定で、ビジネスや研究などいろいろな場所で使われています。
基本的には2群間の割合の差を比較する時に使うカイ二乗検定ですが、
- 「3群以上の時はどうすればいいんだろう？」
- 「3群以上のカイ二乗検定をエクセルで計算する方法はあるの？」
と疑問に思う方も多いはずです。
本記事では、3群以上のカイ二乗検定をエクセルで行う方法や結果の解釈方法、解析時の注意点をご紹介します。
難しい計算式は使わずに、なるべく分かりやすく説明していきますね！
Contents
カイ二乗検定は3群以上の場合でもできる？
結論から言いますと、カイ二乗検定は3群以上の場合でもできます！
ただし2群で比較する時と比べて解釈の仕方が少し変わる点に注意が必要です！
どういった解釈をすればいいのかは、こちらの記事の後ろの方で解説しますね。
カイ二乗検定はエクセルでも出来ますので、今回はエクセルを使った計算方法をご紹介します。
ちなみにEZRというフリー統計ソフトを使うとエクセルよりも楽にカイ二乗検定が実行できます。
こちらの記事でEZRを使ってカイ二乗検定を実行する方法を紹介していますので、興味のある方はぜひご覧ください。
カイ二乗検定をエクセルで2×3分割表の計算の仕方
では、2×3分割表のカイ二乗検定をエクセルで実施する方法をお伝えしていきます！
2×3分割表のカイ二乗検定をエクセルで実施する全体の流れ
エクセルでカイ二乗検定を実行する手順は、以下のようになります。
- クロス集計表(2×3)を作る
- 別に期待値のクロス集計表(2×3)を作る
- CHISQ.TEST関数を使ってp値を算出
一つずつ順番に説明していきますね。
例として今回は「A区とB区とC区の住人に男女差があるかどうか、カイ二乗検定を行って確かめてみましょう」
クロス集計表(2×3)を作る
まずはクロス集計表を作りましょう。
「クロス集計表って何?」となる方もいると思いますので、クロス集計表を実際に作ってみますね。
A〜C区の住人の性別を集計したところ、以下のようになりました。
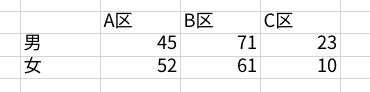
これがクロス集計表です。
一度は見たことがありますよね。
これでA〜C区の男女差が一目瞭然です。
次の手順で必要になるため、このクロス集計表に以下のように各列の合計値を追加しておきましょう。
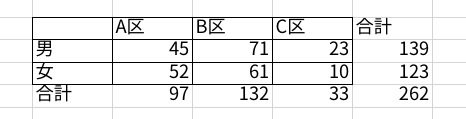
別に期待値のクロス集計表(2×3)を作る
次に期待値のクロス集計表を作ります。
ここで「期待値って何？」となりますよね。
カイ二乗検定の期待値とは、”各群に差がなかった場合に本来なるべき理論値”のことをいいます。
たとえば「A〜C区の男女比が同じ」と仮定すると、各区の男女比が全体の男女比と同じになるはずですよね。
ただ実際は理論通りぴったり同じになることはありませんから、あくまでも”期待値”という表現をしているわけです。
ひとまずは“期待値”=”群間差がない場合に本来なるべき値”と捉えておきましょう。
この期待値のおかげで、期待値から外れれば外れるほど群間に差があるという判断ができるというわけです。
前置きが長くなりましたが、実際に期待値のクロス集計表を作っていきましょう。
まずは先ほどのクロス集計表を複製し、中身の値だけ消しましょう。
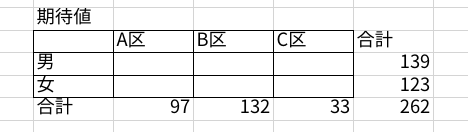
次に期待値をそれぞれ計算していきます。
期待値は”横列の合計”×”縦列の合計”÷”全体の合計”で計算できます。
A区の男性数の期待値は139×97÷262です。
全ての期待値を計算すると以下のようになります。
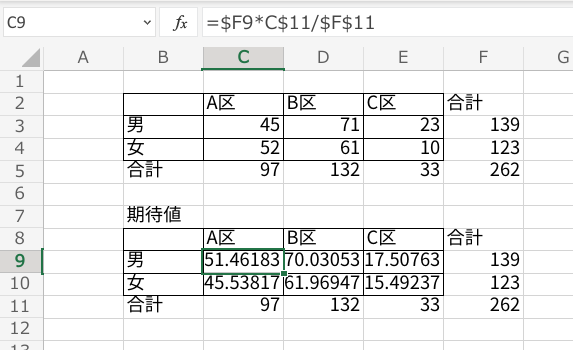
関数を使える方は上の図のように関数を作ると楽に計算ができますので、参考にしてください。
これで2つのクロス集計表ができました。
次はいよいよp値を算出してみましょう。
CHISQ.TEST関数を使ってp値を算出
p値の算出にはCHISQ.TEST関数を使用します。
下の図のように、好きなマスに”=CHISQ.TEST(実測値,期待値)”と入力しましょう。
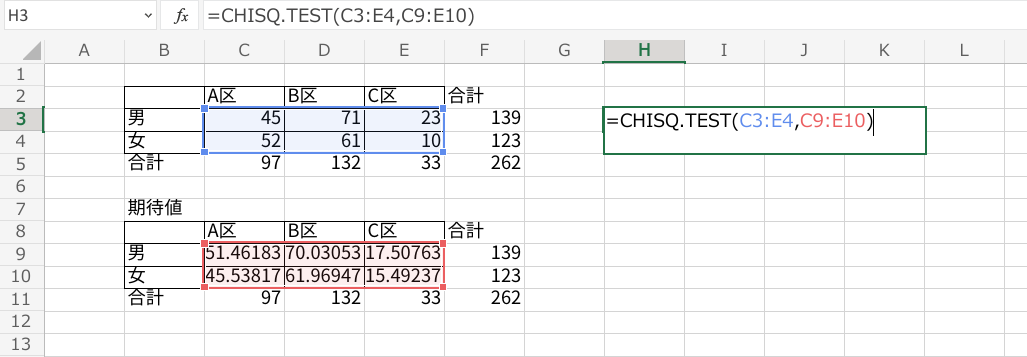
最後にEnterを押すとp値が算出されます。
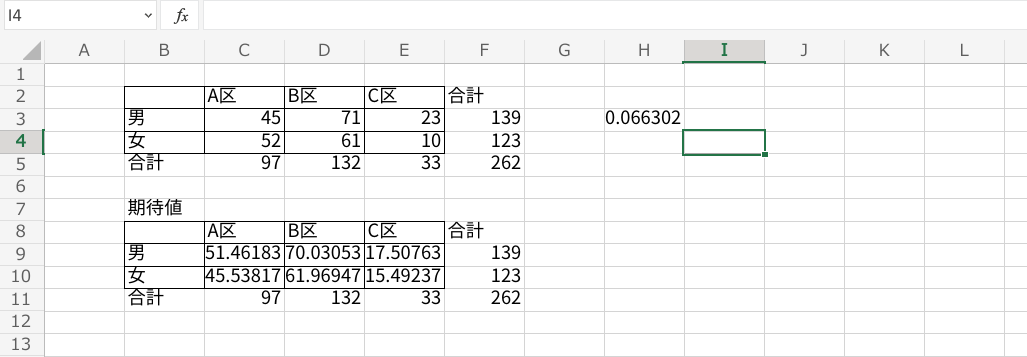
今回の例は0.05よりp値が大きいので、”各区の男女比に有意な差はない“という結論になります。
3群以上の比較にカイ二乗検定を行うと何がわかる？
3群以上でもカイ二乗検定を問題なく実施できることはわかりました。
重要なのは結果の解釈です。
3群以上のカイ二乗検定結果の解釈
3群以上の比較で有意差が出た場合、解釈に注意が必要です。
3群以上のカイ二乗検定では、比較した群の内どこか群間に差があることしか証明できないからです。
先ほどの例を使って説明していきましょう。
A区とB区、C区の男女比を比べるためにカイ二乗検定を利用し、有意差が出たとしましょう。
ただこの時A区とB区、B区とC区、C区とA区のどこに差があるのかまでは分かりません。
あくまでもどこかに有意差があるというのがわかるだけです。
では細かくどの群とどの群に差があるのか調べたい時はどうしたらいいでしょうか？
その場合は結局A区とB区、B区とC区、C区とA区で2×2のクロス集計表を作り、2群比較のカイ二乗検定を行う必要があります。
「なら最初から2群比較だけでいいんじゃないか？」
なんて声が聞こえてきそうですが、ビジネス等で使う分にはそれでも十分です。
ただし論文だと最初に全ての群で有意差が出ていることを編集者などから求められる場合があります。（私はそのような検定は不要だと思うのですが。。）
以上の理由から
「ひとまずどこかの群に差があるか確認したいだけ」
「論文で求められる可能性」
というケースでは3群以上のカイ二乗検定が役立ちます。
3群以上の比較をするときの注意点
先ほど細かく結果を見たいなら2群比較のカイ二乗検定が必要になることを説明しました。
さっそくカイ二乗検定をA区とB区、B区とC区、C区とA区の合計3回実行したいところですが、注意点があります。
簡単に説明すると、”繰り返し検定を実行する時はp値を厳しく設定しなければならない“という統計上のルールがあるということです。
ではどれくらい厳しく設定すればいいのでしょうか？
ここでは一番簡単なボンフェローニ法という手法を紹介します。
計算方法は簡単！有意水準を検定を実行した回数で割るだけです。
今回の例でいうと、0.05÷3=0.017が厳しく設定した有意水準になります。
3回検定した結果の内、どれかのp値が0.017を下回っていれば有意差ありと判断できます。
まとめ
最後におさらいをしましょう。
- カイ二乗検定で3群以上の比較は可能
- CHISQ.TEST関数を使うことでエクセルでp値の算出が可能
- 3群以上の比較ではどこか群間に差があることまでしか分からない
- 細かく知りたい場合は有意水準を厳しくした上で2群比較を繰り返し行う
「カイ二乗検定は2群比較にしか使えない」
なんて誤解をしている方をたまに見かけます。
しかしそんなことは全くなく、理論上は何群あっても利用することができます。
また今回は2×3のケースを紹介しましたが、3×3などのクロス集計表でもカイ二乗検定は実行できます。
必要に応じて使い分けて見てくださいね！
最後までお読み頂きありがとうございました。
第1章：臨床研究ではなぜ統計が必要なのか？計画することの重要性
第2章：研究目的をどれだけ明確にできるのかが重要
第3章：p値で結果が左右される時代は終わりました
第4章：多くの人が統計を苦手にする理由
第5章：統計を使えるようになるために今日から何をすれば良いか？
第6章：統計を学ぶために重要な環境
もしあなたがこれまでに、何とか統計をマスターしようと散々苦労し、何冊もの統計の本を読み、セミナーに参加してみたのに、それでも統計が苦手なら…
私からプレゼントする内容は、あなたがずっと待ちわびていたものです。
