「ある治療を行った結果、どれくらいの効果があったのか?」
臨床研究でこの問いに答える際、単純な平均値の比較だけでは正しい答えにたどり着けないことがよくあります。そこで重要になる指標が「平均因果効果」です。
しかし、この平均因果効果には「ATE(全集団)」と「ATT(介入群)」という2つの異なる種類があり、どちらを見るべきか迷う方も多いのではないでしょうか。
この記事では、因果推論の基礎から、ATEとATTの決定的な違い、そしてそれらを正しく推定するための「傾向スコア分析(IPW法・マッチング)」について、専門的な知識をわかりやすく噛み砕いて解説します。
平均因果効果とは?因果推論の基礎知識
平均因果効果(Average Treatment Effect)を理解するためには、まず「なぜ普通に比較してはいけないのか」という前提を知る必要があります。
原因と結果の差を見る「反事実」モデル
「効果」とは何でしょうか? 統計学の権威であるルービンの因果モデルでは、以下のように定義されます。
効果 = (ある人が介入を受けた結果) − (その人がもし介入を受けなかった場合の結果)
しかし現実世界では、一人の人間が同時に「介入を受けた状態(事実)」と「受けなかった状態(反事実)」の両方を体験することは不可能です。これを「因果推論の根本問題」と呼びます。
個人の効果を観測することは不可能であるため、集団単位で平均をとって推測しようというのが「平均因果効果」の考え方です。
なぜ単純な比較ではダメなのか?「交絡因子」とバイアス
例えば、「高血圧の人ほど年収が高い」というデータがあったとします。これを見て「高血圧になれば年収が上がる」と考えるのは間違いです。
実際には、以下のような背景(交絡因子)が隠れています。
- 年齢が高い → 血圧が高くなりやすい
- 年齢が高い → 年収が高くなりやすい
このように、結果(年収)と原因(高血圧)の両方に影響を与える第三の要因を「交絡因子(こうらくいんし)」と呼びます。
観察データ(単に集めただけのデータ)にはこの交絡バイアスが含まれているため、単純なグループ比較では純粋な「効果」が見えなくなってしまうのです。
【重要】ATE(全集団)とATT(介入群)の違いと使い分け
交絡因子を取り除き、純粋な効果を測る指標として、主に以下の2つが使われます。この2つの使い分けが、分析設計の要(かなめ)となります。
ATE(Average Treatment Effect):集団全体に施策を行ったら?
ATE(全集団の平均因果効果)は、対象となる集団全員が、もしその施策を受けたら(または受けなかったら)、平均的にどれくらいの効果差が出るかを示す指標です。
- 定義: 集団全体における「介入あり」と「介入なし」の平均的な差。
- 向いているケース:
- 社会全体への政策導入(例:国民全員に新しいワクチンを打つべきか?)
- 全顧客へのキャンペーン(例:全ユーザーにクーポンを配布したら売上はどうなるか?)
「もし全員に適用したらどうなるか?」という未来の全体最適を考える際に用いられます。
ATT(Average Treatment Effect on the Treated):実際に受けた人の効果は?
ATT(介入群の平均因果効果)は、実際に施策を受けた人たち(介入群)にとって、その施策がどれくらい効果的だったかを示す指標です。
- 定義: 実際に介入を選択した人たちにおける、「介入あり」と「もし介入を受けていなかったら」の平均的な差。
- 向いているケース:
- 希望者参加型のプログラム(例:禁煙プログラムに参加した人は、参加しなかった場合に比べて禁煙成功率が上がったか?)
- 既存の利用者評価(例:有料プランに加入したユーザーは、加入しなかった場合より利用頻度が高いか?)
「実際に選んだ人にとって意味があったのか?」という事後評価やプログラムの効果検証によく用いられます。
図解でイメージするATEとATTでのターゲット層の違い
この図は、ATEとATTが統計学的に「どの部分の差」を見ようとしているのかを表しています。ここで最も重要なのは、黄色いマーカーで「実際には得られない」と書かれている部分(反事実)の存在です。
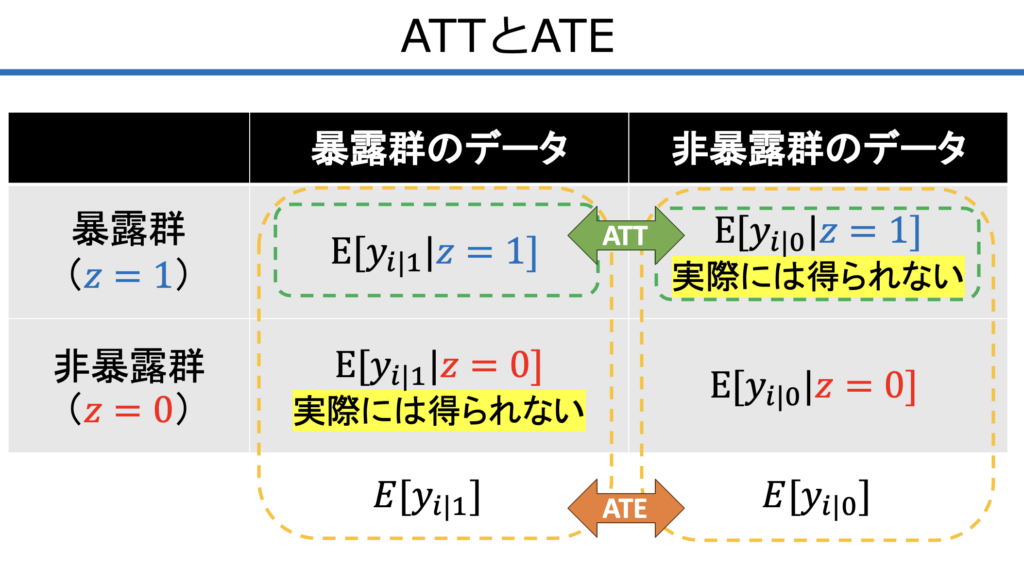
現実世界では、ある人が「介入を受けた結果」と「受けなかった結果」を同時に観測することはできません。そのため、以下の図のように比較のアプローチが異なります。
- ATT(緑の矢印):上段の「暴露群(z=1)」だけに注目します。「実際に介入を受けた人」が、もし受けなかったらどうなっていたか(右上の黄色い部分)を推定し、その差を比較します。
- ATE(オレンジの矢印):上下段を含めた「集団全体」に注目します。暴露群・非暴露群それぞれの「あり得たかもしれない結果(黄色い部分すべて)」を推定し、全体としての平均的な差を比較します。
つまり、「欠損しているデータ(黄色)を、どの範囲まで埋めて比較するか」の違いが、そのままATEとATTの違いになっているのです。
| 指標 | 対象(ターゲット) | 問いかけのイメージ | 推定手法の例 |
| ATE | 全員 (介入群 + 非介入群) | 「もし全員にやらせたら、平均でどうなる?」 | IPW法 (逆確率重みづけ) |
| ATT | 介入群のみ | 「やった人にとって、どれだけ得だった?」 | マッチング法 |
平均因果効果を正しく推定する手法「傾向スコア分析」
観察データから交絡バイアスを取り除き、ランダム化比較試験(RCT)のような状態を擬似的に作り出す手法が「傾向スコア(Propensity Score)」を用いた分析です。
多変量解析と傾向スコア分析の違い
多くの研究で使われる「多変量解析(重回帰分析など)」も交絡因子の調整に使われますが、目的が少し異なります。
- 多変量解析:
- 主に「予測」や「要因の探索」に使われる。
- 「結果Yに対して、要因X1, X2…がどう効いているか」というモデルを作る。
- 傾向スコア分析:
- 純粋に「介入の効果(因果関係)」を知りたい場合に特化している。
- 群に対して、交絡因子をモデル化している。交絡因子をまとめて「傾向スコア(ある人が介入を受ける確率)」という1つの指標に変換し、群間の背景情報のバランスを整える。
「とにかくバイアスを取り除いて、フェアな比較をしたい」という場合には、傾向スコア分析が適しています。
ATEを推定する「IPW法(逆確率重みづけ)」
ATE(全集団の効果)を知りたい場合によく使われるのがIPW法(Inverse Probability Weighting)です。
これは、傾向スコア(介入を受ける確率)の逆数を重みとしてデータに掛ける方法です。
IPW法がどのようにして「公平な比較」を可能にしているのか、データの動きを3つのステップで見てみましょう。
Step1:調整前のデータ(バイアスがある状態)
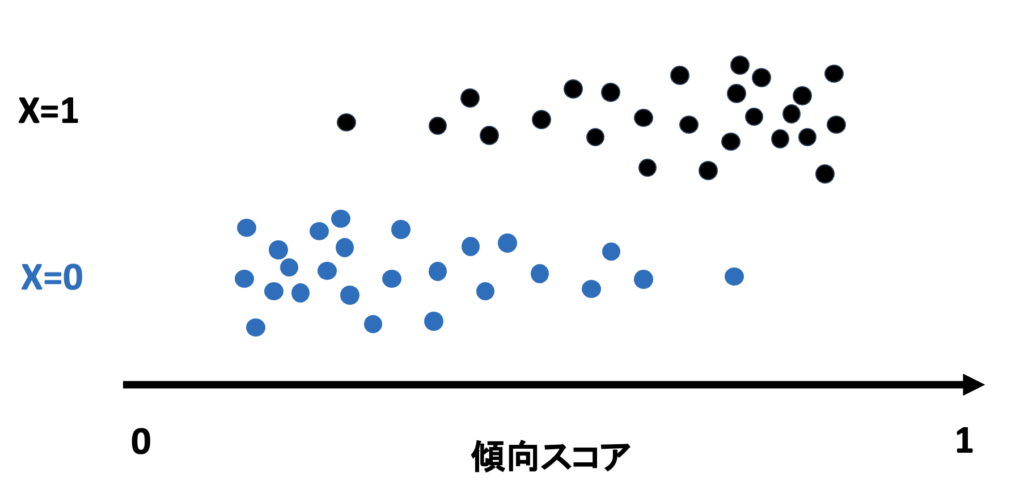
まず、これが現実のデータ分布です。
- 上段(X=1 介入群): 傾向スコアが高い(右側にある)人が多い。
- 下段(X=0 対照群): 傾向スコアが低い(左側にある)人が多い。
このように、傾向スコア(なりやすさ)に偏りがあるため、そのまま比較するとバイアスがかかってしまいます。上下でドットの位置がずれているのが分かります。
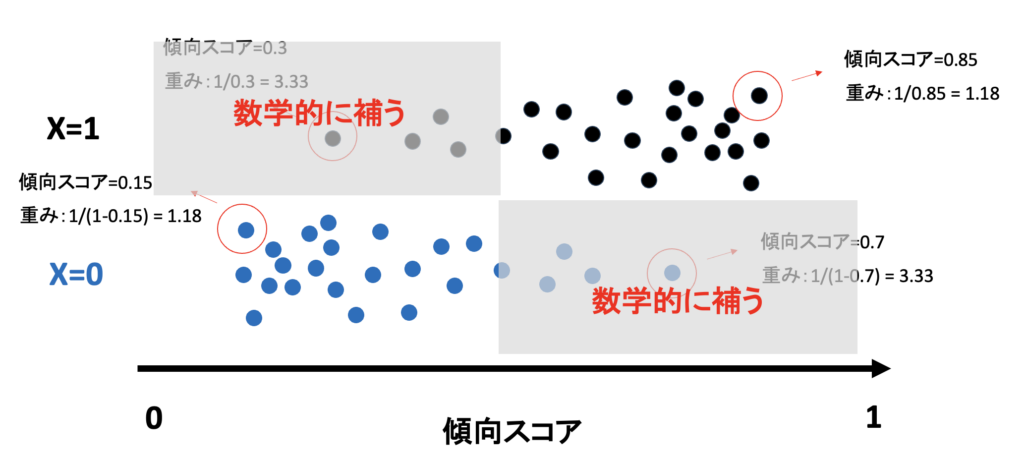
Step 2:目指すゴール(擬似的な集団の作成)
ATE(全集団の平均因果効果)を知るためには、「全員が介入を受けた世界」と「全員が受けなかった世界」を比較する必要があります。
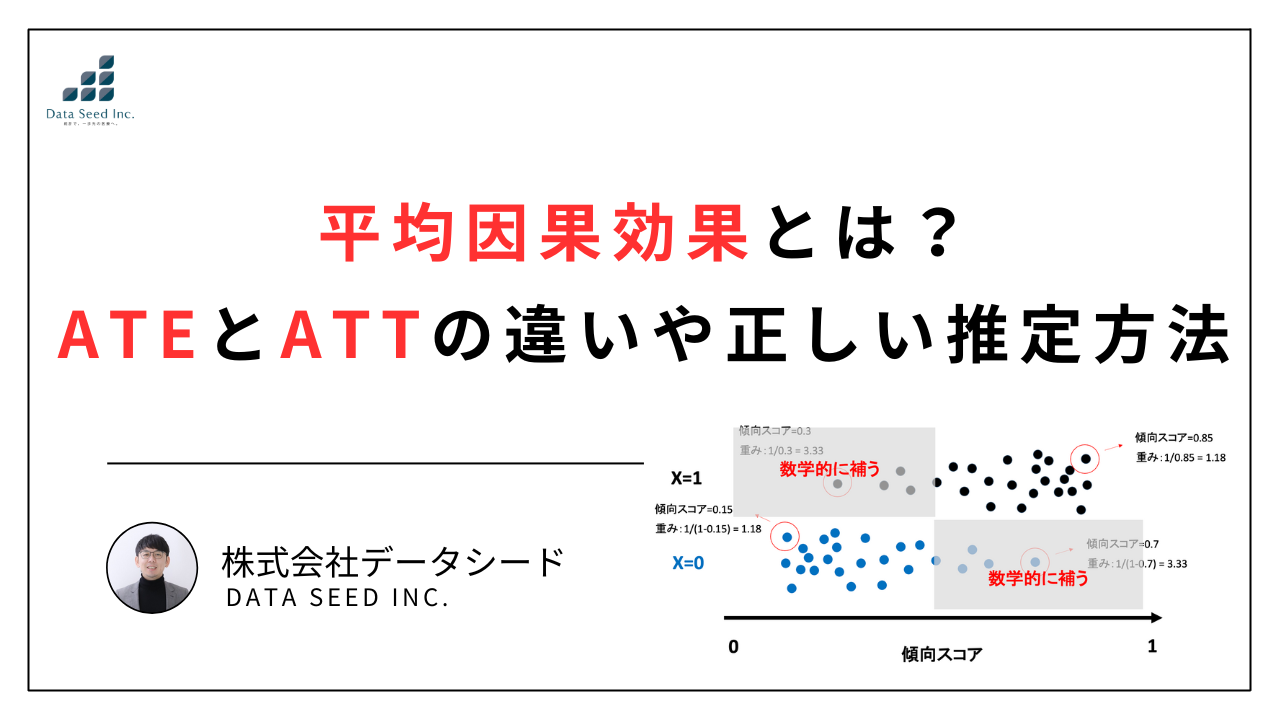
そこでIPW法では、データが足りない部分(薄いグレーの背景部分)を「数学的に補う」という操作を行います。これにより、あたかも全員のデータが揃っているかのような「擬似個体群」を作り出します。
Step 3:具体的な計算方法(重みの付与)
では、具体的にどうやって「補う」のでしょうか? ここで「逆確率による重みづけ」が登場します。
- レアな人ほど、重みを大きくする:例えば、X=1(介入群)の中に、傾向スコアが0.3と低い(本来なら介入を受けにくい)人がいたとします。この人は「レアな存在」です。そこで、確率の逆数(1/0.3)を計算し、この1人のデータを「3.33人分」に膨らませて扱います。
- よくいる人は、重みを小さくする:逆に、傾向スコアが0.85と高い(介入を受けて当然の)人は、逆数(1/0.85)となり、重みはあまり増えません。
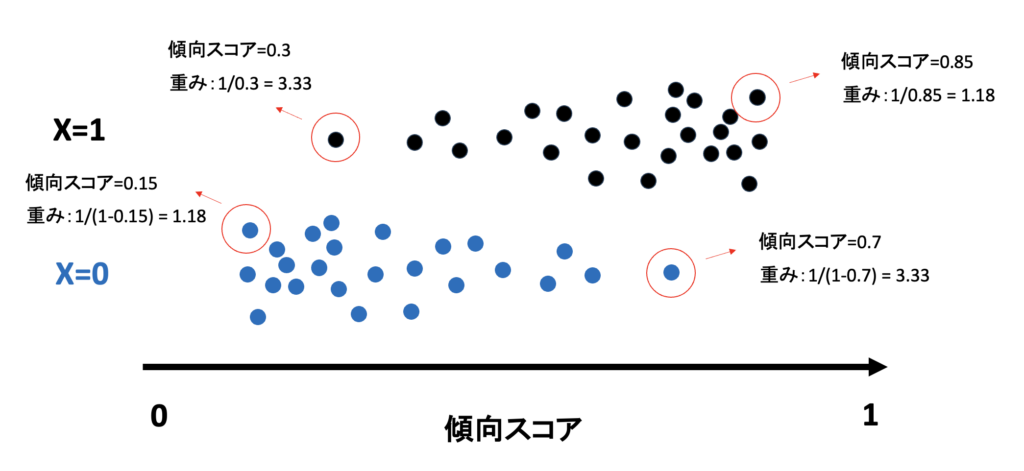
このように「起こりにくいこと(逆確率)ほど重視する」ことで、擬似的に全体のバランスを整え、公平な平均因果効果(ATE)を算出可能にするのです。
- 介入を受けにくいのに受けた人(レアな人)の重みを大きくする。
- 介入を受けやすいのに受けた人(よくいる人)の重みを調整する。
これにより、擬似的に「介入群」と「対照群」の人数や背景因子のバランスが取れた全集団(擬似個体群)を作り出し、全体での効果を推定します。
ATTを推定する「マッチング法」
ATT(介入群の効果)を知りたい場合によく使われるのがマッチング法(傾向スコアマッチング)です。
これは、介入群の一人ひとりに対し、傾向スコア(背景情報)が非常によく似た「介入を受けなかった人」を探してきてペアを作る方法です。
- ペアにする条件: 性別、年齢、年収などの背景がそっくりな人同士。
- 比較: 似たもの同士のペアで結果を比較する。
ペアにならなかった(似た相手がいなかった)データは捨てられるため、集団全体(ATE)の評価には向きませんが、介入群とそっくりな人を比較対象にするため、介入群における純粋な効果(ATT)を高精度に推定できます。
まとめ:研究目的に合わせて適切な平均因果効果を選ぼう
「平均因果効果」を分析する際は、ご自身の目的がどこにあるかを明確にすることがスタート地点です。
- 政策や全体戦略を決めたいなら → ATE(全集団の平均因果効果)
- 手法:IPW法など
- 特定の施策の効果検証をしたいなら → ATT(介入群の平均因果効果)
- 手法:マッチング法など
適切な指標と手法を選ぶことで、バイアスに惑わされない、真のデータ活用が可能になります。












コメント