群間比較した効果を調べるときに、共変量による結果へのバイアスが生じる可能性があります。
そのため、計画段階から共変量のバイアスを小さくする方法として、ランダム化（無作為化）比較試験があります。
しかし観察実験では、ランダム化ができない場合があります。
ランダム化ができない場合に共変量のバイアスを小さくする方法として、傾向スコアマッチング法が考案されています。
今回の記事では、傾向スコアマッチング法について解説していきます。
Contents
傾向スコアマッチング法（プロペンシティスコアマッチング法）とは？
傾向スコアマッチング法は英語では、Propensity Score Matching Methodsといいます。
他にも、Propensity Analysisと呼ばれるときもあります。
傾向スコアマッチング法は共変量によるバイアス（交絡バイアス）を小さくするために用いられる手法です。
臨床試験などの介入研究では、ランダム化（無作為化）比較試験によって共変量によるバイアスを小さくすることができます。
フィッシャーの三原則でも、ランダム化が重要であることが述べられています。
しかし、観察研究では、無作為化比較試験のような操作を行うことはできません。
そこで。
傾向スコアマッチング法は主に観察実験の際に、共変量によるバイアスを小さくするために用いられます。
傾向スコアマッチング法に関する語句の説明
傾向スコアマッチングではいくつかの語句が出てくるので、まずは語句を説明していきます。
傾向スコアマッチングの用語：アウトカム
これは、要素に対する結果に当たります。
例えば、治癒の有無や、死亡、生存時間などが当てはまります。
傾向スコアマッチング法では1つのアウトカムについて扱います。
傾向スコアマッチングの用語：割り当て変数
名義尺度またはカテゴリーデータのことです。
傾向スコアマッチング法では、2つの水準を用いることが一般的です。
例えば、曝露群と非曝露群、摂取群と非摂取群などが当てはまります。
傾向スコアマッチング法では1つの割り当て変数について扱います。
傾向スコアマッチングの用語：共変量
これは、割り当て変数に分けれた群に共通して存在する変量です。
例えば、性別、体調、病気の重症度、年齢などが当てはまります。
傾向スコアマッチング法では1つ以上の割り当て変数について扱います。
傾向スコアマッチングはどんな状況の時に使えばいい？
傾向スコアマッチング法は、観察実験において用います。
前述の通り、観察研究の場合にはランダム化をすることができないからです。
ランダム化の恩恵は、例えば比較する群が2つだった場合に、2群間で同じような集団を作ることができるという点が、ランダム化の素晴らしい点です。
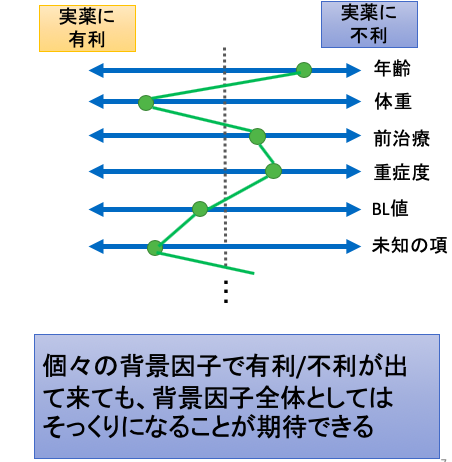
例えば、新しい抗がん剤が既存の薬剤に比べて効果があるかどうかを知りたい時、2群間で病気の重症度が異なっていたらどうでしょうか？
新しい抗がん剤治療を選択する人は重症度が高い患者さんが多く、既存の薬剤を選択する人は軽症な場合が多い時には、どれだけ新しい抗がん剤が優れていたとしても、効果がないという結果が出る可能性があります。
それを防ぐ方法として、傾向スコアマッチング法を使って、あたかも2群間で同じような集団を作り上げることができるのです。
例として、「妊娠中の女性がフェノバルビタールを摂取したときの、胎児の知能への影響を調査した研究」を紹介します。
目的は、妊娠中の女性がフェノバルビタールを摂取したときの、胎児の知能への影響の有無です。
この事例のとき、アウトカムは胎児の成長後の知能です。
割り当て変数は、フェノバルビタールの処方の有無が推定します。
薬を処方した群と処方してない群には、それぞれ様々な胎児への知能に関係する共変量が存在しています。
この事例では、社会経済的地位や、父親の有無などが共変量として用いられています。
目的などをまとめておきますね。
- 目的：妊娠中の女性がフェノバルビタールを摂取した時の、胎児の知能への影響の有無
- アウトカム：胎児の成長後の知能
- 割り当て変数：フェノバルビタールの処方の有無
- 共変量：社会経済的地位、父親の有無など
傾向スコアマッチング法は具体的にどうする?
傾向スコアマッチング法は、次のような流れで行います。
- 共変量の選択
- 傾向スコアの推定
- 傾向スコアの利用
- バランスの評価
- 効果の推定
- 効果の解釈
傾向スコアマッチングの手順：共変量の選択
共変量は、割り当て変数に対応する操作の前の変数か、同時に測定された変数を利用します。
ここで共変量には、アウトカムを含めることはできませんし、割り当て変数によって変化しうる変数を選択することはできません。
具体的な共変量の選択には、先行研究の内容や、統計解析を参考に選定を行います。
傾向スコアマッチングの手順：傾向スコアの推定
傾向スコアは、共変量が与えられた条件下で、その人がある群にあてはまる確率のことです。
傾向スコア推定の方法は一つではななく、ロジスティック回帰分析や、ニューラルネットワーク、判別分析などが用いられます。
私が見かけることが多いのは、ロジスティック回帰分析ですね。
ロジスティック回帰分析でプロペンシティスコアマッチング法を具体的にどうやるかというと、以下の式で得られる確率を求めます。
割り当て変数＝ logit ( 共変量1 + 共変量2 + 共変量3 + ・・・)
この計算で得られた確率をもとに、マッチングしていきます。
傾向スコアマッチングの手順：傾向スコアの利用法
傾向スコアの利用法もいくつか存在します。
- マッチング
- 層化
- 重み付け
- 共変量
などです。
マッチング法では、
片方の群から無作為に一人を選択し、もう一方の群から選択した人の傾向スコアと最も似た傾向スコアの人の人とペアをつくります。
そして、この方法を反復して行なっていきます。
これを行うことによって、できるだけ似た共変量を持った者同士での比較を行うことができるため、共変量のバイアスが小さくなります。
傾向スコアマッチングの手順：バランスの評価
これもいくつかの方法がありますが、標準化差という手法がよく用いられます。
これは、先ほどマッチングで作ったものにバランスが取れているか、(バイアスは小さくなっているか)を確認するために用います。
傾向スコアマッチングの手順：効果の推定
効果の推定にはT検定はカイ二乗検定、比例ハザードモデルなどを利用します。
T検定とは？帰無仮説と対立仮説を必ず確認！F検定で等分散の確認が必要？
カイ二乗検定とは？計算式まで簡単に分かりやすく！分割表の検定
これらの解析では従属変数をアウトカム、独立変数を割り当て変数と共変数を用いておこなます。
傾向スコアマッチングの手順：効果の解釈
結果の解釈には平均因果効果をいうものが用いられます。
平均因果効果（Average Causal Effect）は、母集団のすべたが、一方の群に移ったときの、アウトカムの期待値差と定義されます。
傾向スコアマッチングのデメリット
ランダム化していない観察研究でも、まるでランダム化したかのように扱える傾向スコアマッチングは、一時期とても話題になりました。
しかし傾向スコアマッチングにはデメリットもありますので、ぜひ使う際にはデメリットも意識して使いましょう。
傾向スコアマッチングのデメリットは大きく分けて二つ。
傾向スコアマッチング後のデータ数は得られているデータ数より必ず小さくなる
まず、傾向スコアマッチングは「マッチング」なので、似ているデータがある時には採用されますが、そうでなければデータは採用されません。
そのため、傾向スコアマッチング後のデータ数は、現在手元にあるデータ数よりも必ず小さくなります。
例えば合計で100例分のデータがあったとして、傾向スコアマッチング後には50例分のデータしか使えない、といった状況になります。
それを回避する方法としては、傾向スコアを使ったIPTW法もありますが、直感的にわかりにくい方法でもあり、あまり使われていない印象があります。
データとして得られている共変量でしかマッチングできない
傾向スコアマッチングは、ランダム化していないデータであっても、まるでランダム化したかのように扱える、ということで話題になりました。
しかしそれには落とし穴があります。
傾向スコアマッチングで考慮できるのは、あくまでデータとして取得した共変量のみです。
傾向スコアを算出する共変量として扱っていないデータに対しては交絡バイアスを排除できません。
一方のランダム化は、未知の因子であっても、データ化されていない因子であっても、群間で平均的に似通った集団を作る、ということに最大のメリットがあります。
この点はランダム化と傾向スコアマッチングで大きな違いですので、傾向スコアマッチングの限界は知っておきましょう。
傾向スコアマッチング法まとめ
傾向スコアマッチング法は共変量によるバイアスを小さくするために用いられる手法です。
傾向スコアマッチング法は主に観察実験の際に、共変量によるバイアスを小さくするために用いられます。
第1章：医学論文の書き方。絶対にやってはいけないことと絶対にやった方がいいこと
第2章：先行研究をレビューし、研究の計画を立てる
第3章：どんな研究をするか決める
第4章：研究ではどんなデータを取得すればいいの？
第5章：取得したデータに最適な解析手法の決め方
第6章：実際に統計解析ソフトで解析する方法
第7章：解析の結果を解釈する
もしあなたがこれまでに、何とか統計をマスターしようと散々苦労し、何冊もの統計の本を読み、セミナーに参加してみたのに、それでも統計が苦手なら…
私からプレゼントする内容は、あなたがずっと待ちわびていたものです。
[…] 現状、標準化差は傾向スコアマッチングの論文でよく見かける指標です。 […]