エクセルでエラーバーの出し方はどうする？棒グラフや折れ線グラフで解説！

医療系の論文や学会発表においてグラフを用いたデータの可視化は、自らの主張を分かりやすく伝える上で極めて有用ですね。

属性ごとの記述統計や群比較、経時比較の結果を下記のようなエラーバーグラフで表現しているのを見たことがあるのではないでしょうか。

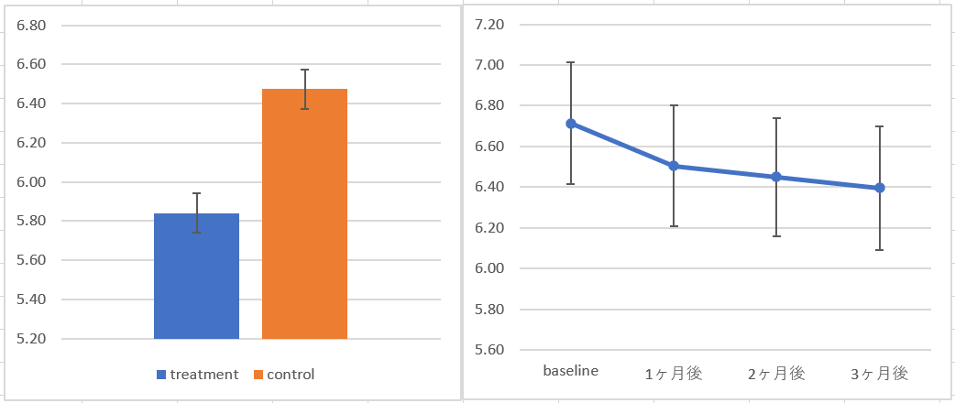
本記事では、このようなエラーバーグラフをExcelで作成する方法について解説していきます。

 

エラーバーとはそもそも何？

グラフの作り方の前に、エラーバーの意味をおさえておきましょう。

エラーバーとは、データの集合が特定の値からどの程度バラついているかを可視化するものです。

もともとは実験における誤差（error）や測定の不確かさを表現するために考案されたものと言われています。

 

特定の値については「平均値」を用いるのが一般的です。

 

エラーバーの種類：標準偏差や95%信頼区間

グラフの基準点となる平均値から伸びるヒゲがエラーバーですが、このエラーバーの長さの決め方には3種類あります。

 

その3種類とは

1. 標準偏差
2. 標準誤差
3. 95%信頼区間

です。

 

論文や発表の前半で、被験者全体の分布を表現するような、データそのものを表現する場合には標準偏差を用います。

それに対し、統計分析の結果として平均値などの推定値の精度をエラーバーグラフで表示する場合には標準誤差や95%信頼区間を用います。

なかでも、95%信頼区間を用いると、有意差の有無を可視化することができます。

 

これら3種類のエラーバーの使い分けは厳密に決められているわけはありません。

ジャーナルによっては投稿規定で指示される場合もありますが、そのような指示がなく、どのエラーバーを用いるか迷うようなときは、投稿先の他の論文等を参考にするのが良いでしょう。

 

エクセルで棒グラフと折れ線グラフへのエラーバーの出し方

では、エラーバーグラフをExcelで作ってみましょう。

まずは、群比較に代表されるエラーバー付き棒グラフです。

 

ある介入試験により以下の結果が得られているとします。

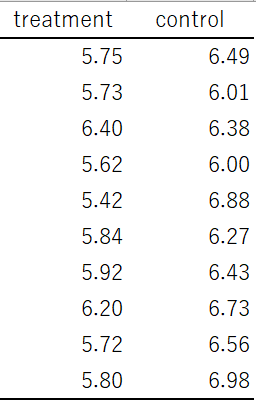
エクセルでのエラーバー作成の準備：各値の計算

エラーバー付き棒グラフ作成に必要な平均値、標準偏差、標準誤差、95%信頼区間を順次計算していきます。

標準誤差や95%信頼区間の計算に必要になるため、COUNT関数でサンプル数を求めます。

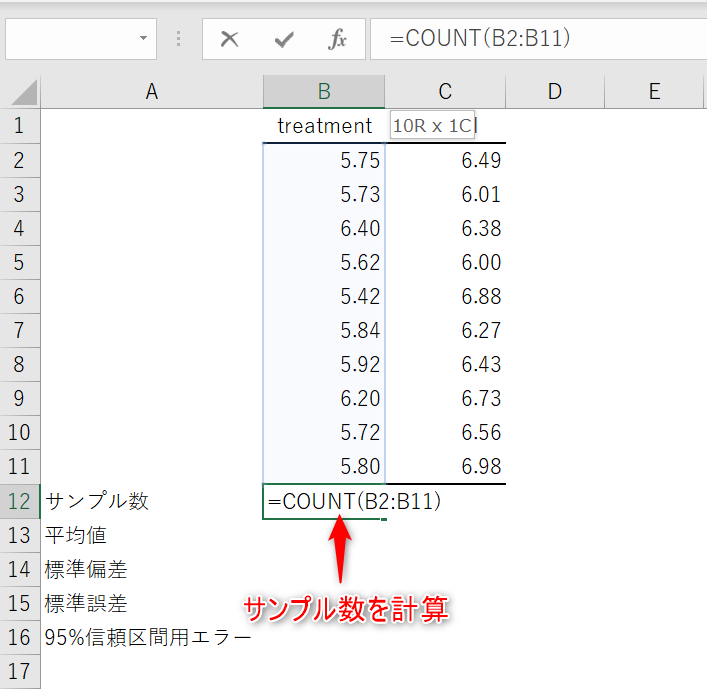
AVERAGE関数で平均値を計算。

STDEV.P関数で標準偏差を計算。

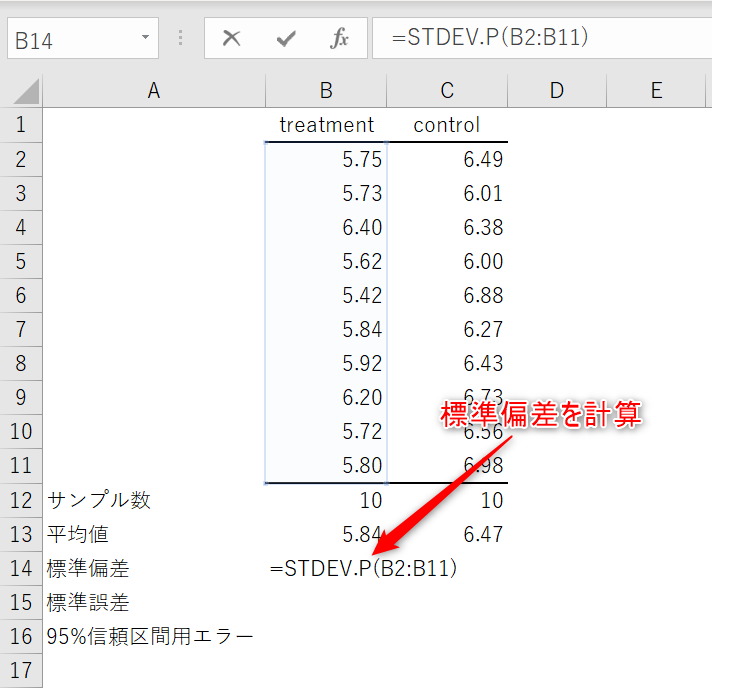
STDEV.S関数と平方根を求めるSQRT関数、上で求めたサンプル数を組み合わせて標準誤差を計算。

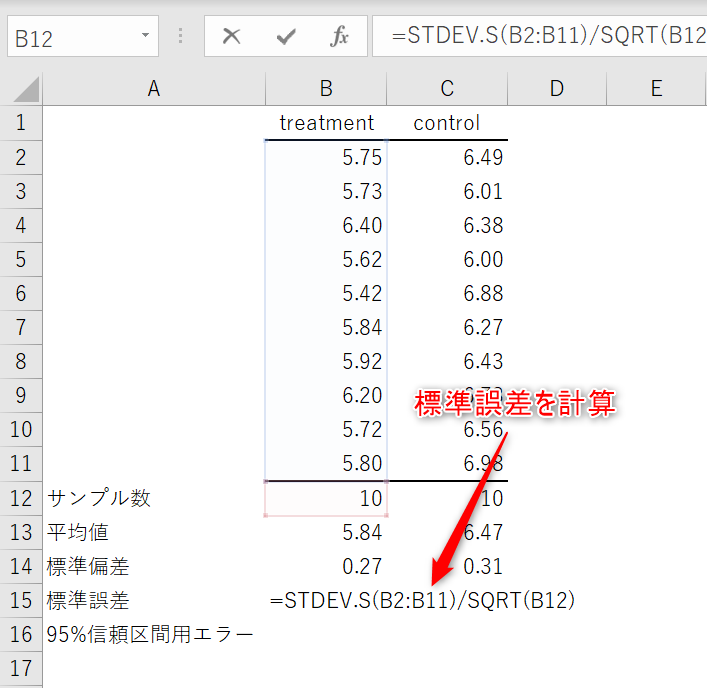
標準誤差とt分布のT.INV.2T関数を用いて95%信頼区間用のエラーバーを計算。

95%信頼区間の場合は確率を0.05、自由度をサンプル数から1引いた数に設定。

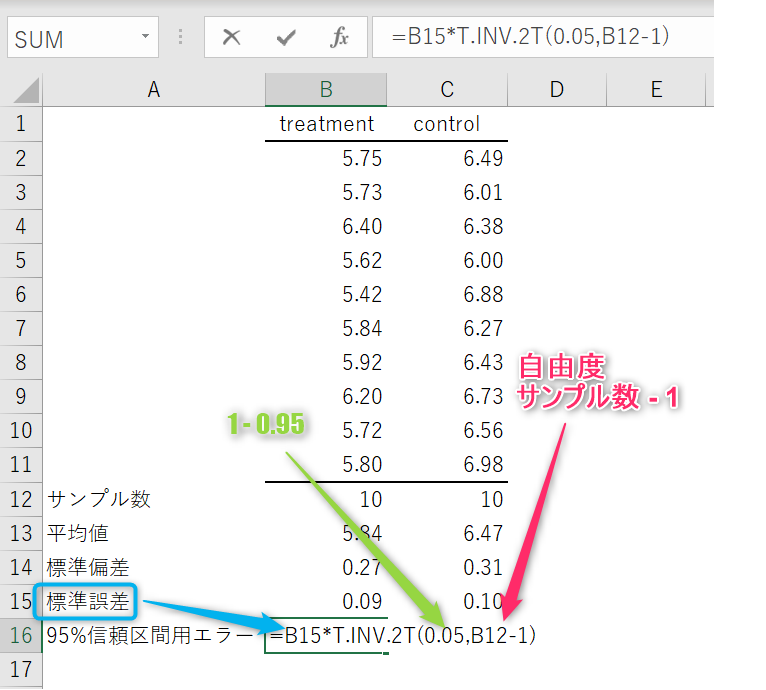
これで準備完了です。

エラーバー付き棒グラフの作成に移りましょう。

 

エクセルでエラーバー付き棒グラフの作成方法

まず、グループ名と平均値を範囲指定します。

そして、「挿入」タブから棒グラフのアイコンを選び、「その他の縦棒グラフ」を選択。

グループごとに色分けされているグラフを選択します。

グラフ要素の「誤差範囲」をチェックして「その他のオプション」をクリック。

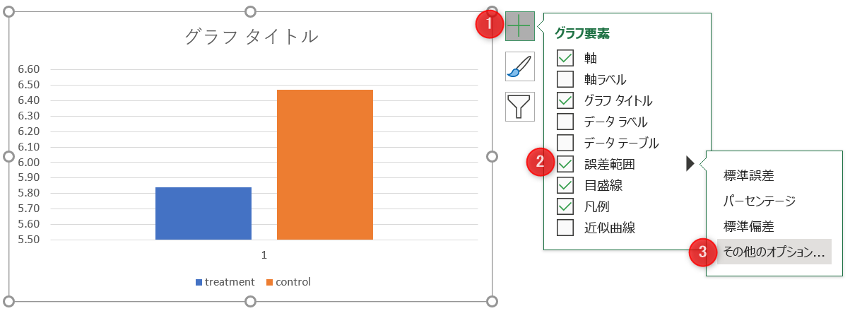
エラーバーをつける系統を選択。

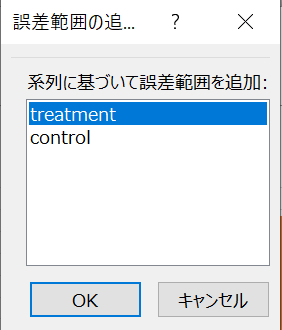
誤差範囲から「ユーザー設定」をチェックして「値の指定」をクリック

ユーザー設定の誤差範囲ウィンドウで「正の誤差の値」「負の誤差の値」それぞれにエラーバーにしたい値を選択。

（この例では標準偏差を選択）

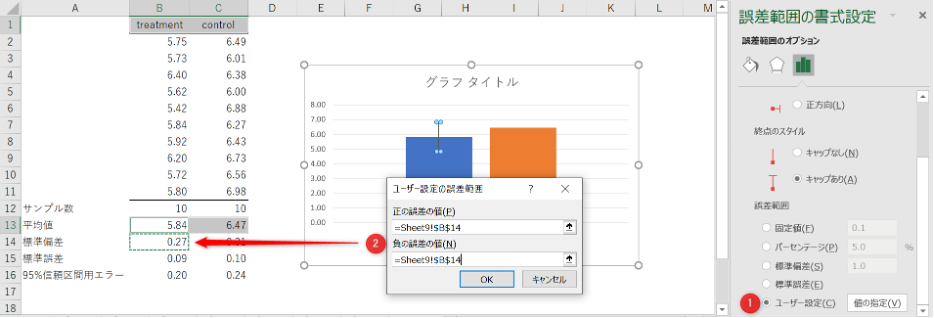
別の系統についても同様に設定すると。

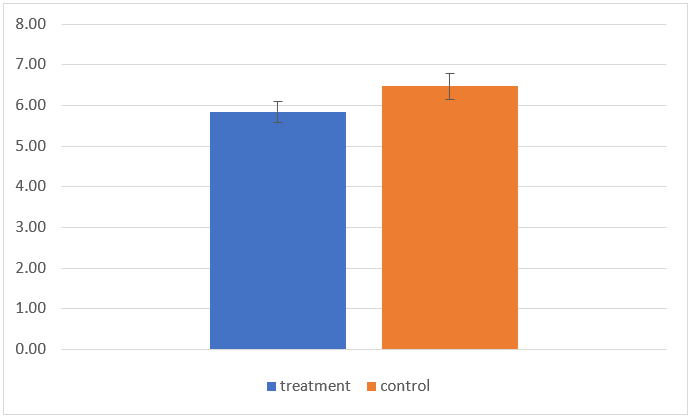
エラーバー付き棒グラフの完成です。

 

エクセルでエラーバー付き折れ線グラフの作成方法

次に、エラーバー付き折れ線グラフの作り方です。

経時測定されたデータなどに最適な可視化になります。

 

ある患者集団を経過観察した結果が以下のようになったとします。

平均値と標準偏差も計算済です。

この結果について、エラーバー付き折れ線グラフを作成します。

 

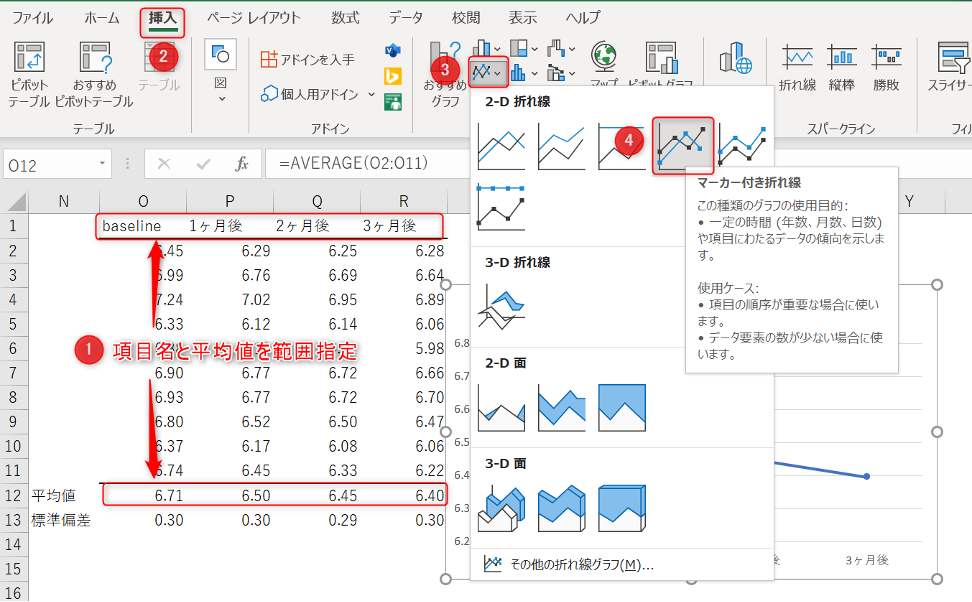
棒グラフのときと同じように項目名と平均値を範囲指定します。

「挿入」タブから折れ線グラフのアイコンを選び、「マーカー付き折れ線」をクリック。

グラフ要素の「誤差範囲」をチェックし「その他のオプション」を選択。

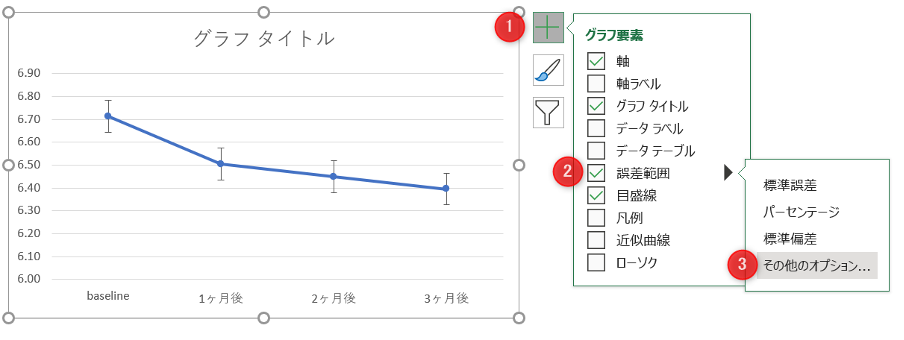
誤差範囲から「ユーザー設定」をチェックして「値の指定」をクリック。

ユーザー設定の誤差範囲ウィンドウで「正の誤差の値」「負の誤差の値」それぞれにエラーバーにしたい値を選択。

（この例では標準偏差）

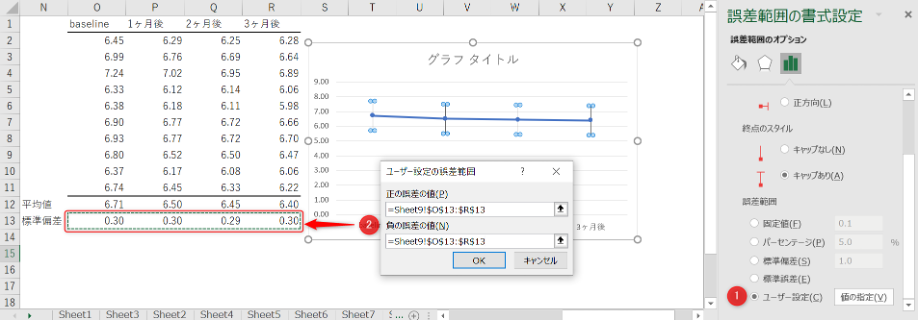
そうすると、エラーバー付き折れ線グラフの完成です。

まとめ

データや分析結果を可視化することは、学会発表や論文において、とても有効ですね。

集団の基準とバラつきを同時に表現できるエラーバー付きグラフは様々なケースで使うことができます。

このエラーバー付きグラフは、別途グラフ作成用のソフトウェアを用意せずともExcelで比較的簡単に作成できます。ぜひ挑戦してみて下さい。

なお、後半の例にあげた経時測定されたデータでは、標準誤差や95%信頼区間の計算が特殊になりますので、反復測定データについてグラフ化するときは気をつけましょう。