この記事では「乱数とは？正規乱数や一様乱数の説明とエクセルでの作り方までわかりやすく」ということでお伝えさせていただきます。
- 乱数ってそもそも何？
- 一様乱数とか正規乱数ってどんなもの？
- 乱数を使ってみたいんだけど、エクセルで簡単にできるの？
- 乱数は具体的にどんな場面で使われる？
といったことを具体的にわかりやすくお伝えしますね！
乱数とはそもそも何？
乱数とはそもそもなんなのでしょうか？
イメージできるようでできない乱数。
調べてみると、いろんな乱数の説明があるようです。
ASCII.jpデジタル用語辞典での乱数の説明
ASCII.jpデジタル用語辞典での乱数の説明を見てみましょう。
ASCII.jpデジタル用語辞典ではこのような説明がなされています。
なんとなく分かるようで分からないなぁ・・・というのが本音かもしれないですね。
ちょっと概念的な説明に終始しているため、イメージがつきづらいところがあります。
ブリタニカ国際大百科事典での乱数の説明
では今度は、ブリタニカ国際大百科事典での乱数の説明を見てみましょう。
ブリタニカ国際大百科事典ではこのように乱数を説明しています。
今度はもうちょっと具体的になりました。
こっちの方がなんとなくイメージつきやすいですかね。
ですが、0〜9という数値しか取り得ないという点では、少々範囲が狭すぎます。
統計における乱数は、もっと範囲が広いので、この説明でもまた不十分なようです。
統計における乱数のイメージ
では、統計において乱数といったらどういう説明をすればいいのでしょうか。
私だったら、以下のように説明するかなと思います。
ASCII.jpデジタル用語辞典での乱数の説明と、ブリタニカ国際大百科事典での乱数の説明のちょうど中間ぐらいなイメージ。
ここで重要なのが「ある範囲の数値」ということと、「事前に決められた確率」という2つ。
どうやら、この2つが決まれば、乱数というのは分かりそうです。
では次に、医療統計でよく用いられる乱数を具体的に考えてみましょう。
医療統計でよく用いられる正規乱数と一様乱数とは
医療統計でよく用いられる乱数は二つあります。
- 正規分布に従う乱数である「正規乱数」
- 一様分布に従った乱数である「一様乱数」
それぞれどんな特徴があるのか、詳しくみていきましょう。
正規乱数とは？
正規乱数とは、正規分布に従った乱数のことです。
正規分布といえば、統計の世界では最も重要と言っていいほどの分布ですよね。
乱数は「ある範囲の数値」と「事前に決められた確率」の二つが重要でした。
正規乱数では、「ある範囲の数値」と「事前に決められた確率」の二つはどうなるでしょうか。
- ある範囲の数値：平均値と標準偏差（SD）が決められたときに、正規分布に従った範囲の数値
- 事前に決められた確率：正規分布の確率密度関数に従った確率
正規分布は平均値と標準偏差（SD）が決まると、その形が一つに決まります。
そのため、平均値と標準偏差は自分で決める必要はありますが、決めてしまえば、どんな正規分布になるのかが決まりますので、値の取りうる範囲も決まることになります。
そして、分布には確率密度関数というものが決められています。
正規分布の確率密度関数をグラフ化すると以下のようになります。
正規分布では一番高い部分が平均値になりますので、正規分布付近の値の生じる確率は高く、そこから左右対称に生じる確率は小さくなっていきます。
正規乱数では、この確率に従って乱数が発生されるということです。
一様乱数とは？
一様乱数とは、一様分布に従った乱数のことです。
正規乱数の場合と同じように、一様乱数でも「ある範囲の数値」と「事前に決められた確率」の二つを考えていきましょう。
- ある範囲の数値：自分で決めたa〜bの範囲で
- 事前に決められた確率：一様分布の確率密度関数に従った確率
例えばa=1、b=6と決めると、その確率密度関数をグラフ化すると以下のように。
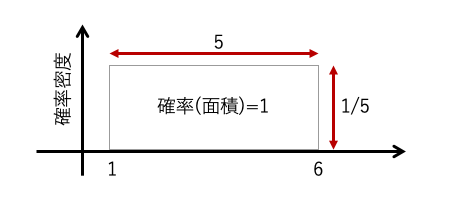
一様分布は、a〜bの中での発生確率は同じ（一様である）という分布なので、 この生じる確率に従って乱数が発生する、ということです。
エクセルでも簡単に乱数が使える
今まで見てきた乱数を、今度はエクセルで実践してみましょう。
エクセルでも簡単に乱数が使えてしまいます。
エクセルで乱数を発生させる関数は「=rand()」です。
実際の使い方の例を見ていきましょう。
エクセルで正規乱数を発生させる
=rand()を使って、正規乱数を発生させてみます。
具体的には、「平均＝0、SD=1」の正規分布に従う値を出力させてみます。
正規分布をエクセルでグラフ化！という記事でも用いた関数そのままです。
=NORM.INV(RAND(),0,1)
RAND()の部分が、乱数を発生させている部分になります。
で、平均が０、標準偏差が１を入力しています。
上記の関数で1つのデータが発生します。
A1に=NORM.INV(RAND(),0,1)と入っていますね。
それを、今回は30個のデータを発生させます。
そのため、A１の関数をコピペして30個データを発生させましょう。
RAND()はセルによって常に値が変わります。
そのため、何も考えずにコピペすることで異なる30個のデータが作成できます。
そして、この30個のデータに対して平均と標準偏差を計算してみるのです。
そうすると今回のデータでは、平均が-0.04、標準偏差が1.08というデータだったことがわかります。
「平均＝0、SD=1」の正規分布に従う値を出力させているので、ちゃんと意図通りのデータになっていることがわかりますね。
乱数はどんな場面で使われるの？
乱数そのものもわかったし、エクセルでも簡単に乱数を使うことができることもわかった。
じゃあ、その乱数ってどこで使えるの？という疑問が出てきます。
医療統計で乱数は主に「シミュレーション」の場合に使われることが多いです。
特に、サンプルサイズ設計の時のシミュレーションですね。
EZRやJMPやSPSSなどの統計ソフトでもサンプルサイズは計算できるのですが、あくまでも検定ベースのサンプルサイズしか計算できません。
例えば、T検定に基づくサンプルサイズ設計、カイ二乗検定に基づくサンプルサイズ設計、などです。
しかし、検定よりも、もうちょっと複雑な条件（多変量解析など）でサンプルサイズ設計をしたいという場面が出てきます。
そのときに、シミュレーションを使って擬似的にデータを発生させ、サンプルサイズ設計をするという使い方をすることが多いです。
まとめ
いかがでしたか？
この記事では「乱数とは？正規乱数や一様乱数の説明とエクセルでの作り方までわかりやすく」ということでお伝えさせていただきました。
- 乱数ってそもそも何？
- 一様乱数とか正規乱数ってどんなもの？
- 乱数を使ってみたいんだけど、エクセルで簡単にできるの？
- 乱数は具体的にどんな場面で使われる？
といったことがわかったのなら幸いです！
こちらは動画でも解説していますので、併せてご確認くださいませ。
コメント