標準偏差と分散の関係や違いとは？データの単位と同じ次元はどっち？

データのバラツキを表すパラメーターである”標準偏差”。

しかし標準偏差と同様に、統計では”分散”というもう一つのデータのバラツキを表すパラメーターが出てきます。

バラツキを表すパラメータとして、分散と標準偏差は何が違うのでしょうか？

この記事では、分散と標準偏差の関係と分散と標準偏差の求め方について説明します。

 

分散と標準偏差の関係とは？

標準偏差と分散はどちらもデータのバラツキを表すパラメーター（指標）です。

標準偏差と分散の関係は、次のような関係があります。

(標準偏差)²=分散

そのため、標準偏差と分散の性質は非常によく似ています。

 

標準偏差とは?

“標準偏差”は一言で言うならば、データのバラツキを表すパラメーターです。

そのため、標準偏差には次のような特徴があります。

• 標準偏差が小さい　→ 平均に近いデータが多い　→データのバラツキが小さい
• 標準偏差が大きい　→ 平均から離れたデータが多い　→データのバラツキが大きい

詳しくは、正規分布とは？簡単にわかりやすく標準偏差との関係やエクセルでのグラフ化を解説の記事で紹介しています。

次に、分散について説明していきます。

 

分散とは?

分散も、標準偏差と同様にデータのバラツキを表すパラメータです。

そのため、分散にも標準偏差と同様に次のような特徴があります。

• 分散が小さい　→ 平均に近いデータが多い　→データのバラツキが小さい
• 分散が大きい　→ 平均から離れたデータが多い　→データのバラツキが大きい

 

分散と標準偏差の関係

分散と標準偏差との関係を再度確認してみましょう。

分散と標準偏差には、次のような関係がありましたね。

(標準偏差)²=分散

標準偏差ですが、分散から求めるしか計算方法がありません。

そのため、標準偏差を求めるには、先に分散を求める必要があります。

次に分散と標準偏差の計算方法を見ていきます。

 

分散と標準偏差の求め方

分散と標準偏差は次のように求めることができます。

• 分散：”各データと平均の差の2乗”の平均
• 標準偏差：分散の平方根（ルート）

詳しく見ていきましょう。

分散の求め方

分散は”各データと平均の差の2乗”の平均として求めることができます。

これを数式で表すと、次の式になります

具体的な計算方法は下のように行います。

1. 平均を計算する。
2. 各観測データから平均を引く。
3. “各観測データから平均を引いた値”を2乗する。
4. “各観測データから平均を引いた値を2乗した値”をすべて足し合わせる。
5. 最後に観測データの数で割る。

結構手順が多く、計算がめんどくさいですね。

どうして、このような計算方法をとるのでしょうか。

次に、説明していきます。

分散の考え方

分散の計算が少しややこしいのは、

1. データのバラツキを正確に表せる
2. 数学的に計算が楽である

という理由があるからです。

 

このことを、分散の考え方から説明していきます。

データのバラツキをどう評価したら良いかを考えてみます。

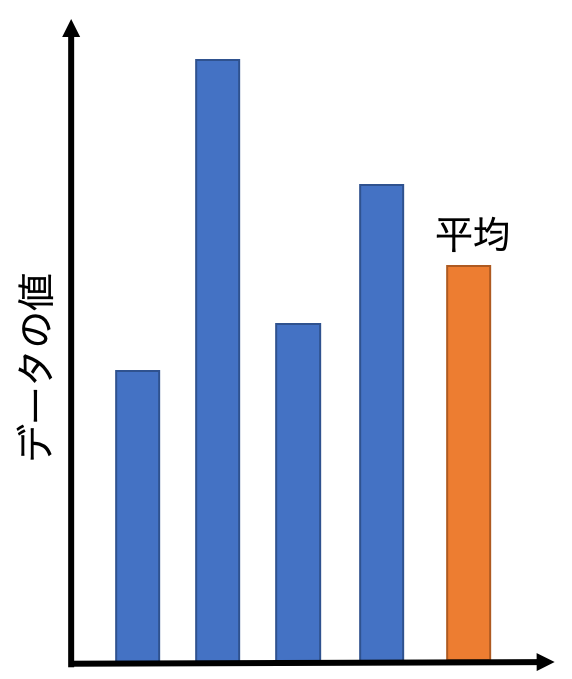
このようなデータがあるとします。

このグラフでオレンジは平均で表しています。

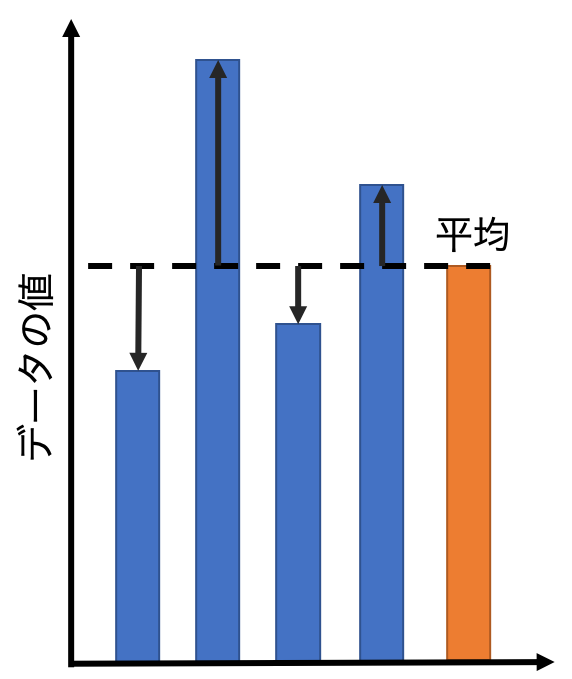
このとき、バラツキに対応するのは、データと平均の差（→）の部分です。

ちなみにデータと平均の差（→）のことを偏差と言います。

バラツキの評価するには、データと平均の差（→）を合計すればできます。

 

このデータと平均の差（→）をどのように合計したら良いのでしょうか。

一番簡単な方法は、

• バラツキ（→）を全て足し合わせる

ことです。

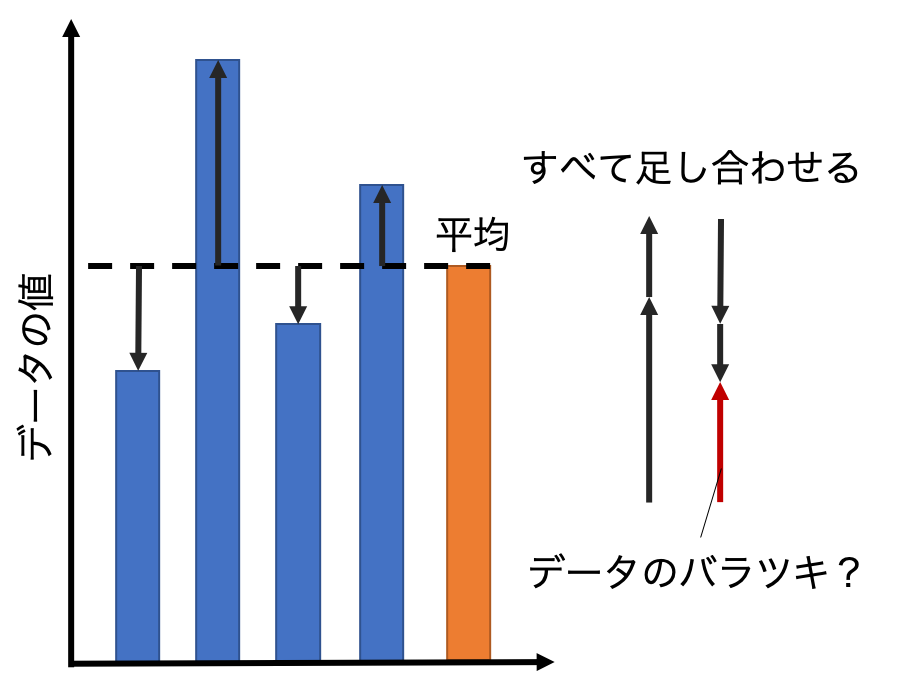
しかし、この方法には問題があります。

それは、データと平均の差には正の数と負の数の両方があります。

そのため、ただ足し合わせるだけだと、正の数と負の数が互いに打ち消し合ってしまうため、バラツキは本来の値よりも小さくなってします。

極端な場合では、正方向の差と負方向の差が等しいとき、バラツキが0になってしまうこともあります。

バラツキがあって、計算しているのに、バラルキが0になってしまうのはおかしいですよね。

次の方法は、

• バラツキ（→）の”絶対値”を全て足し合わせる

ことです。

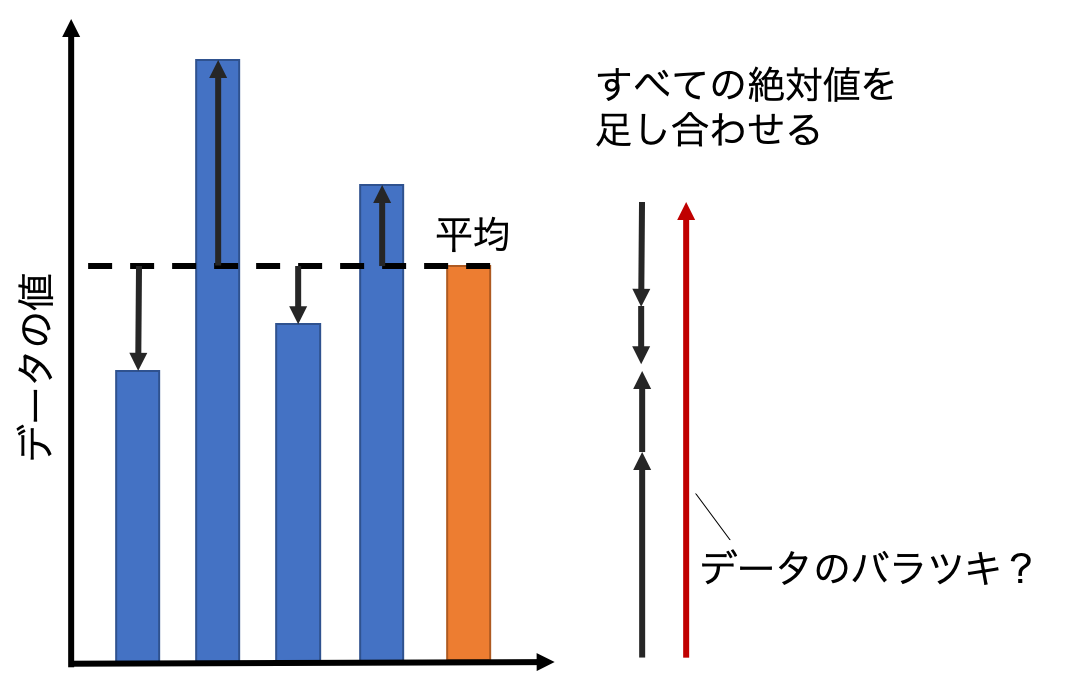
この方法は、さっきのすべてを足し合わせるよりも、データのバラツキを正確に表すことができています。

しかし、絶対値の計算は正の数と負の数を場合分けして考える必要があります。

そのため、数学的に面倒であるというデメリットがあります。

 

そのため、分散ではデータのバラルキの評価に

• バラツキ（→）の2乗を全て足し合わせる

という方法が用いられています。

 

分散の計算が少しややこしいのは、

1. データのバラツキを正確に表せる
2. 数学的に計算が楽である

という理由があるからです。

 

標準偏差の求め方

標準偏差の求め方は簡単です。

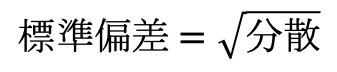
分散の平方根をとるだけです。

平方根をとる理由は、分散を計算するときに、データと平均の差を2乗したので、

これをもとに戻すです。

 

標準偏差の名前

標準偏差という名前は、データと平均の差を偏差ということに由来します。

データと平均の差の2乗は、つまり、偏差の2乗です。

偏差の2乗の平均が、分散です。

ここから、平方根により2乗を外したもののが、”標準”偏差です。

 

さて、標準偏差と分散の計算方法をみました。

 

分散と標準偏差の違い：平均値と同じ次元なのはどっち？

ここまで分散と標準偏差の計算方法についてみてきました。

• 分散：”各データと平均の差（偏差）の2乗”の平均
• 標準偏差：分散の平方根（ルート）

ここから違いを説明していきます。

 

分散は、各データと平均の差（偏差）の2乗です。

そのため、分散は実際のデータとは次元が違います。

例えば、テストの点のデータの分散は必ず、(点)²の次元を持ちます。

これでは、平均やデータと直接比較することができません。

 

一方で、標準偏差は実際のデータと同じ次元を持ちます。

例えば、テストの点のデータの標準偏差は必ず、点とデータと次元を持ちます。

 

よって、標準偏差は実際のデータと同じ次元を持つため、バラツキを評価するときは、分散より標準偏差の方が使いやすいです。

これが、標準偏差の方がよく用いられる理由です。

 

 

まとめ

• 分散と標準偏差はどちらもデータのバラツキを表すパラメータです。
• 分散の求め方：”各データと平均の差（偏差）の2乗”の平均
• 標準偏差の求め方：分散の平方根（ルート）
• 標準偏差の方が、実際のデータと同じ次元を持つため使いやすい

＞＞正規分布とは？

＞＞標準正規分布表の見方を徹底解説！

＞＞要約統計量とは？何を出力すればいいの？

＞＞95%信頼区間とは何？1.96の意味とは？

＞＞ヒストグラムとは？

＞＞エクセルで標準偏差はどの関数を使えばいい？