今回の記事では、EZRで多変量解析を実施する具体的な手順をお伝えします。
実際のデータを解析する際には、T検定やカイ二乗検定などの単純な検定だけでなく、共変量を調整するような多変量解析を多く実施することがありますよね。
そのため、今回の記事がそのままあなたの実務に役立つと思います。
この記事では、EZRを用いて多変量解析の一つである、ロジスティック回帰を実施します。
ロジスティック回帰は、応答変数（目的変数）が二値のカテゴリカルデータである場合に使える解析手法です。
では、いってみましょう！
Contents
EZRで多変量解析の一つのロジスティック回帰分析を実施するにはどんな状況であればいい？
まず重要なのが、あなたの手元にあるデータでどの多変量解析を実施するのか！？ということ。
これを知らなければ、実務でデータを解析することができませんよね。
どの多変量を実施するのか、という判断は、実は簡単です。
目的変数がどんな種類のデータなのか、ということを考えればいいだけ。
- 目的変数が連続量：共分散分析（重回帰分析）
- 目的変数が2値データ（カテゴリカルデータ）：ロジスティック回帰
- 目的変数が生存時間データ：Cox比例ハザードモデル
ということなので、ロジスティック回帰分析を実施するには目的変数が二値のカテゴリカルデータであることが必要だと理解できました。
では早速、EZRでロジスティック回帰を実践していきましょう！
EZRで実際にロジスティック回帰を実施する方法
EZRでロジスティック回帰を実施します。
今回は自治医科大学さんが提供しているサンプルデータの中から「Eye」を使ってみます。
「Sex」「Grade」「NewFactor」「Disease」の4種類のデータがあります。
そのため、性別が共変量だったと仮定して、“性別という共変量の影響を取り除き、GradeごとにDiseaseのなり易さがどれぐらい変わるのか”ということをやります。
では実際にやっていきましょう！
EZRにロジスティック回帰分析をするためのデータを取り込む
ではここから、EZRにデータを取り込みます。
まずは、サンプルデータを適切な場所に保存しておきましょう。
EZRを開き、「ファイル」→「データのインポート」→「ファイルまたはクリップボード, URLからテキストデータを読み込む」を選択します。
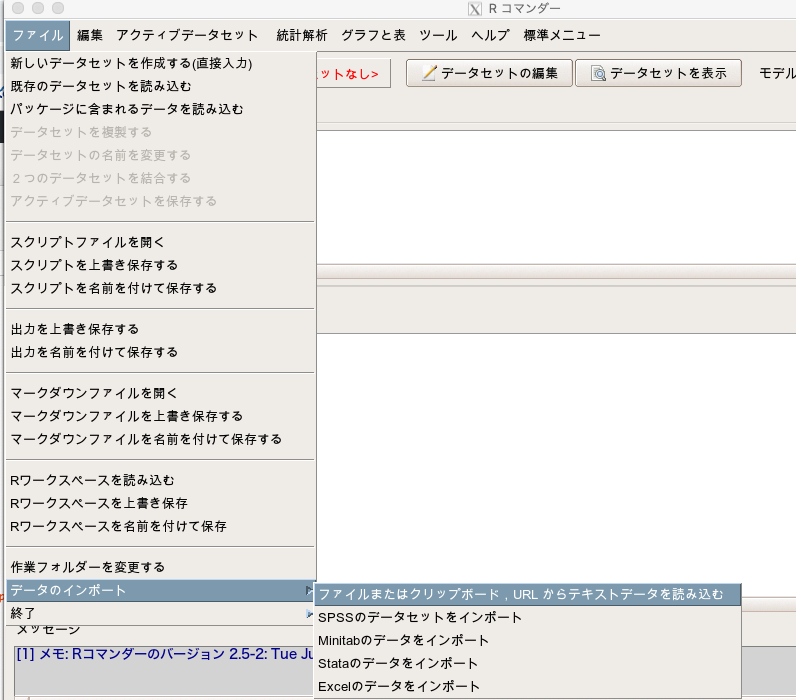
データセット名は「logistic」にしましょう（実際はなんでもよい）。
そして「ローカルファイルシステム」と「カンマ」にチェックを入れてOKを押します。
データセットが「logistic」になっていることを確認し、「表示」を押してデータが正しく表示されれば取り込み完了です。
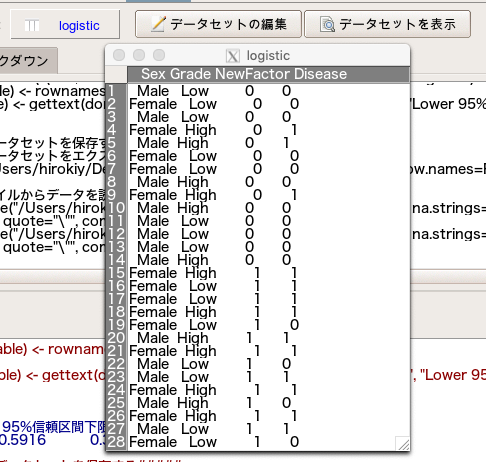
EZRでロジスティック回帰分析を実践する！
解析するための準備が整いましたので、早速、ロジスティック回帰を実施してみましょう。
ロジスティック回帰を実施するには、以下の手順で行います。
「統計解析」→「名義変数の解析」→「二値変数に対する多変量解析（ロジスティック回帰）」
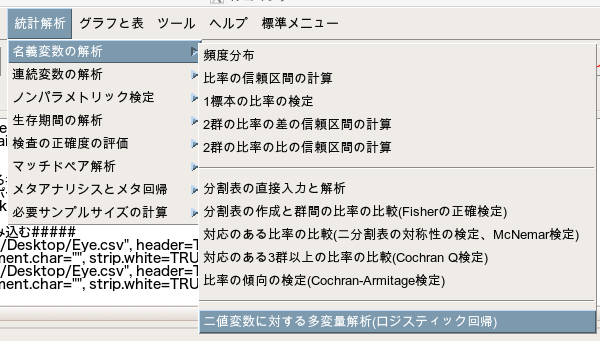
- 目的変数で「Disease」を選択します。（変数をダブルクリックすることで選択できます。）
- 説明変数に「Grade」と「Sex」を選択します。（こちらもダブルクリックです。）
他は、いじらなくてOKです。
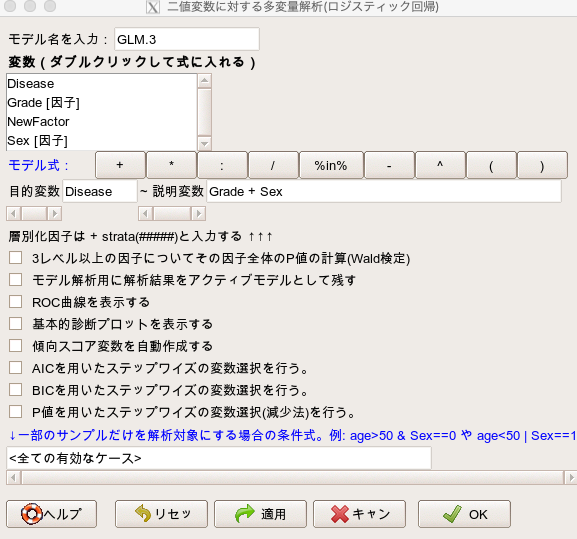
これで解析を実行すると、以下の解析を自動で行ってくれます。
- ロジスティック回帰分析を実施した結果の表の作成
- 多重共線性に関する確認
- オッズとその95%信頼区間に関する表の作成
EZRで実施したロジスティック回帰分析結果の解釈をしよう
実際にロジスティック回帰分析が実施できました。
では、結果の解釈をしていきましょう。
ロジスティック回帰分析の結果解釈
まずはロジスティック回帰分析を実施した結果の表の解析結果です。
かなりの情報量が詰まっていますね。
glm(formula = Disease ~ Grade + Sex, family = binomial(logit), data = logistic)
というのは、ざっくり言うと「ロジスティック回帰分析をしましたよ」ということ。
そして、その回帰式が“Disease=Grade+Sex”ということですね。
Residuals:には、残差に関する情報が載っています。
ここは特に解釈することはないので、スキップで。
重要なのが、Coeffifients:の部分です。
ここには、説明変数で入れた「Grade」と「Sex」の回帰係数の結果が記載されています。
ここの結果で重要なのが「Estimate」と「Pr(>|t|)」の二つ。
Estimateは、回帰係数の点推定値です。
Pr(>|t|)は、“回帰係数が0である”という帰無仮説に対する検定結果です。
つまりここのP値が0.05を下回った場合に、回帰係数は0ではなさそうだ、ということが言えます。
更に言い換えると、P値が0.05を下回った場合には“この説明変数は目的変数に対して影響を与えていそうだ”ということが言えます。
今回の結果でいうと、GradeはP=0.0326なので有意水準5%で有意差あり。
性別は有意差なし、です。
今回知りたかったことは、性別が共変量だったと仮定して、“性別という共変量の影響を取り除き、GradeごとにDiseaseのなり易さがどれぐらい変わるのか”ということです。
今回の結果から、Diseaseあり/なしに関して性別の影響を除いてGradeを比較したら、有意差はあった、という結論を導くことができます。
つまり、GradeごとにDiseaseのなり易さが違う、ということが言えます。
EZRでロジスティック回帰分析した結果出てきた多重共線性に関する表の解釈
その次に、多重共線性に関する表が出力されています。
多重共線性とは、説明変数として選択されている変数間の相関が高い場合に、ちゃんとした推定値を出力してくれない、という問題のことです。
EZRではvifという指標で多重共線性の問題を示しています。
vifの見方は、ざっくり言うと、以下の通りです。
- vifが5以上だと多重共線性が疑わしい
- vifが10以上だと多重共線性がかなり疑わしい
今回はvifが1なので全く問題ありません。
オッズ比に関する表の解釈
次に、各説明変数のオッズ比に関する結果が出力されています。
オッズ比の点推定値と95%信頼区間、そしてP値です。
オッズ比は1だった場合に「差がない」といえます。
そのため、1から遠ければ遠い点推定値であるほど、差があるということが言えます。
ここからも、有意水準が0.05だった時に有意差があるかどうかわかります。
Gradeは95%信頼区間が1を跨いでいないため、有意差あり。
Sexは95%信頼区間が1を跨いでいるため、有意差なし。
この95%信頼区間と有意差の関係は、一目見て理解できるようになっていたいですね。
EZRでロジスティック回帰分析に関して単変量解析するとどうなるの？
今回も共分散分析と同様に説明変数を2つ含め、共変量の影響を除いて群間比較しました。
今回のデータでは、Sexを共変量としていましたよね。
では、共変量がなかった時に本当に結果が変わるのか！？ということをやってみましょう。
やり方の手順は先ほどと同じで、説明変数にはGradeの１つだけ入れます。
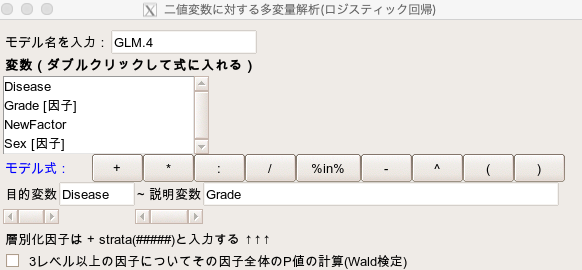
すると、下記のような結果が出力されています。
Sexで調整した場合にはP=0.0326でしたが、Sexで調整しないとP=0.0296という結果が出ました。
P値がそれほど変動していないため、Sexによる調整の有無が、Gradeの結果にそれほど影響を与えていなかったことが分かります。
EZRで多変量ロジスティック回帰分析の適合度検定（Hosmer-Lemeshow検定）を実施する方法
ロジスティック回帰分析をすると、そのモデルの適合度を知りたい時があります。
ロジスティック回帰分析での適合度検定としてはHosmer-Lemeshow検定が有名なのですが、EZRのデフォルト機能ではHosmer-Lemeshow検定結果が出力されません。
ではどうすればいいのかと言うと、EZR上でRのプログラムを実行すればOK。
実はやり方としても簡単なんです。
まず、Hosmer-Lemeshow検定を実施することができるRのパッケージをインストールします。
そのパッケージは「ResourceSelection」というもの。
以下のように、すればパッケージをインストールできます。
- パッケージとデータ＞パッケージインストーラをクリック
- ResourceSelectionを検索
- 「一覧を取得」をクリック
- 「依存パッケージも含める」にチェックを入れ、「選択をインストール」をクリック
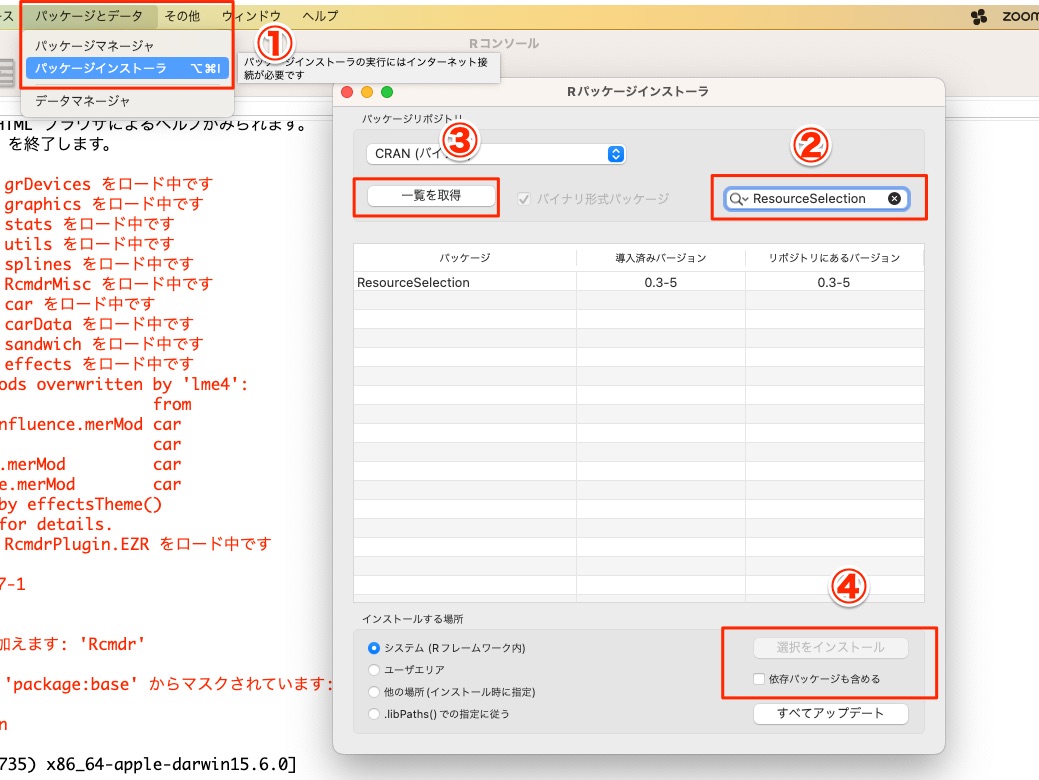
ただ、パソコンの環境によってはこの手順ではインストールできないかもしれないので「R パッケージインストール方法」などで検索して調べてみてください。
パッケージがインストールできたら、ロジスティック回帰分析を実行します。
すでにロジスティック回帰分析を実施済みであれば、この手順はスキップで問題ないです。
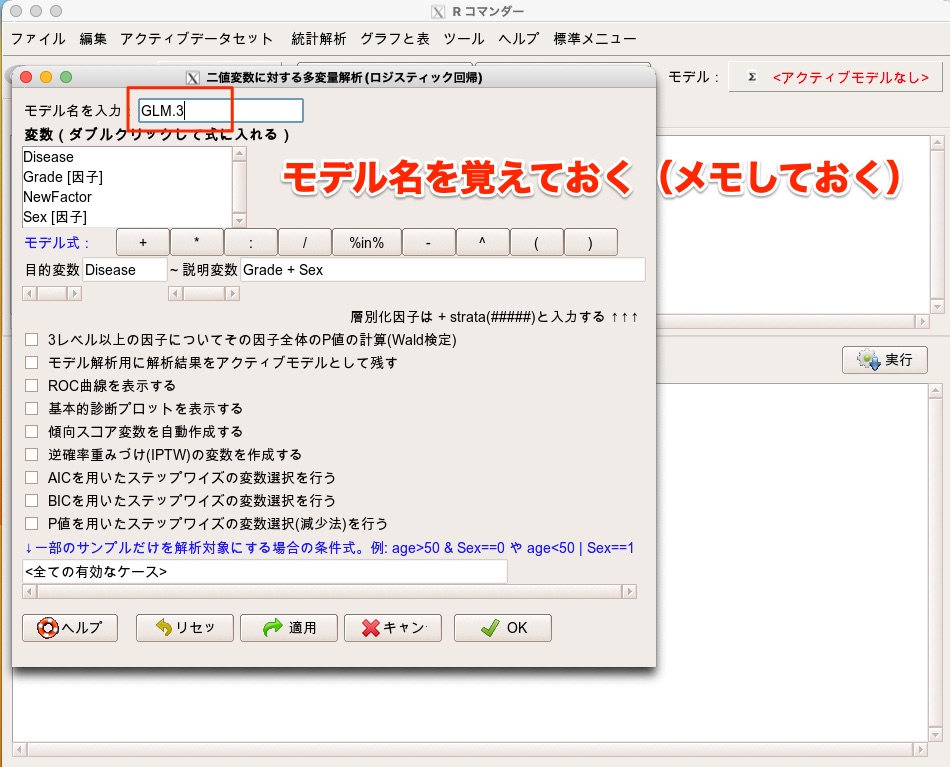
一点だけ注意なのは、ロジスティック回帰分析をした時のモデル名を覚えておくこと。
このモデル名はHosmer-Lemeshow検定を実施する際に必要になります。
ロジスティック回帰分析を実施した後は、以下の2行をRスクリプト部分に追加し、この2行を選択して「実行」を押します。
library(ResourceSelection)
hoslem.test(GLM.3$y, GLM.3$fitted.values)
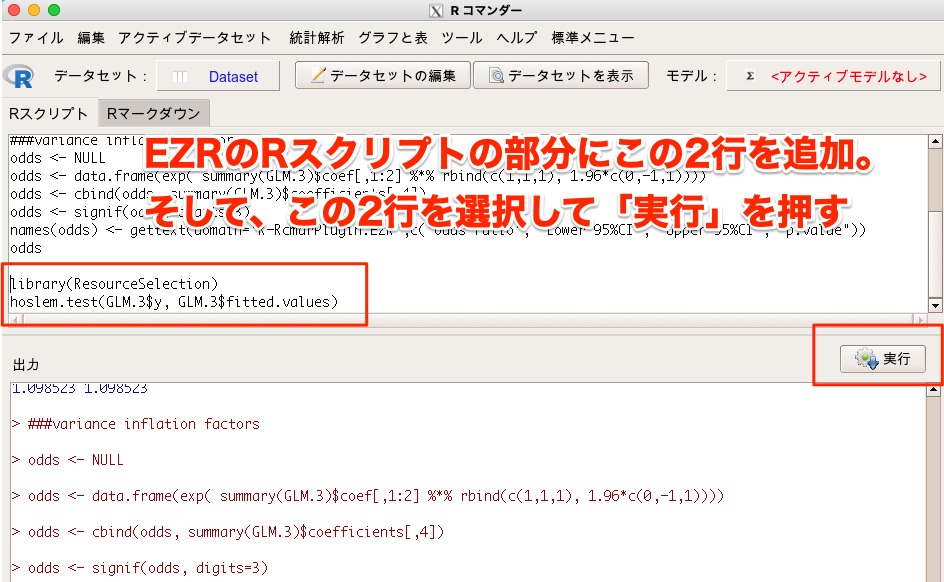
2行目の「GLM.3」となっている部分は、ロジスティック回帰分析を実施した時のモデルの名前を入力してください。
この2行を実施すると、Hosmer-Lemeshowの適合度検定（Goodness of fit (GOF)）が実施されます。
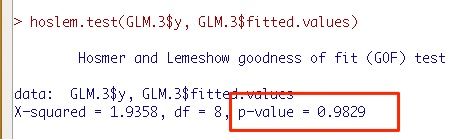
結果の見方としては「有意差がなければ（p値が0.05より大きければ）適合しているとみなす」という使い方です。
ただし、p値はサンプルサイズに依存する指標のため、絶対的な基準ではないことに注意してください。
動画でもHosmer-Lemeshow検定の実施方法はお伝えしているので、併せてご確認ください。
まとめ
今回は、EZRで多変量解析の一つであるロジスティック回帰分析を実施しました。
ロジスティック回帰分析は、応答変数（目的変数）が二値のカテゴリカルデータの際に使用できる解析手法です。
これを実践し、結果の解釈をすることができれば、必ず実務で役に立ちます。
第1章：医学論文の書き方。絶対にやってはいけないことと絶対にやった方がいいこと
第2章：先行研究をレビューし、研究の計画を立てる
第3章：どんな研究をするか決める
第4章：研究ではどんなデータを取得すればいいの？
第5章：取得したデータに最適な解析手法の決め方
第6章：実際に統計解析ソフトで解析する方法
第7章：解析の結果を解釈する
もしあなたがこれまでに、何とか統計をマスターしようと散々苦労し、何冊もの統計の本を読み、セミナーに参加してみたのに、それでも統計が苦手なら…
私からプレゼントする内容は、あなたがずっと待ちわびていたものです。
[…] 例えばロジスティック回帰分析でどんな変数を組み合わせるのが1番いいのか、というモデル選択（変数選択）を実施しますよね。 […]