正規分布をエクセルでグラフ化！ガウス分布の図を乱数を使って作成する

正規分布は、統計を学ぶ上で絶対に把握しなければならない分布です。

正規分布とは、平均値と標準偏差が決まれば、1つに決まる分布。

 

このページでは、エクセルを使って正規分布のグラフを描いてみます。

実際に、乱数を使った正規分布の作り方は3ステップです！

このページを見れば、あなたも乱数を用いて、自由自在にエクセルで正規分布を作ることができるようになります！

 

正規分布（ガウス分布）とは？

正規分布はガウス分布とも呼ばれ、以下の式で与えられる分布です。

式は覚えなくて良いですよ！

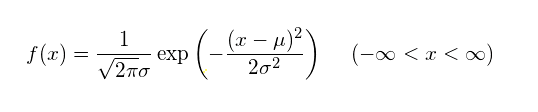
この正規分布の式で注目して欲しいのが、μ（ミューと読みます）とσ（シグマと読みます）の２つの記号です。

これはそれぞれ、μ＝平均、σ＝標準偏差、を表しています。

で、なぜこの２つの記号に注目したか。

それは、「μ＝平均、σ＝標準偏差の２つさえ決まれば、正規分布の形が決まる」という性質を持つからです。

これは重要なので、絶対覚えてくださいね！

重要なので、もう一度書いておきます。

 

 

この正規分布は、統計の中でかなり重要な分布です。

というのも、95%信頼区間を正確に理解するためにも、正規分布の知識が必須だからです。

統計検定2級の問題も、正規分布の性質を知らなければ解くことができない問題が毎年出ていますね！

 

正規分布（ガウス分布）をエクセルでグラフを描く！

このページでは、このようなグラフを描くことをゴールにします。

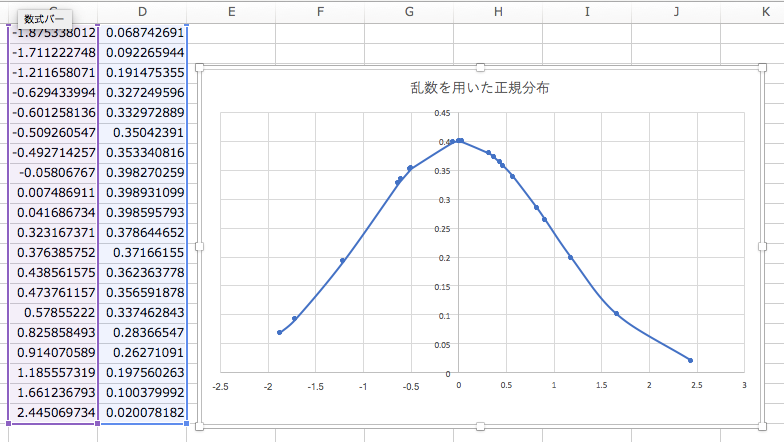
たったの３ステップで出来てしまいます！

 

正規分布をエクセルで描く方法ステップ１：乱数を発生させる

まずは最初のステップです。

最初は乱数を使って、正規分布のデータを発生させます。

今回は、μ＝平均＝０、σ＝標準偏差＝１の正規分布を作成します。

 

以下の関数を用いて、乱数を発生させます。

RAND()の部分が、乱数を発生させている部分になります。

で、平均が０、標準偏差が１を入力しています。

「μ＝平均、σ＝標準偏差の２つさえ決まれば、正規分布の形が決まる」ため、エクセルでも平均と標準偏差の2つを指定する必要がありますね。

 

 

 

上記の関数で1つのデータが発生します。

A1に=NORM.INV(RAND(),0,1)と入っていますね。

 

それを、今回は20個のデータを発生させます。

そのため、A１の関数をコピペして20個データを発生させましょう。

 

RAND()はセルによって常に値が変わります。

そのため、何も考えずにコピペすることで異なる20個のデータが作成できます。

 

これで、20個の乱数を用いたデータを作成できました。

ですが、ちょっとこれでは使いづらいです。

というのも、RAND()は、何か操作するたびに値が変わってしまうから。

 

例えば、他のセルに値を入れてエンターを押してみましょう。

そうすると、RAND()が入っている部分のデータが一斉に変わります。

すると、データの再現性が取れないので、少々使いづらいですね。

そのため、A列をコピーして別の列（ここではC列）に「値のペースト」をします。

そうすることで、何か操作するたびに値が変わるということがなくなります。

 

 

で、データの完成形がこれです。

 

正規分布をエクセルで描く方法ステップ２：乱数に応じた、正規分布の確率を算出する

次のステップです。

ステップ１で作成したデータに応じて、正規分布の確率を算出してあげます。

隣の列に、このような関数を入れます。

 

上記の関数で、C１と入力している部分は、「値のペーストをしたセル」を入れてくださいね。

で、最後の関数形式は、FALSEを入れます。

 

関数形式がTRUEだと、累積確率を出してしまうからです。

累積確率に関しては、また別のところで解説しますね。

 

とりあえずこのページでは、「FALSEにする」ということだけ覚えてください。

この関数を、また20個ほどコピペします。

すると、以下のようにD列にも20個のデータが作成されました。

 

正規分布をエクセルで描く方法ステップ３：グラフを描く

これでデータの準備はできました。

次は、今まで作成したデータを元にしてグラフを描くだけです。

 

ですが、グラフ化の前に、もう一つだけ作業を。

それは、X軸となるデータを小さい順に並べておく、ということです。

今回のX軸となるデータは、C列です。

なので、C列とD列の各２０個のデータを選択肢、C列をキーにして小さい順に並べます。

 

 

これでやっと、すべての準備が完了です。

「挿入」タブから、散布図（平滑線とマーカー）を選びます。

これは、隣の散布図（平滑線）を選んでも大丈夫です。

マーカーとは、データの点のことを示しているため、点があるかないかだけの違いなので。

お好みでどうぞ。

 

 

そうすると、冒頭のグラフができました。

全然難しくないですね！

 

ちなみに、これだとガタガタしたグラフです。

なんとなく、滑らかなグラフを描いてみたい、という思いもありますよね？

であれば、データを増やせばOKです。

 

この例では、20個のデータでグラフを書きました。

しかし、これを200個のデータで作成すると、以下のような、滑らかなグラフになります。

 

 

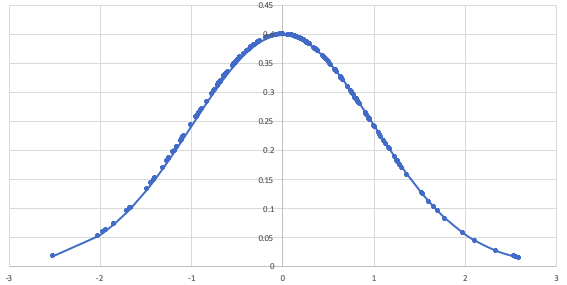
かなり滑らかですよね！！

 

 

正規分布をエクセルで描く方法まとめ

このページで、乱数を使って正規分布のグラフを描いてみることを実践しました。

正規分布は、統計を学ぶ上で、絶対に欠かすことのできない分布です。

ぜひ、一度自分でグラフを作ってみて、理解を深めることをお勧めしますよ！

たったの３ステップで簡単にできますので！

 

＞＞正規分布に必要な知識：歪度と尖度とは？

＞＞正規性の検定は必要なのか？