医薬統計で扱うデータの種類は多岐にわたり、そのデータの特性によって統計解析手法や検定手法が異なります。
逆に言えば、データの種類が決まれば自ずと解析手法も変わるということ。
主なデータの種類は、量的データ(連続尺度)、質的データ(名義尺度)、生存時間データなどがあります。
この記事では、各データがどのような特性を持っているかを理解し、データの種類に応じてどのような統計解析手法が適用されるかを学びましょう。
質的データや量的データとは?具体例を用いてわかりやすく解説!

医薬統計において、扱うことが多いデータは大きく分けて3種類です。
- 量的データ(連続尺度、連続データ)
- 質的データ(名義尺度、カテゴリカルデータ)
- 生存時間データ
量的データや質的データは、医薬統計じゃなくても扱うことが多いです。
生存時間データに関しては、医薬統計で独特のデータかな、と思います。
次の章から、それぞれのデータがどのような特徴を持っており、それに応じてどのような統計学的な検定手法が採用されるのか、理解していきましょう。
データの種類1:量的データ(連続尺度、連続データ)とは?その統計解析手法
世の中で最もありふれているデータが量的データ(連続尺度)です。
量的データとは、身長や体重のように、精度の高い測定法によればいくらでも正確な値が得られるデータのことです。
実際は離散量であるが連続量として取り扱ってもかまわないようなものもあります。
例えば、試験の点数などは一般的に、90点や91点という値を取りますが、90.2点や90.8点という点数は取りません。
ですが、そのような場合であっても連続データとして取り扱うと都合が良い場合が多いため、連続データとして扱います。
連続データのもう一つの特徴としては、データ上のどこであってもその間隔が同じ意味を持つ、ということです。
例えば身長であれば、150cmと155cmの間の5cmと、190cmと195cmの間の5cmは同じ意味を持ちます。
試験結果も、10点と30点の間の20点と、80点から100点の間の20点では、同じ意味を持ちます。
「データ上のどこであってもその間隔が同じ意味を持つ」という特徴は、当たり前のようなことではありますが、実はカテゴリカルデータとの違いを認識するために重要な特徴でもあります。
このような量的データに対しては、平均値や分散などの要約統計量を算出するのが望ましいですね。
以下のような表を作成できれば、完璧です。
| 男性 | 女性 | |
| 平均値(SD) | XXX(XX) | YYY(YY) |
| 中央値 | XXX | YYY |
| 範囲 | XXX-XXX | YYY-YYY |
| 四分位範囲 | XXX-XXX | YYY-YYY |
| 95%信頼区間 | XXX-XXX | YYY-YYY |
また、グラフとしてはヒストグラムで正規分布に従っているかどうかを確認したり、箱ひげ図で中央値や四分位範囲を確認することがとても良いアプローチです。
そして、統計学的検定としては、パラメトリック検定ならT検定を、ノンパラメトリック検定であればウィルコクソン検定を実施することが良いです。
データの種類2:質的データ(名義尺度、カテゴリカルデータ)とは?分割表作成が重要
次は、質的データ(名義尺度、カテゴリカルデータ)についてです。
カテゴリカルデータと聞いて、あなたはどのようなデータか想像できますか?
カテゴリカルデータの一例としては、性別が挙げられます。
男性というカテゴリと、女性というカテゴリに分けられますね。
性別のように数値化できないデータ、または、数値化したとしてもその数字の間隔に意味がないもののデータのことを、カテゴリカルデータと呼びます。
例えば商品アンケートで「この商品の感想を教えてください」という設問に対し「良い、普通、悪い」という3つから選ぶとします。
その設問のアンケートデータを「3点、2点、1点」というように、点数化することもできますね。
ですが、この3点と2点の間の1点、もしくは2点と1点の間の1点に関して、同じ1点ですがその間隔は同じ意味を持つとは限りません。
そのような場合、やはりカテゴリカルデータとして扱うほうが適切です。
カテゴリカルデータの要約方法は簡単です。
数と割合の二つを出力すれば、基本的には問題ありません。
さらには、これらを表形式でまとめることをお勧めします。
分割表と呼ばれる表を作ることが、カテゴリカルデータの要約方法としては適切です。
分割表の例としては、100人の男女に右利きか左利きかを聞いてみた結果の表が以下になります。
| 男性 | 女性 | 合計 | |
| 右利き | 43 | 44 | 87 |
| 左利き | 9 | 4 | 13 |
| 合計 | 52 | 48 | 100 |
分割表から読み取れることはとても多いのですが、その詳細は別ページで解説していますので、そちらをご参照ください。
そして、カテゴリカルデータの統計学的な検定手法です。
2つあります。
- フィッシャーの正確確率検定
- カイ二乗検定
この2つさえ理解しておけば、全く問題ありません。
2つの検定の使い分けですが、分割表で5未満のセルがあれば、その時にはフィッシャーの正確確率検定を実施することが良いです。
それ以外の場合には、カイ二乗検定を実施することで問題ありません。
ただ、理解の仕方としては「サンプルサイズが小さい時にカイ二乗検定はNG。サンプルサイズが小さくても大きくてもフィッシャーの正確確率検定はいつでも使ってOK」という理解をしていただければと思います。
多変量解析としては、ロジスティック回帰分析を使うことになります。
データの種類3:生存時間データ
医薬統計では、生存時間データというものを扱うことがあります。
がん領域を知っている方であれば恐らく知っているデータの種類だと思いますが、それ以外の方はあまりなじみがないかもしれません。
生存時間データを解析する統計手法を、生存時間解析、と呼びます。
生存時間解析を一言でいうと、その名の通り「時間」を解析する方法です。
時間は、「1時間」とか「75日」とか、連続データとして扱って解析しても良さそうです。
連続データとして扱えば、T検定やウィルコクソンの順位和検定を使えばいいですよね。
ではなぜわざわざ生存時間解析、というものを使うのでしょうか。
詳しくは生存時間解析の基礎のページで解説していますが、「イベント」と「打ち切り」という概念があるため、連続データとして扱うと不都合が出てきます。
そのため、生存時間解析という、また別の枠組みで解析する必要があるのです。
生存時間解析でのグラフとして有名なのが、カプランマイヤー曲線ですね。
カプランマイヤー曲線では、中央値やX年生存率が一目でわかる、かなり有用なグラフです。
下記のグラフが、カプランマイヤー曲線の一例です。
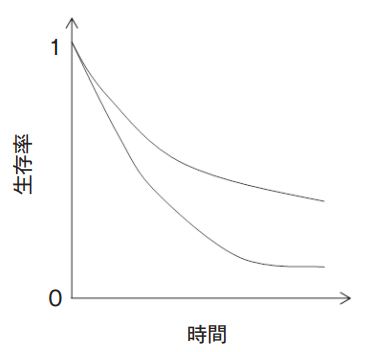
そして、検定としてはログランク検定と一般化ウィルコクソン検定が有名です。
多変量解析としてはCox比例ハザードモデルですよね。
「カプランマイヤー曲線」「ログランク検定」「一般化ウィルコクソン検定」「Cox比例ハザードモデル」の4つを理解していれば、最低限の生存時間解析は可能です。
データの種類4:カウントデータ
これはあまりなじみがないかもしれません。
生存時間データの目的の反応は、観測対象となる個体に、一度だけ起きる事象だとしました。
しかし、データによっては、複数回起きる事象があります。
例えば、血友病という病気は血が固まりにくく出血が起こりやすい病気です。
出血というのはその人に一度だけ起きるとは限らず、1年間に10回など、複数回起こりえますね。
そのような場合に、出血回数をカウントデータと呼ぶことがあります。
もちろん連続データとして扱うことも可能なのですが、カウントデータの性質として「観察期間に応じて回数は増える」という性質があります。
そのため、観察した期間を考慮して解析をしなければなりません。
また、このデータは、もし「初めての出血までの時間」というものに興味があるとき、生存時間データとして扱う必要があります。
質的データや量的データに関するまとめ

医薬統計を実施する上で、重要な「量的データ」「質的データ」「生存時間データ」「カウントデータ」の3種類(+1種類)のデータを紹介しました。
これらの扱い方がわかれば、医薬統計としてはほぼ網羅できますので、是非とも理解しましょう!









コメント
コメント一覧 (14件)
[…] 一番優しい、医薬品開発に必要な統計学の教本 データの種類 […]
[…] >>データの種類に応じて解析方法は決まる […]
[…] カイ二乗検定が分割表を検定する方法ということは、2種類のカテゴリカルデータが必要になります。 […]
[…] 統計解析をする前に”疾患の有無”や”自宅退院か転院か”といった2値のカテゴリカルデータなどをダミー変数に変換する必要がある場合はしばしばあります。 […]
[…] カテゴリカル変数とは、いわゆる質的データですね。 […]
[…] カッパ係数とは、質的データ(カテゴリカルデータ)に対して2つの検査結果の一致度合いを評価する指標のことです。 […]
[…] 連続データやカテゴリカルデータなどは比較的身近なデータですが、カウントデータはどんなデータでしょうか? […]
[…] 「68週の体重の変化率」は連続量(量的データ)であり、「68週の体重がベースラインに比べて5%以上減少したか否か」は2値のカテゴリカル変数(質的データ)ですね。 […]
[…] 例数に関しては上述の通り、「その有害事象を発現したかどうかの有無」を数えているため、データとしては2値のカテゴリカルデータになります。 […]
[…] いわゆる量的データ(連続量)に対する「要約統計量」を算出する際には算術平均値が用いられます。 […]
[…] 例えば、年齢、体重などの連続変数(量的データ)の場合には、T検定(正規分布の場合)やマンホイットニーのU検定(正規分布じゃない場合)が使われます。 […]
[…] まずは、EZRでアウトカムが2値のカテゴリカルデータである場合のメタアナリシスを実施していきましょう。 […]
[…] 連続量(量的データ)をアウトカム(目的変数)にする場合、背景情報での交絡バイアスを小さくしたいと考えた時、共分散分析の実施が候補に挙げられます。 […]
[…] Clopper-Pearsonの信頼区間は、2値のカテゴリカルデータの割合に関して95%信頼区間を算出したい、というときに選択肢として入ってくる信頼区間です。 […]