標準誤差とは？標準偏差との違いをわかりやすく！計算式やエラーバーでの使い分けは？

統計学は、バラツキ（誤差）を扱うことに、ユニークな点があります。

データにバラツキがなければ、統計を使う必要なんてありません。

それぐらい、統計ではバラツキが重要。

しかしバラツキといっても、似たような用語の指標として「標準偏差」と「標準誤差」の二種類があります。

標準偏差と標準誤差は何が違うのでしょうか。

標準偏差と標準誤差のどちらをつければいいのでしょうか。

標準偏差と標準誤差は似ているようで実は全く異なる概念です。

この記事では、標準偏差と標準誤差の違いを明確にし、どのような時に標準偏差を使うべきで、どのような時に標準誤差を使うべきかを明らかにしていきます。

標準偏差（SD）と標準誤差（SE）の違いは？エラーバーでの使い分けは？

結論から言えば、標準偏差と標準誤差は下記のような違いがあります。

• 標準偏差は、データのバラツキを表すパラメーターです。
• 標準誤差は、推定量のバラツキ（=精度、信頼性）を表します。

標準偏差はSD：Standard deviation、標準誤差はSE：Standard Error

と英語で書かれることもあります。

では、標準偏差と標準誤差にはどのような違いがあるのでしょうか。

例えば実験データから棒グラフを作成するとき、下記のようなエラーバーをつけますよね。

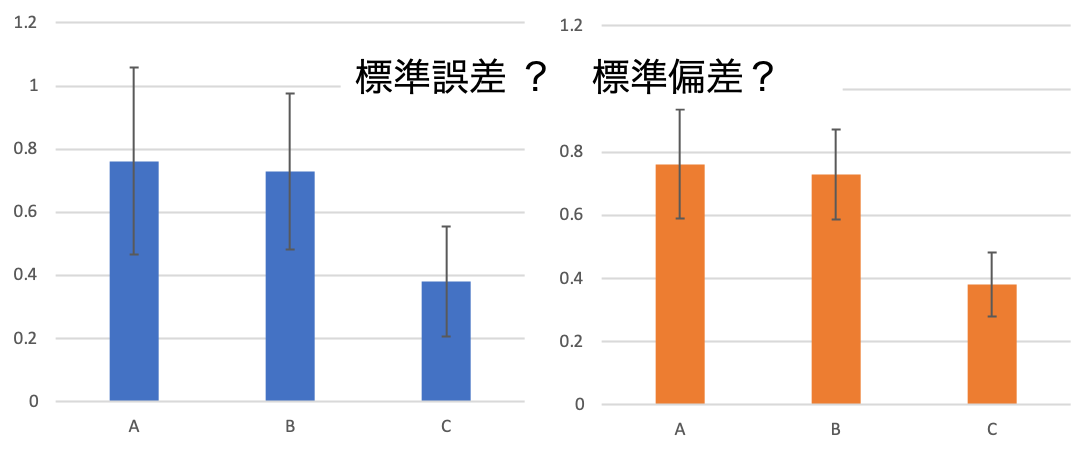
この時、標準偏差にすべき？

それとも標準誤差にすべき？

というのが疑問になると思います。

標準偏差とは？わかりやすく言うとどんなこと？

“標準偏差”は一言で言うならば、データのバラツキを表すパラメーターです。

もうちょっと具体的にすると、データが平均値からどれくらい散らばっているかを示す指標。

そのため、標準偏差には次のような特徴があります。

• 標準偏差が小さい　→ 平均に近いデータが多い　→データのバラツキが小さい
• 標準偏差が大きい　→ 平均から離れたデータが多い　→データのバラツキが大きい

詳しくは、正規分布とは？簡単にわかりやすく標準偏差との関係やエクセルでのグラフ化を解説の記事で紹介しています。

標準誤差とは？わかりやすく言うとどんなこと？

標準誤差は“推定量の標準偏差”です。

つまり、標準誤差は推定量のバラツキ（=精度）を表します。

母集団と標本の関係には、

“母集団の性質と、母集団から抽出した標本の性質は一緒ではない”という性質があります。

そのため、標本から母集団の性質を推定する必要があるのです。

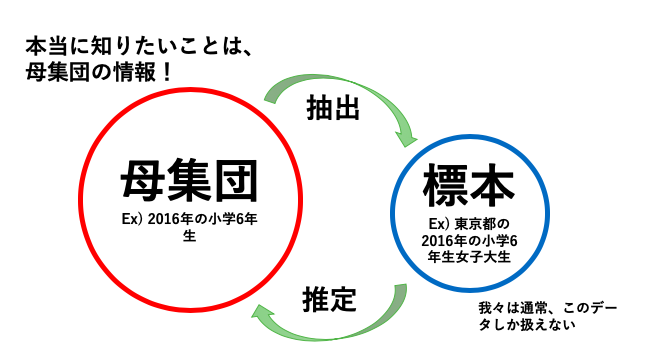
そして、標本から母集団の性質を推定した統計量のことを、推定量と言います。

母集団と標本の関係はこちらにも記していますので参照してみてください。

>>>不偏分散とは？簡単にわかりやすくn-1で割る理由とエクセルの関数を解説！

推定量は、あくまで標本からの推定した統計量でしかありません。

そのため、実際の母集団の統計量とは多少の誤差を含みます。

この推定量と母集団の統計量の誤差を、推定量の標準偏差として表すものを標準誤差と言います。

つまり、標準誤差は推定量のバラツキ（=精度）を表しています。

• 標準誤差が小さいことは、推定量の精度が良いことを意味します。
• 標準誤差が大きいことは、推定量の精度が悪いことを意味します。

標本平均の誤差範囲としての標準誤差

標準誤差は、推定量の標準偏差を表しますが、一般的に標準誤差は標本平均の誤差範囲を表します。

冒頭で述べた、グラフで使うエラーバーとしての標準誤差も標本平均の誤差範囲を意味します！

標準誤差は次の式で表すことができます。

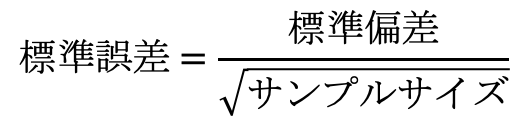
ここで、サンプルサイズは標本のデータの数を表しています。

このような式になるのは、“母集団の分布にかかわらず、母集団から抽出された標本の数が十分に多い場合、標本平均の分布は正規分布に従う”といった性質が存在するからです。

>>>正規分布とは？簡単にわかりやすく標準偏差との関係やエクセルでのグラフ化を解説

この性質で出現する正規分布での標準偏差は、“標準偏差/√サンプルサイズ”になります。

だから平均の標準偏差は上の式で表します。

標準誤差も、”標本平均の標準偏差”ですので、標準偏差としての性質を持ちます。

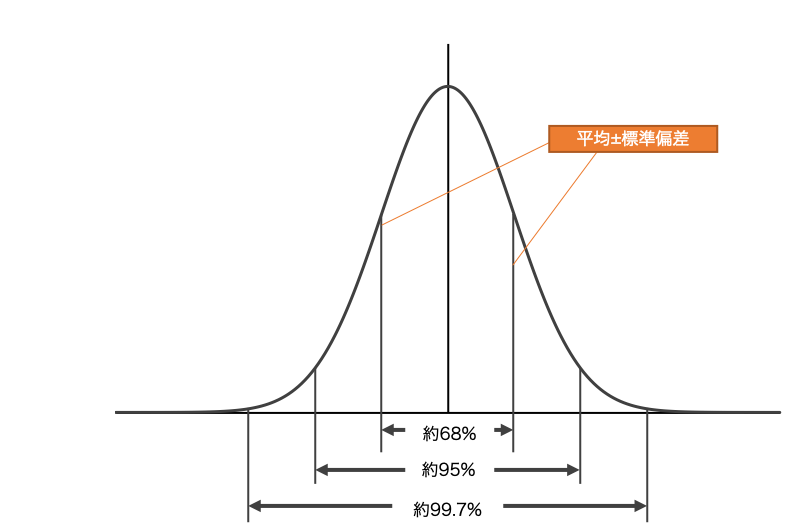
これはつまり、

• 標本平均±標準誤差の範囲中に約68パーセントの確率で母平均が含まれる。
• 標本平均±2×標準誤差の範囲中に約95パーセントの確率で母平均が含まれる。
• 標本平均±3×標準誤差の範囲中に約99.7パーセントの確率で母平均が含まれる。

という性質があるということです。

そのため、標準偏差を求めると、母平均が存在する区間の推定ができます。

標準偏差の性質については、

>>>正規分布とは？簡単にわかりやすく標準偏差との関係やエクセルでのグラフ化を解説

で解説しています。

また、95%信頼区間も、標準誤差の上記の性質を使って理解することができます。

標準偏差と標準誤差の使い分けは？

標準偏差はデータの散らばり具合を、標準誤差はサンプル平均の信頼性を示します。

そのため、標準偏差はデータそのものの特性を、標準誤差はサンプルを通して母集団についての情報を得るための指標です。

• データのバラツキが知りたいとき：標準偏差
• 母集団の性質を知りたいときは：　標準誤差

特に、母平均を推定したいときに、標準誤差を用います。

目的が異なりますので、ぜひ上記のことは強烈に意識していただければと思います！

標準偏差を使うとき

標準偏差がわかれば、その範囲にどれくらいの観測データが含まれているかが分かります。

そのため、

• データのバラツキを示したいとき
• データのバラツキを比べたいとき

標準偏差を使うべきです。

例えば医学論文で言えば、被験者背景データ（Table1）は標準偏差で示すべきです。

そうすることで、どのような特徴を持った集団が、この論文の対象なのかを読者は知ることができるからです。

標準誤差を使うとき

アンケートなどを行うとき、

どのサイズのサンプルサイズが必要かを考えるときも

標準誤差を利用します。

ここでは一例として、内閣支持率の世論調査を考えてみたとします。

2019年時点で日本国内に有権者数は約1億人います。（総務省統計による）

何人くらいからアンケートをとると、どれくらいの精度で支持率が確認できるでしょうか。

ここではアンケートの結果、内閣支持率は50%だったと過程します。

（注意：ここでは二項分布を用いています。）

二項分布の標準誤差は

標準誤差=√確率×(1−確率)/サンプル数

で表します。

100人に聞いてみたとき

標準誤差=√0.5×(1−0.5)/100=0.05=5%

つまり、45~55%の間に約68パーセントの確率で有権者全員の支持率母平均が含まれます。

1000人に聞いてみたとき

標準誤差=√0.5×(1−0.5)/1000=0.0158=約1.6%

つまり、48.4~51.6%の間に約68パーセントの確率で有権者全員の支持率母平均が含まれます。

10000人に聞いてみたとき

標準誤差=√0.5×(1−0.5)/1000=0.005=約0.5%

つまり、49.5~50.5%の間に約68パーセントの確率で有権者全員の支持率母平均が含まれます。

このように、標準誤差を使えば、目的の精度に合わせて、サンプルサイズを決定することができます。

サンプルサイズに関して、より詳細に知りたい方はこちらをご覧ください。

＞＞サンプルサイズの決め方は？

Rで標準偏差と標準誤差を算出してみる！標準誤差の求め方も紹介！

実際に、サンプルデータを用いて標準偏差と標準誤差を出力してみます。

Rをダウンロードした際に含まれている「CO2」というデータを使います。標準誤差（Standard Error, SE）は下記の式で表されます。

$$SE = \frac{SD}{\sqrt{n}}$$

SDは標準偏差、nはサンプルサイズです。こちらの式を用いてプログラムを作成します。

#1度だけ実施する。過去にインストールしたことがあれば実行しなくてOK
install.packages("dplyr")


# dplyr パッケージを読み込む
library(dplyr)

# CO2データセットを使って、uptakeの要約統計量を計算
summary_stats <- CO2 %>%
  summarise(
    n = n(),
    mean = mean(uptake, na.rm = TRUE),
    sd = sd(uptake, na.rm = TRUE),
    median = median(uptake, na.rm = TRUE),
    min = min(uptake, na.rm = TRUE),
    max = max(uptake, na.rm = TRUE)
  )

# 計算結果の表示
print(summary_stats)

上記を実施すると、下記のような結果になりました。

n	84
Mean	27.2
SD	10.8
SE	1.18

標準偏差と標準誤差の違いに関してまとめ

• 標準偏差は、データのバラツキを表すパラメーター
• 標準誤差は、推定量のバラツキ（=精度）を表す
• データのバラツキが知りたいときは、標準偏差を用いる
• 母集団の性質を知りたいときは、標準誤差を用いる
• 標準誤差を使えば、目的の精度となるサンプルサイズを決定できる