GraphPad Prism は、簡単きれいに論文掲載可能なグラフを作成できるグラフ作成ソフトです!
しかも、検定が実行できて、有意差を示す「*」印を、グラフにすばやく書き入れることができます!
ここでは、分散分析のノンパラメトリック版である、Kruskal-Wallis(クラスカル・ウォリス)検定、Friedman(フリードマン)検定の実行例をご紹介します!
GraphPad Prism で Kruskal-Wallis 検定を実施してグラフを書く方法
Kruskal-Wallis 検定のためのデータ準備
Kruskal-Wallis 検定のためのデータは、カラムプロットと呼ばれる形式で入力します。
入力の仕方は、ダネット検定 Dunnett’s test のときと同じなので、参考にしてください。
以下のようにデータを入力します。
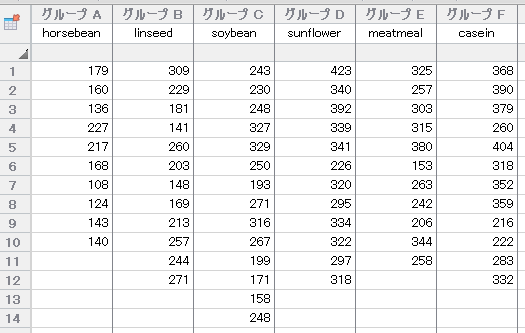
Kruskal-Wallis 検定の実施
次に左端のカラムから、「新しい分析」をクリックします。
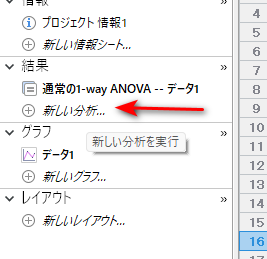
「データ分析」窓が開いたら、「カラム分析」の「1-way ANOVA(及び、ノンパラメトリック、・・・」が選択されているのを確認して、OK をクリックします。
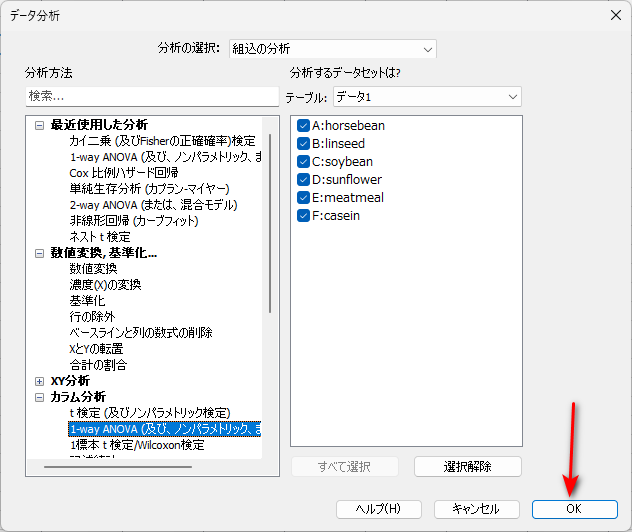
すでに一回分析している場合は、以下のダイアログが開きますので、再度分析のほうが選択されているのを確認して、OK をクリックします。
「パラメータ」窓が開いて、検定の設定をしていきます。
まず、「実験意図」タブで、「マッチング、対応なし」を選択し、「いいえ、ノンパラメトリック検定を行う」を選択します。
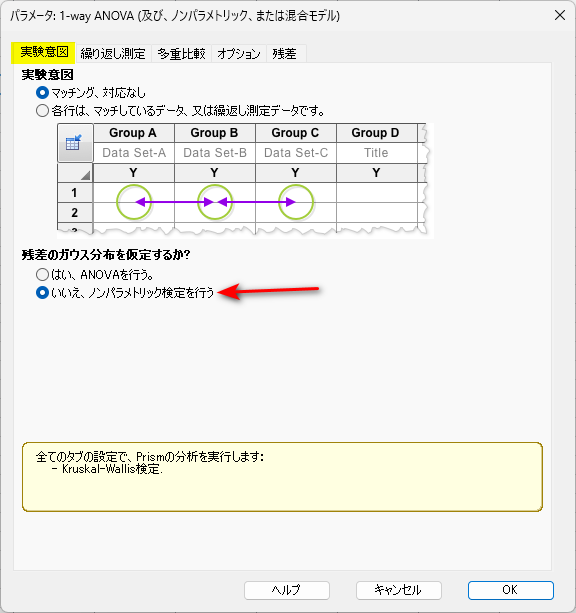
「繰り返し測定」タブは、何も選択しません。

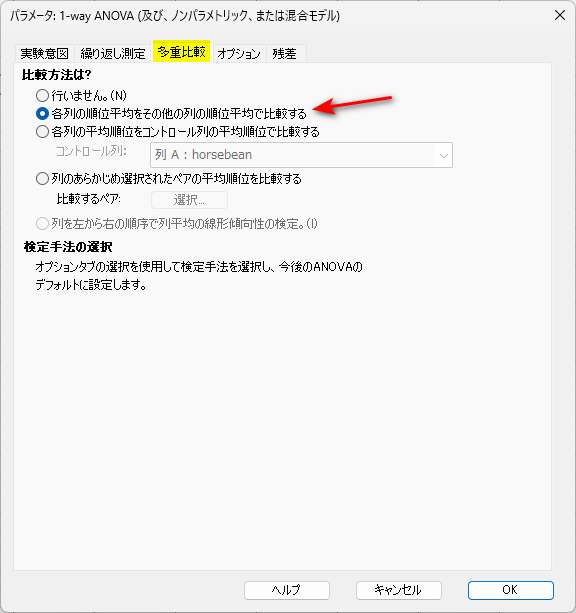
「多重比較」タブでは、「各列の順位平均をその他の列の順位平均で比較する」を選択します。
そうすると、多重比較も同時にできます。
「オプション」タブでは、多重比較検定を「多重比較の修正:統計的な仮説検定を使用(推奨)検定:Dunn」を選択します。
Dunn 検定の文献情報は、こちらです。
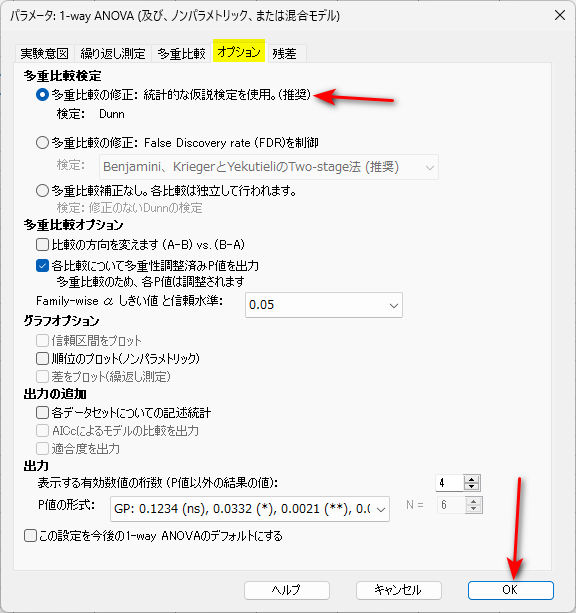
最後に、OK をクリックすると、検定が実行されます。
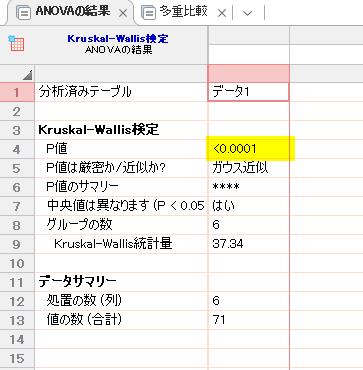
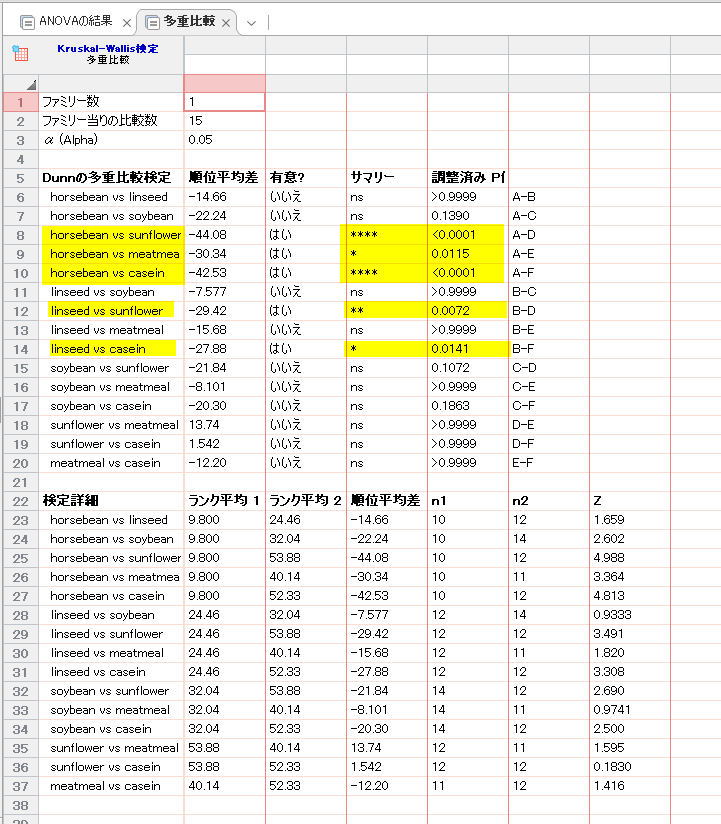
「ANOVA の結果」タブが、Kruskal-Wallis 検定の結果が表示されているタブです。
P 値が、<0.0001 で、統計学的有意であり、いずれかの群が異なると言えます。
多重比較は、Dunn 検定の結果です。
黄色ハイライトが統計学的有意に異なる群間です。
調整済み P 値は、そのまま有意水準(0.05)と比較すれば、有意かどうか判断できるようになっています。
グラフの書き方と検定結果の書き入れ方
では、今回の 6 グループのデータをグラフにして、検定結果を書き入れてみましょう。
左端の「新しいグラフ」を選択します。
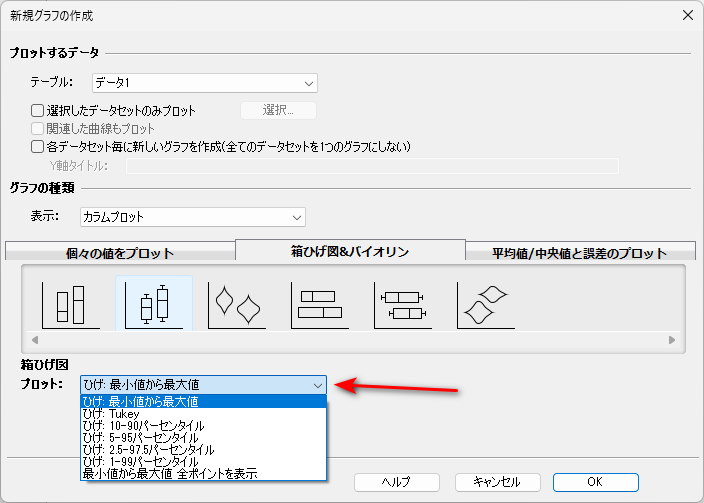
「新規グラフの作成」窓で、「箱ひげ図&バイオリン」タブを選択し、左から 2 番目の箱ひげ図を選択します。
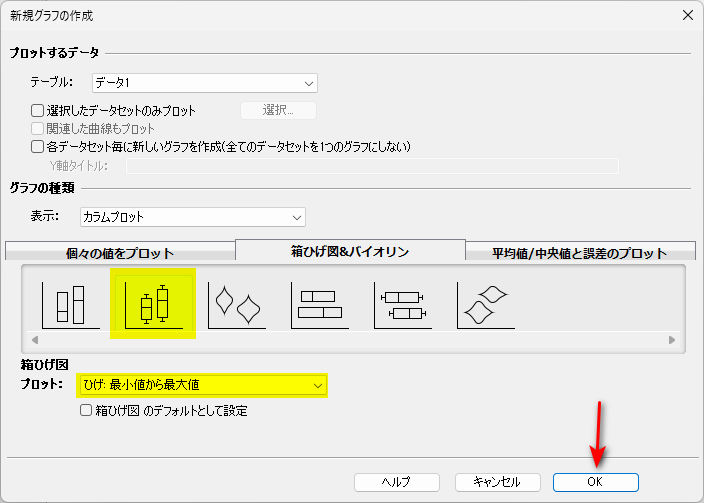
プロット:は、「ひげ:最小値から最大値」を選択しておきます。
OK をクリックすると、グラフが書かれます。
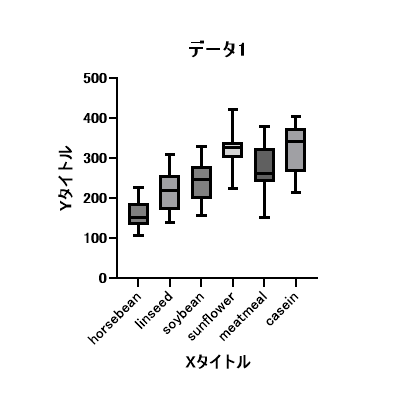
ひげの長さの種類は全部で 6 種類から選べます。
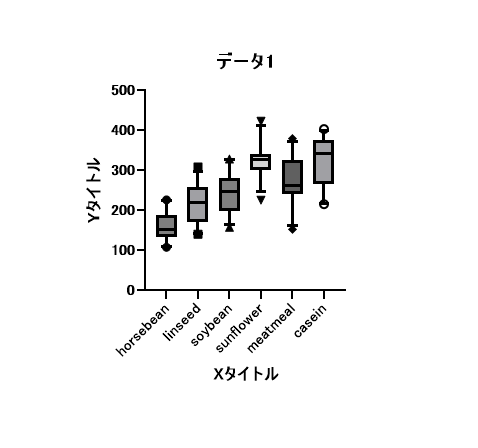
例えば、ひげ: 10-90 パーセンタイルを選択すると、以下のように、ひげからはみ出す飛び離れたデータ点がプロットされます。
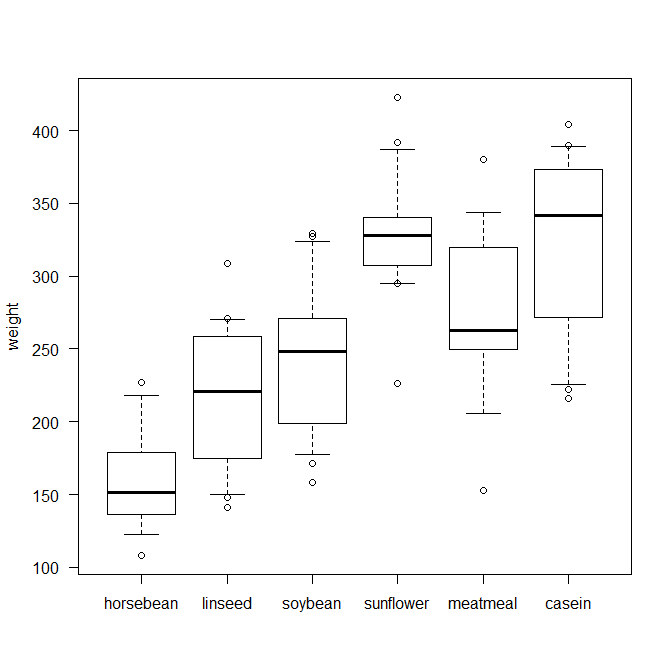
この 10-90 パーセンタイルのひげは、EZR の標準仕様です。
ちなみに、R の標準は、四分位範囲(interquartile range, IQR)の 1.5 倍という設定です。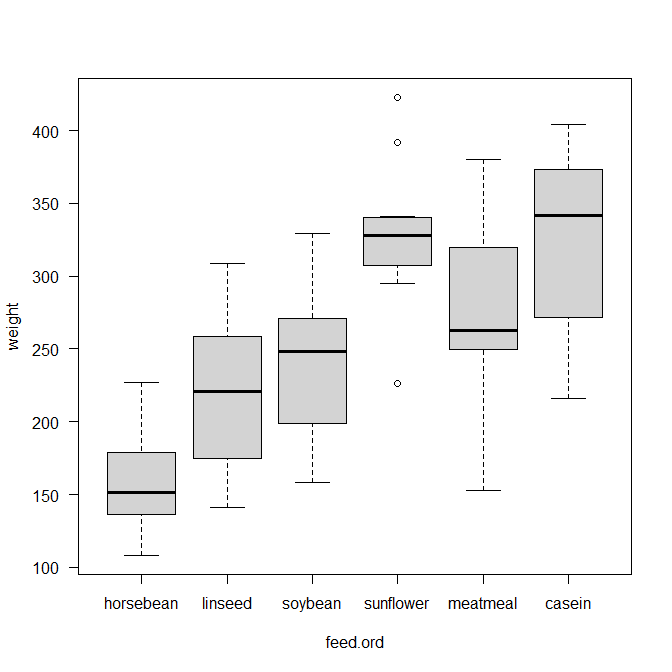
SPSS の箱ひげ図も、IQR の 1.5 倍という設定が標準です。
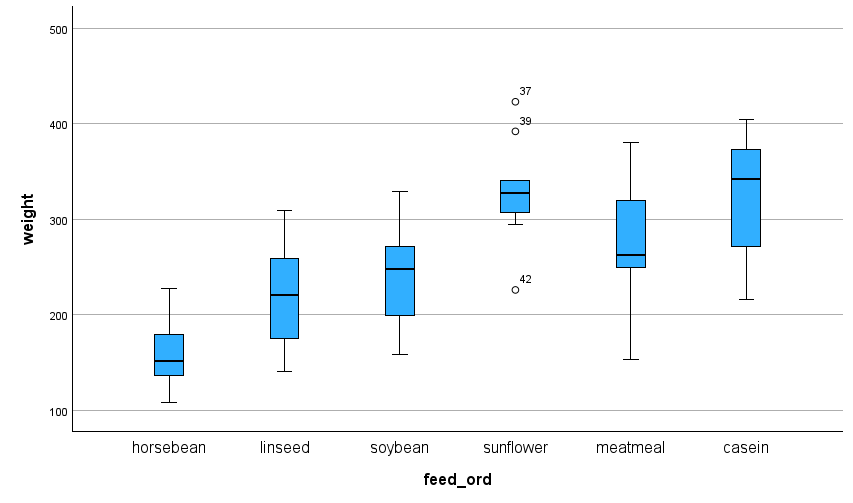
どれが絶対的に正しいということはないので、問われたときにきちんと説明できるようにしてあれば、大丈夫です。
GraphPad Prism のグラフに戻ります。
以下の黄色ハイライト部分のタイトルなどは変更できます。
クリックして、タイトルなどを書き入れると以下のようになります。
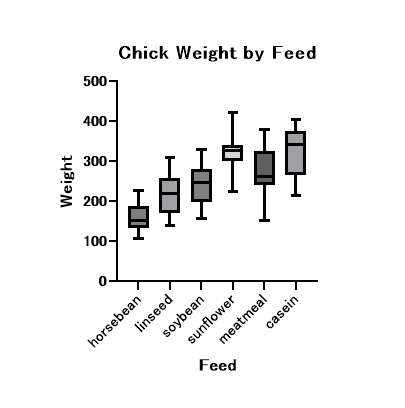
最後に、このグラフに検定結果の「*」を入れていく方法をご紹介します。
上部のリボン部分に、図形というセクションを見つけて、「*」マークをクリックします。
別の解析を先に実施していると、ペアごとの比較結果の形式窓が開きます。
ここで、「Kruskal-Wallis 検定 — データ 1」を選択して、OK をクリックします。
「外観」と「グラフの比較」タブが現れるので、「外観」タブを選択します。
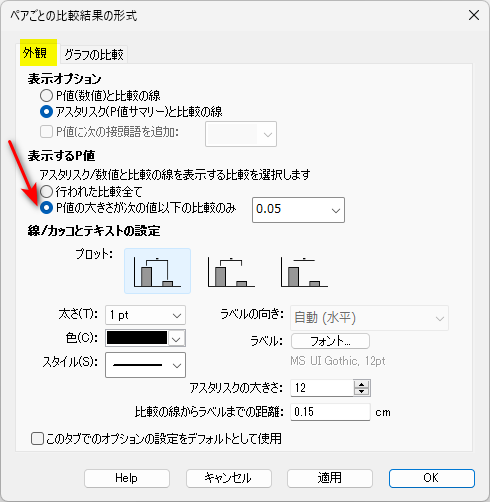
「外観」タブで、「表示する P 値」セクションの、「P 値の大きさが次の値以下の比較のみ 0.05」を選択します。
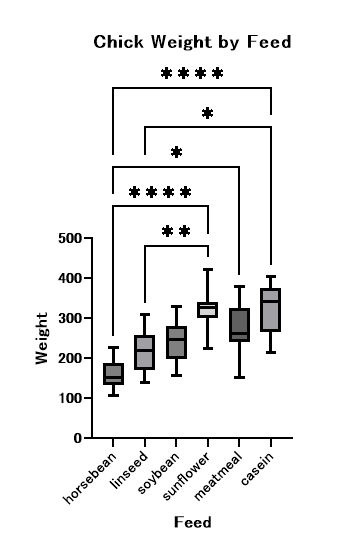
OK をクリックすると、統計学的有意な群間のみに、「*」マークがついて、グラフが完成します。
GraphPad Prism で Friedman 検定を実施してグラフを書く方法
Friedman 検定のためのデータ準備
Friedman 検定は、ノンパラメトリック版反復測定分散分析です。
データの入力方法は、Kruskal-Wallis 検定と同じく、カラムプロット形式で入力します。
入力方法は、こちらの反復測定データの入力と同じなので、参考にしてください。
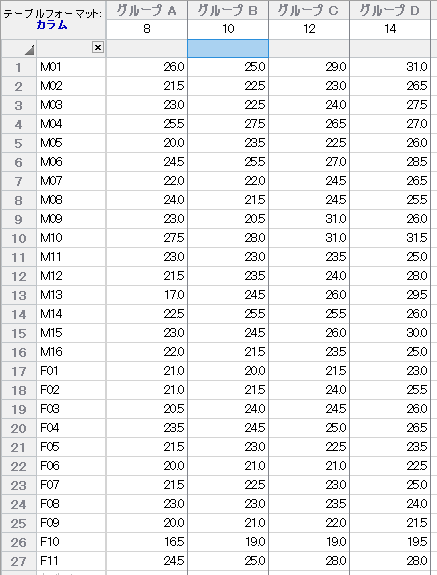
以下のように、データを入力します。
縦方向に、対象者が並んでいて、横方向は、複数回反復測定した測定値が並んでいます。
Friedman 検定の実施
Friedman 検定は、左端の「新しい分析」をクリックして、実施します。
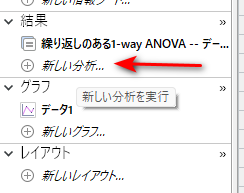
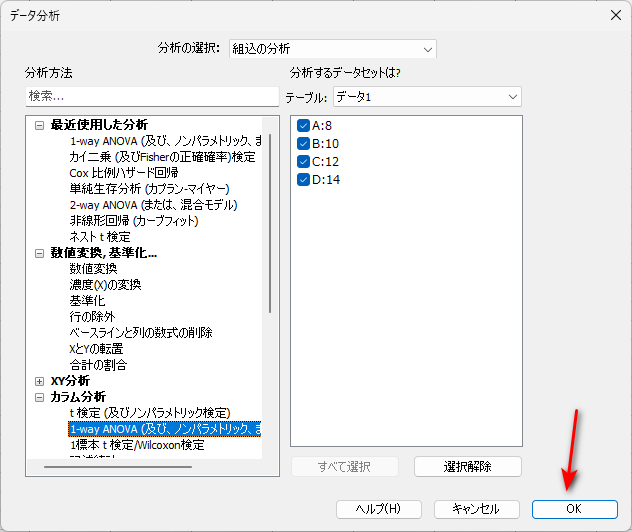
「データ分析」窓で、「カラム分析」の「1-way ANOVA(及び、ノンパラメトリック、・・・」が選ばれていることを確認して、OK をクリックします。
同じデータで分析したことがあると、以下のダイアログボックスが現れます。
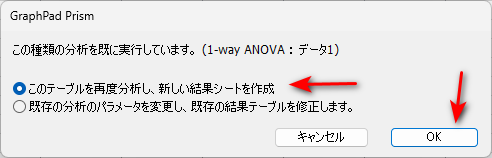
再度分析して、新しい結果シートを作成するほうが選ばれていることを確認して OK をクリックします。
「パラメータ」窓の「実験意図」タブでは、「各行は、マッチしているデータ、又は繰り返し測定データです」を選択します。
また、残差のガウス分布仮定は、「いいえ、ノンパラメトリック検定を行う」を選択します。
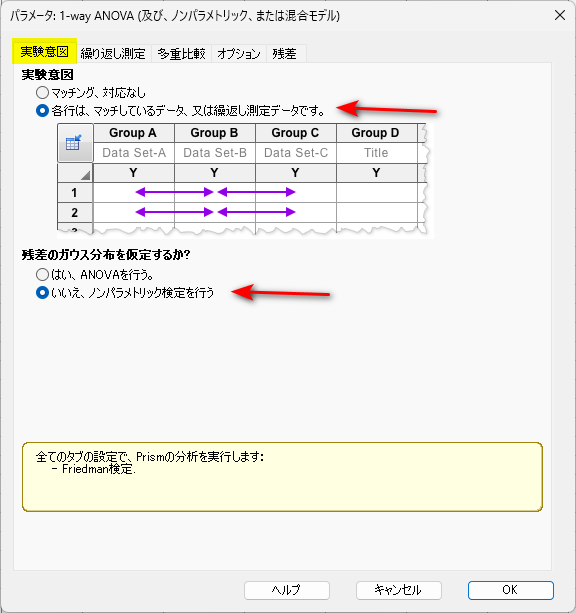
「繰り返し測定」タブは、特に選択することはなく、次のタブに移ります。

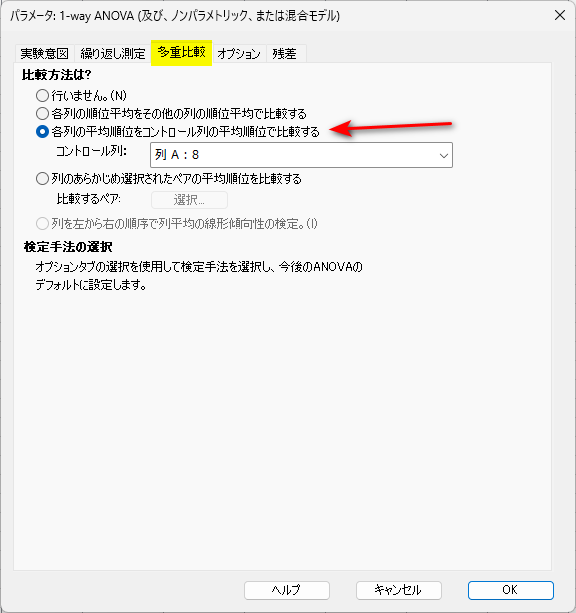
「多重比較」タブでは、「各列の平均順位をコントロール列の平均順位で比較する」を選択します。
この選択肢は、ベースラインとの比較を行う方法です。
このとき、総当たりで比較したい場合は、「各列の順位平均をその他の列の順位平均で比較する」を選択します。
「オプション」タブでは、多重比較検定として「多重比較の修正:統計的な仮説検定を使用(推奨)検定:Dunn」を選択します。
Dunn 検定の文献情報は、こちらです。
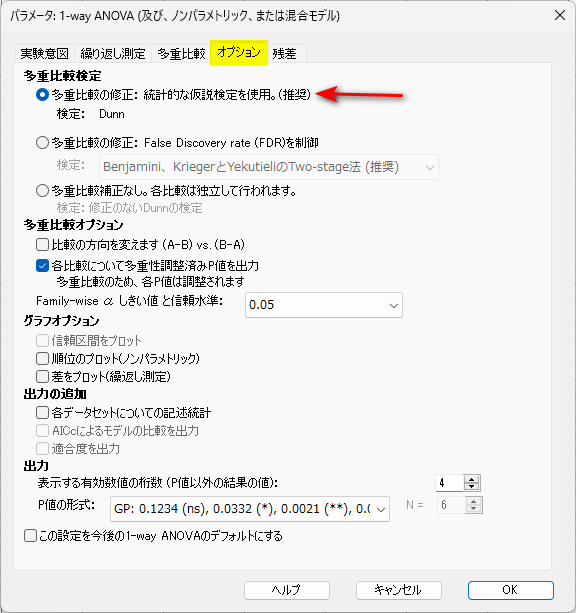
OK をクリックすると、検定結果が表示されます。
Friedman 検定は、P <0.0001 と、どの時点も差がないという帰無仮説が棄却されて、統計学的にいずれかの時点が異なることが示されました。
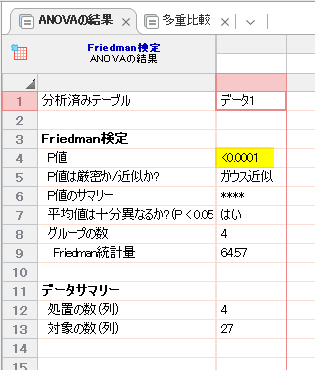
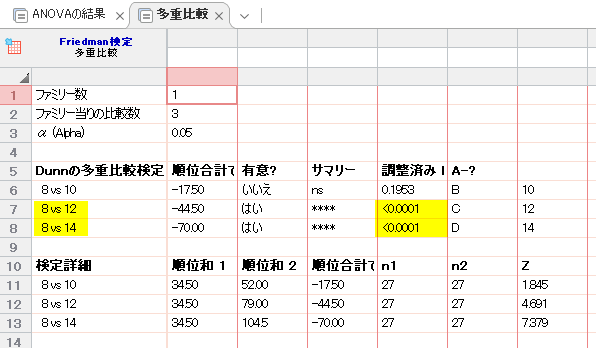
多重比較タブをクリックすると、Dunn の多重比較検定の結果が表示されます。
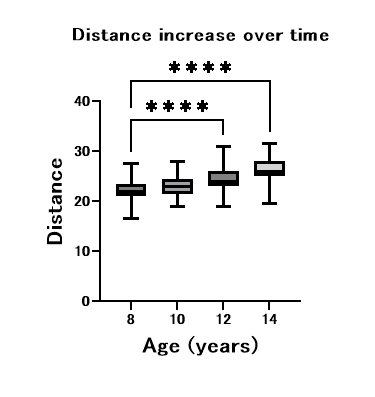
8 vs 12, 8 vs 14 の比較が、いずれも P <0.0001 で統計学的有意に異なることが示されています。
グラフの書き方と検定結果の書き入れ方
グラフを書くには、左端の「新しいグラフ」をクリックして作成します。
「新規グラフの作成」窓が開いたら、「箱ひげ図&バイオリン」セクションをクリックします。
左から二番目の箱ひげ図を選択し、「ひげ:最小値から最大値」が選ばれていることを確認します。
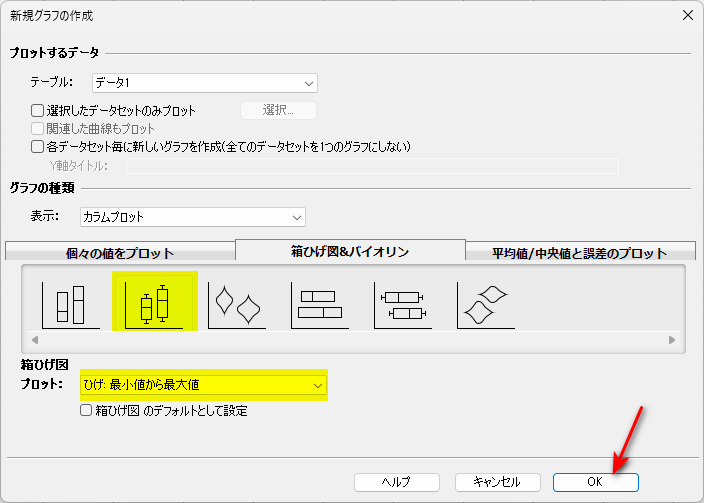
OK をクリックすると、グラフが書かれます。
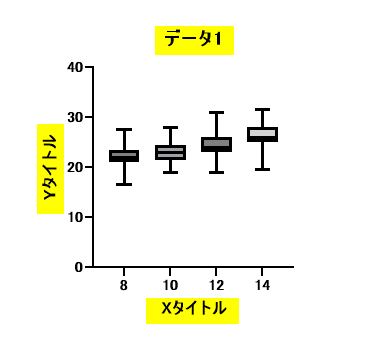
黄色ハイライト部分をクリックするとタイトルが変更できます。
タイトル、軸ラベルを変更したら、あと少しで完成です。
最後に、グラフに先ほどの検定結果の「*」を書き加えるために、上部リボンの「図形」から「*」をクリックします。
分析結果が複数ある場合は、グラフにする分析を選ぶ窓が出てくるので、「Friedman 検定 — データ 1」を選択して、OK をクリックします。
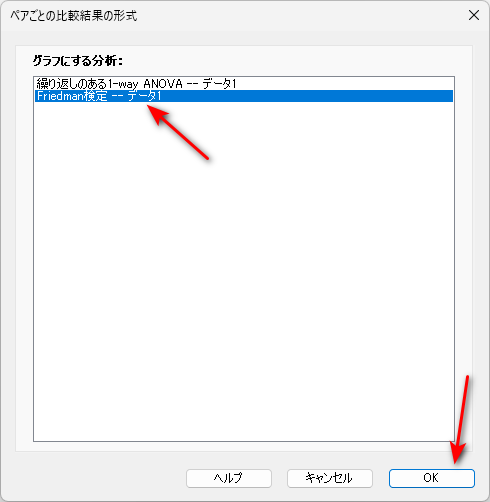
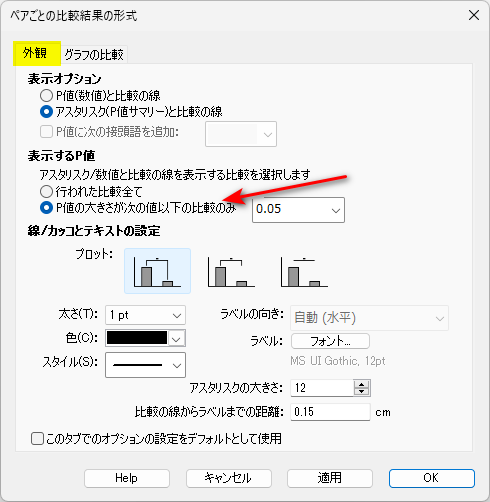
「ペアごとの比較結果の形式」窓内の「外観」タブをクリックします。
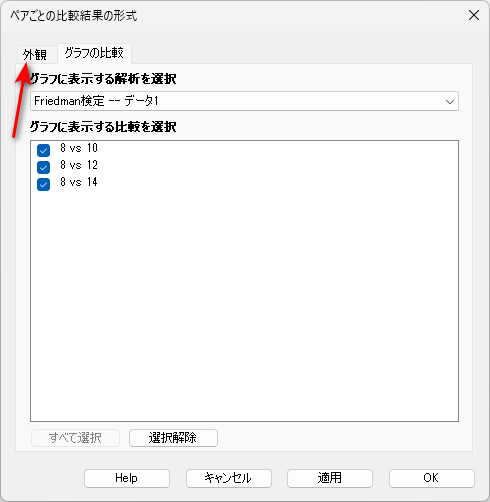
「表示する P 値」の「P 値の大きさが次の値以下の比較のみ 0.05」を選択して、OK をクリックします。
統計学的有意な差が検出された比較のみに「*」がつきました。
これで、グラフの完成です。
まとめ
簡単きれいに論文掲載品質のグラフが作成できる GraphPad Prism で、Kruskal-Wallis 検定、Friedman 検定、及びそれぞれのグラフ作成の方法を紹介しました。
ノンパラメトリックな方法は、平均値や標準偏差を使わないため、それに合わせて中央値や四分位範囲を用いる箱ひげ図で、グラフ表現してみました。
GraphPad Prism を使うと、3 群以上の検定も多重比較もいっぺんに実施できて、グラフにもすぐに書き入れることができるので、研究発表のプレゼンにも、論文の図にも最適です。
まだ、試したことがない人は、一度試してみてはいかがでしょうか?










コメント