薬剤や治療法の効果検証といった典型的な介入研究では縦断的に、同一被験者群の事前(pre)と事後(post)を比較することもあります。
これに加えて、介入の効果が持続しているかどうか、追跡調査をするケース(follow up)もよく見られるかと思います。
このように、同一被験者に対し、繰り返し測定したデータを比較検証する手法にフリードマン検定があります。
今回の記事ではフリードマン検定について解説していきます。
フリードマン検定は反復測定データを解析する手法!

フリードマン検定は反復測定データを解析する手法なのですが、そもそも反復測定データとはどんなデータでしょうか?
反復測定データとは?
下のデータは、ある運動療法の効果を検証するために、腰背部痛を抱える高齢者10名にその運動療法の前(Pre)後(Post)と経過観察後(Follow up)の3時点で痛みのスケールであるFRS (Face Rating Scale)を観測したものです。
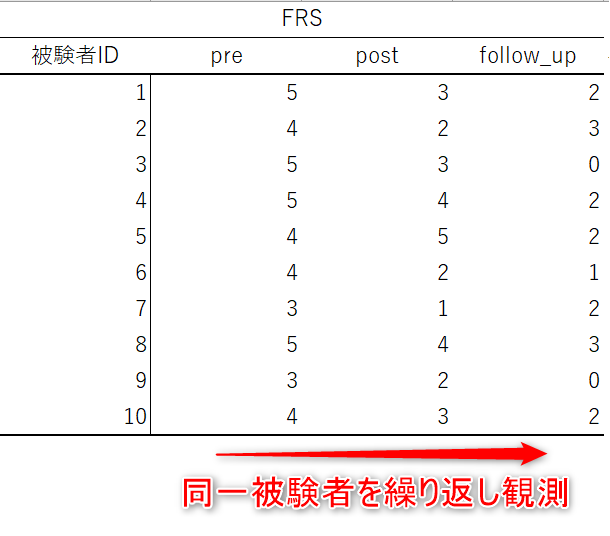
このように同一の被験者から複数回観測したデータを「反復測定データ」あるいは「対応のあるデータ」と呼びます。
反復測定データは同一の被験者からのデータが集積しているので、各時点の値に注目するというよりも、各被験者がどのように変化していったという観点で比較をすることができます。
例えば、1の被験者は、運動療法前に5の痛みを訴えていたものが療法後には3に軽減し、経過観察後はさらに2まで軽減したと評価することができます。
反復測定データを解析する手法の一つがフリードマン検定!
このような反復測定データについて、統計的仮説検定を行う場合、方法論には大きく分けて2つあります。
ひとつは、観測されたデータの値そのものの変化を問題にする方法。
平たくいうと、被験者ごとにその平均値からどのくらい増減しているかに着目します。
そして、各時点における平均値との差の大小を比較するという方法です。
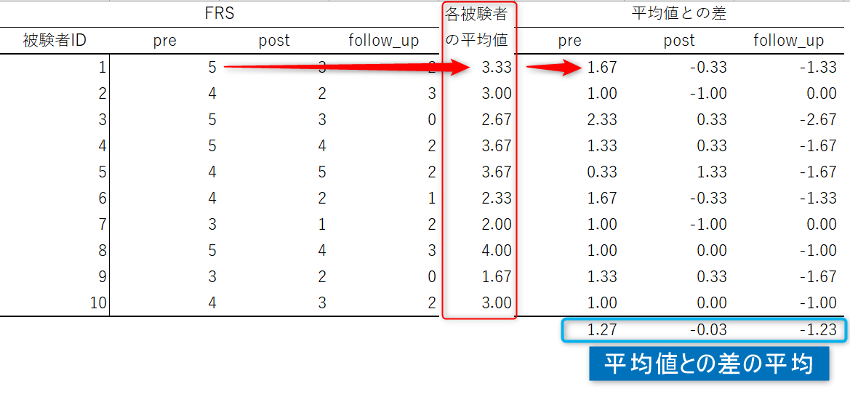
反復測定分散分析(Repeated Measures ANOVA)と呼ばれる手法はこのような発想の上に成り立っています。
もうひとつは、観測されたデータの順位を問題にする方法です。
被験者ごとに観測値を小さい順に順位付けをし、各時点の平均順位を比較するという方法です。
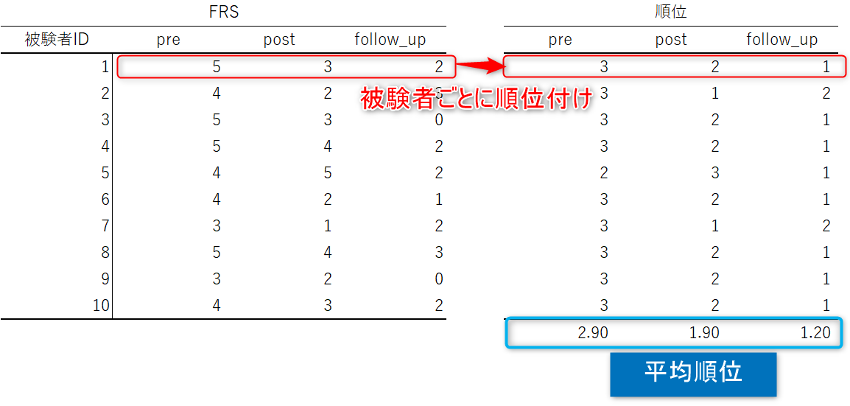
フリードマン検定はこのように、順位の発想の上に成り立っています。
反復測定分散分析とフリードマン検定の違い
上記で学んだように、反復測定分散分析とフリードマン検定は、いずれも対応のあるデータ間の差を検証するためのものです。
反復測定分散分析は観測値そのものを対象とし、平均値の差を問題としていますので、正規性を仮定したパラメトリックな方法となります。
それに対し、フリードマン検定は順位付けをすることで観測値そのものからは離れることになるので、観測値の分布を問題としないノンパラメトリックな方法になります。
分散分析が平均値を考えるパラメトリック検定であり、クラスカルウォリス検定が順位を考えるノンパラメトリックと同じような関係ですね。
フリードマン検定の計算方法や手順は?なぜ順位を考えるのか?
フリードマン検定は順位に換算していましたが、なぜ順位付けなどするのでしょうか?
その意味を知るために順位付けのパターンについて、先ほど示したFRSのデータで考えてみましょう。

上の例のような、3時点観測の場合、各被験者に3つのデータが存在するので順位付けをすると、3つのデータは必ず1, 2, 3のいずれかの順位に変換されます。
(観測値が同じ値の場合には、割り当てられる順位の平均に変換する。例えば、1位と2位が同じ値ならば、1.5位にする。)
このとき、各被験者の順位データは合計すると必ず6となります。
この必ず6になるというのが重要で、合計が固定されていると平均値も固定されます(この場合は順位の平均値は必ず2になる)。
また、1, 2, 3が必ずひとつずつ出現するので分散も固定されます(同順位のある場合でも一定の値に固定される)。
このように、順位付けすることで、平均値や分散を固定することができます。これは観測値そのものがどのような分布になっていようとも成立しますので、分布を仮定せず検定できることになります。
被験者ごとに順位の合計が固定されるということは、被験者全体での順位の合計も固定されることになります。
上の例では被験者は10名ですので、被験者すべての順位を合計すると必ず60となります。
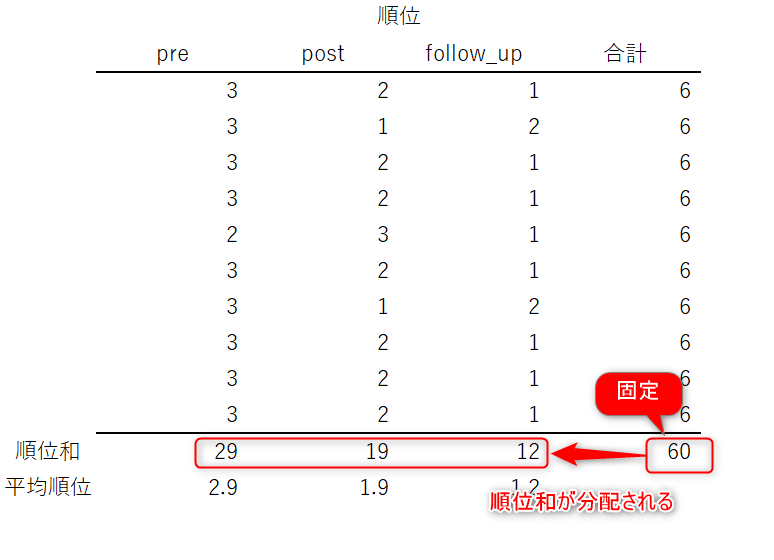
そして、各時点の順位の合計はすべての順位の合計が分配されたものと捉えることができます。このように順位を足し合わせたものを順位和と呼びます。
フリードマン検定の帰無仮説と順位和
フリードマン検定は反復測定データを順位付けし、群の違い(上の例では各時点)によって順位和(または平均順位)が異なると言えるかを検証する仮説検定です。
したがって、
帰無仮説は、「群の違い(時点の違い)によって値の位置は変わらない。」となり
対立仮説は、「群の違い(時点の違い)によって値の位置は変わる。」となります。
観測値そのものではなく順位付けしたものを扱うため、仮説の表現が多少抽象的になる点に気をつけましょう。
フリードマン検定のカイ二乗統計量への近似
帰無仮説が正しいとすれば、順位和は均等に分配されるはずです。
上の例であれば、各時点の順位和は20 (60÷3)となり、平均順位は2 (20÷10)となるはず。
観測された平均順位がこの2からどの程度ズレているかに注目し、被験者全体の順位の合計が固定されていることにより求まる分散を用い、さらに、平均順位に対して、中心極限定理を援用することで、カイ2乗検定と同様にカイ2乗分布に近似させて検定するのがフリードマン検定になります。
このような処理により、検定統計量は
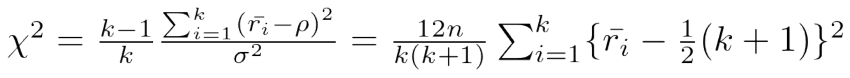

となり、自由度 (k-1)のカイ2乗分布を用いてp値を計算します。
フリードマン検定の結果の解釈は?有意差があったときどんな結論?
上の運動療法の例について、SPSSを用いてフリードマン検定を行うと以下の結果が得られました。

有意差が認められ、帰無仮説が棄却されるということ。
すなわち、pre, post, follow up の違いで、FRSの値に統計的にみて有意差があるとなります。
有意差があるということは対立仮説を採択することになり、「群の違い(時点の違い)によって値の位置は変わる。」となりますね。
フリードマン検定の結果の解釈に関して注意点
ここまで見てきたように、フリードマン検定は観測値を順位に変換して検定しています。
順位に変換するということは、観測値そのものとは異なるものを比較していることになります。
したがって、反復測定分散分析のように、平均値に有意な差があったとは言えない点は注意しましょう。
あくまで、群によって平均順位が異なるということしか言えないので、信頼区間を用いて、具体的にどの程度の違いがあるなどという議論はできません。
ノンパラメトリックな検定であるフリードマン検定は、順序尺度以上のどのような量的変数に対しても使用できるというメリットがあります。
しかし、時点によって変化が認められるというレベルの話までしかできず、具体的な差を論じることができないという点で、パラメトリックな検定よりは使いにくいかもしれません。
そのため、検定結果だけではなく要約統計量やグラフ化を用いて、臨床的に意味のある差が出ているのかどうかは、全体的に判断する必要があります。
まとめ
同一の被験者集団に対する縦断的調査のような反復測定データについて、観測値の分布を考慮せずに使用できるのがフリードマン検定です。
群間で有意な変化があったと言えるか否かを判断する上で、もっともシンプルな統計的仮説検定。
しかし、結果から分かることは限定的ですので、使用場面や論文等への記述方法には注意して使用しましょう。
>>GraphPad Prism で Kruskal-Wallis 検定 Friedman 検定を実施してグラフを書く方法











コメント