「Coxモデルでは解析できないって、どういうこと……?」
生存時間解析の定番といえばCox比例ハザードモデルですが、現実のデータはそんなに単純ではありません。
例えば、再発が何度も起きる疾患や、研究に参加する前からリスクが始まっていた人(=左側打ち切り)など、1回だけのイベントに収まらないケースは少なくありません。
そんなときに力を発揮するのが、Andersen-Gill(AG)モデルです。
本記事では、「左側打ち切りとは何か?」「Coxモデルではなぜ対応できないのか?」「Andersen-Gillモデルの考え方と実装方法」までを、統計初学者でも理解できるように、やさしく・ていねいに解説していきます。
Rでのサンプルコード付きなので、再発データの解析を始めたい人にも実践的な一歩となる内容です。
左側打ち切りデータとは何か?
生存時間解析というと、一般には「ある出来事がいつ起きるか」を予測・説明する統計手法のことを指します。
たとえば「がん患者が再発するまでの期間」「機械が故障するまでの稼働時間」など、イベントのタイミングに注目します。
ですが実際のデータ収集では、全ての事象を最初から最後まで観察できるとは限りません。そんな現実に対応するために生まれた概念が、「打ち切り(censoring)」です。
打ち切りデータとは?3つの分類を押さえよう
まず前提として、「打ち切り」とは“いつイベントが起きたのか正確にわからない”という情報のことです。生存時間解析では、この打ち切りのタイプをしっかり理解しておくことがとても重要です。
主に以下の3種類があります。
- 右側打ち切り(Right-censoring)
最もよく使われる打ち切りです。ある対象者について、観察期間中にイベントがまだ起きていないため、「いつ起きるか」はわからない。
例:調査終了時点でまだ再発していない患者。 - 左側打ち切り(Left-censoring or truncation)
観察を開始した時点で、すでにイベントが起きていた可能性があるが、いつ起きたかは不明。
例:健康診断で糖尿病と診断されたが、いつから糖尿病だったか不明。 - 区間打ち切り(Interval-censoring)
イベントがある期間内に起きたことはわかるが、正確な時点がわからない。
例:年1回の健康診断で、前回は異常なし、今回は陽性=その間に発症した。
左側打ち切りが起きやすい状況とは?
左側打ち切りは、過去の履歴を持つ被験者や対象者を途中から観察する場面でよく発生します。以下のようなケースを想像すると、理解しやすいかと思います。
臨床研究の例
ある研究が「心疾患の初発までの期間」を調べるものだとします。ところが、すでに症状を経験している患者も、研究参加時には「治療中」や「経過観察中」だった場合、いつ心疾患が起きたかが記録されていないことがあります。
このように「いつ発症したか」がわからないデータが含まれると、初発までの正確な時間が不明になります。
なぜ左側打ち切りが分析を難しくするのか?
左側打ち切りがあると、「本来の観察開始時点が欠けている」ことになります。
つまり、生存時間(eventまでの時間)を過小評価してしまう可能性があるのです。
たとえば、ある患者が研究参加前に糖尿病を発症していたとします。
でも私たちは「参加時点で糖尿病である」ことしか知らないので、「糖尿病になったのは、研究に参加してから」と誤解してしまうリスクがあります。
これは生存時間解析の根幹――「イベントの発生時刻と、それに至る時間をどう扱うか」――において、非常に深刻なズレを生む原因になります。
左側打ち切りデータは、Coxモデルでは対応できない?
Cox比例ハザードモデルは、右側打ち切りには標準的に対応できますが、左側打ち切りには対応できません。なぜなら、モデルが前提としているのは、「全ての対象が同じ基準時点(スタート)から追跡される」という条件だからです。
この前提が崩れると、ハザード比の推定やサンプルの扱いにバイアスが生じ、誤った因果関係や効果の大きさが導かれてしまう恐れがあります。
左側打ち切りを完全に避けるのは難しい
現実のデータ分析では、完璧な情報を持った「理想的な被験者」ばかりを揃えることはできません。特にレトロスペクティブ研究(過去の記録に基づく研究)や、電子カルテのような“途中から収集されたデータ”では、左側打ち切りは避けがたい問題です。
ここで登場するのが、再発や時間依存共変量を扱える「Andersen-Gillモデル」です。このモデルを使えば、観察開始時点を“0”とし、そこからの再発イベントを扱うという構造がとれるため、左側打ち切りの影響を最小限に抑えることが可能です。
言い換えれば、「本当のスタート時点が不明でも、観察開始からのデータを活かしてモデル化する」柔軟な方法を与えてくれるのです。
左側打ち切りデータは、「すでにイベントが起きていたかもしれないけど、それがいつだったのか不明」という、実務上とてもよくあるデータ状況です。そしてこれに対応するには、単純なCoxモデルでは不十分。再発や時間依存性を考慮した解析手法の出番です。
Cox比例ハザードモデルでは足りない場面
生存時間解析の代表的な手法といえば、やはり「Cox比例ハザードモデル」が有名です。多くの教科書でも最初に登場し、RやPythonなどの統計ソフトにも標準で実装されています。
では、なぜこのCoxモデルだけでは不十分な場面があるのでしょうか?
この章では、Coxモデルの基本を復習したうえで、現実のデータにおける「限界」と、それを補う必要性について丁寧に解説します。
Coxモデルとは?ざっくり復習
Cox比例ハザードモデル(Cox Proportional Hazards Model)は、生存時間と共変量の関係を調べるためのモデルです。
このモデルのポイントは、「特定の変数がハザード(イベントが起きる確率)にどの程度影響するか」を、ハザード比(Hazard Ratio, HR)という形で示せることです。
ここでの「比例」とは、「リスクの形は変えずに高さだけを変える」=共変量が時間によらず一定の影響を持つ、という意味です。
現実には「1回で終わらないイベント」も多い
さて、ここで想像してみてください。たとえば次のようなデータです。
- がんの再発を追う医療研究
- うつ病の再発調査
- 工場での機械トラブル(何度も壊れる)
- 企業の従業員が何度も休職するケース
これらはいずれも「1人(あるいは1台、1事象)につき、複数回イベントが起きる」タイプのデータです。
ところが、Coxモデルではこのような「複数回のイベント(recurrent events)」には原則として対応できません。
なぜなら、Coxモデルの基本的な単位は「1人あたり1回のイベントを記録する」というものだからです。
たとえば、1人の患者が3回再発した場合、Coxモデルでは最初の再発しか扱えず、それ以降の再発データは無視されてしまいます。これでは、せっかくの貴重なデータを捨ててしまうことになりますよね。
「時間とともに変わる変数」にも対応しにくい
もうひとつ、Coxモデルの限界として挙げられるのが、「時間依存性共変量(time-dependent covariates)」の取り扱いです。
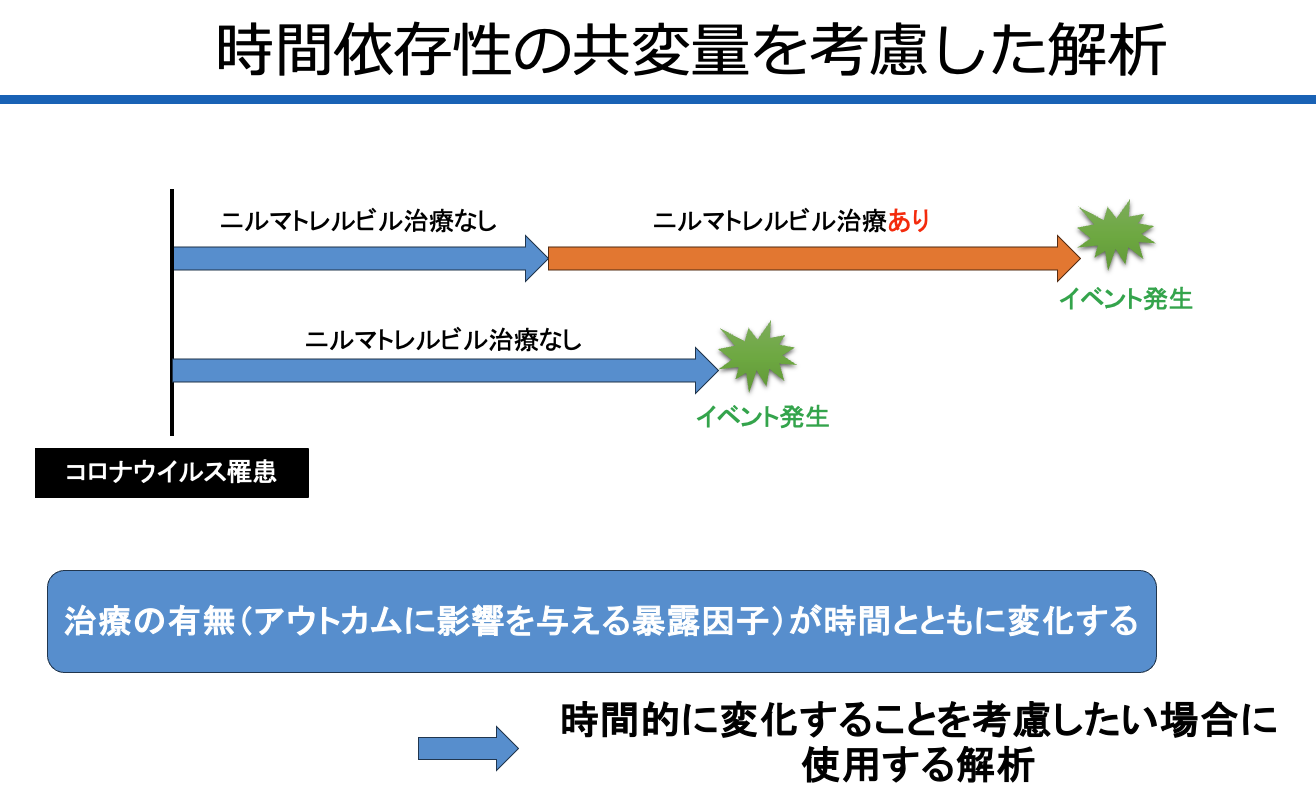
現実のデータでは、治療内容や生活習慣、環境条件などが時間とともに変化することは珍しくありません。たとえば:
- 「途中から薬を飲み始めた」
- 「退院して在宅療養に切り替わった」
- 「会社の制度が変わった」
このような変化があると、共変量が時間の経過とともに変わってしまい、単純なCoxモデルでは“1つの値”として入力できません。
これを無視すると、推定に大きな誤差が生じたり、リスクの因果関係を見誤る恐れがあります。
左側打ち切りとCoxモデルの相性
さらに、前のセクションでも解説した「左側打ち切り」もCoxモデルにとっては厄介です。
Coxモデルは、「全員が同じ時点から観察されている(=スタートが揃っている)」という前提で設計されています。そのため、観察開始前にすでにイベントが起きていたかもしれない人(=左側打ち切り)を含めると、生存時間の計算がおかしくなってしまうのです。
結果として、解析対象から外さざるを得ず、サンプルサイズが減ったり、バイアスが生じたりすることもあります。
このように、Coxモデルは生存時間解析の基本中の基本ではありますが、現実のデータ構造――特に次のような状況――には対応が難しいです。
- 1人が複数回イベントを経験する(再発)
- 時間とともに変わる共変量を扱いたい(処置・環境)
- 左側打ち切りが存在する(初発タイミングが不明)
これらの課題に柔軟に対応できるモデルとして登場したのが、Andersen-Gillモデルです。
このモデルはCoxモデルの枠組みを活かしつつ、時間依存性や再発を「カウントプロセス」としてモデル化することで、より複雑な現実のデータに対応することができます。
Andersen-Gillモデルって何?ざっくり解説
前のセクションで、Cox比例ハザードモデルには「1回限りのイベントしか扱えない」「時間とともに変化する変数に弱い」といった限界があることを解説しました。
現実のデータには、1人の患者が何度も再発したり、環境や治療状況が変化したりするケースが数多くあります。
そうした複雑な状況に対応するために開発されたのが、Andersen-Gill(AG)モデルです。
このセクションでは、AGモデルが何を解決してくれるのか、Coxモデルとどう違うのか、初心者でも理解しやすいようにやさしく紹介します。
Andersen-Gillモデルとは?
Andersen-Gill(AG)モデルは、再発や複数イベントを解析するための拡張Coxモデルです。
1970年代末にAndersenとGillによって提案され、Coxモデルの考え方をベースにしつつ、「1人の対象に複数のイベントが起きる」ことを前提に設計されています。
最大の特徴は、「Counting Process(カウントプロセス)」という考え方を取り入れている点です。
これは、1人の対象を“時間帯ごとのイベントのまとまり”として捉えるアプローチであり、時間依存性共変量や複数イベントにも対応可能です。
Andersen-Gill(AG)モデルはどんな場面で使えるの?
AGモデルは、以下のような繰り返しイベントのある研究にとても適しています。
- 医療:がんや心疾患の再発、再入院、感染症の再感染
- メンタルヘルス:うつ病エピソードの再燃
- 行動研究:犯罪者の再犯や交通違反の再発生
- ビジネス:ユーザーのサービス再利用、顧客の離脱と復帰
- 工業・IT:機械の再故障、システム障害の再発
どれも1回で終わるわけではなく、複数回発生しうるイベントですよね。AGモデルは、まさにこういった「繰り返し」の構造をモデルとして自然に取り入れることができるのです。
Andersen-Gill(AG)モデルはデータの構造がカギ:「start-stop」形式
AGモデルでは、Coxモデルと異なり、1人のデータを複数行に分割して記録する必要があります。
たとえば、1人の患者が3回再発した場合、次のような構造になります。
| id | start | stop | event | treatment |
| 1 | 0 | 50 | 1 | 0 |
| 1 | 50 | 100 | 0 | 1 |
| 1 | 100 | 150 | 1 | 1 |
このように、「start」から「stop」までの期間を1単位として、各期間でイベントが発生したか(event = 1)を記録します。
治療内容(treatment)などの共変量も、期間ごとに変更できます。これにより、「時間依存性共変量」も自然に組み込むことができます。
AGモデルの根本的な考え方は、Coxモデルの数式に基づきつつ、「再発イベントも含めて、全部“1つのデータ”としてまとめて解析する」というアプローチです。
1人の対象に複数のイベントがあると、それらは独立ではありません。最初の再発が次の再発に影響を及ぼすことはよくあります。
AGモデルでは、この依存性に対応するために、「クラスタリング(cluster)」というテクニックを用います。
Rで実装する際には、cluster(id)のように指定することで、個人ごとのイベントの相関を考慮し、標準誤差の過小評価を防ぐことができます。
Andersen-Gill(AG)モデルは左側打ち切りにも強い
AGモデルは、「観察開始時点からの再発イベントを扱う」という構造を取るため、左側打ち切りにもある程度対応できます。
たとえば、すでに糖尿病を発症している患者が研究に参加した場合、その人の「初発」はわかりませんが、「参加後の再発」は記録できます。
AGモデルは、そういった“再発だけ”を扱う設計なので、左側打ち切りの人も解析対象として含めやすいのです。
Andersen-Gillモデルの使いどころと注意点
ここまでで、Andersen-Gill(AG)モデルが「再発や時間依存性共変量に強い」という特徴を持つことがわかってきました。
しかし、「このモデルは便利そうだから、とりあえず使えばOK!」というわけではありません。
すべてのケースで万能ではないからこそ、「どんなときにAGモデルを使うべきか?」「どんな点に注意すべきか?」をしっかり押さえておくことが大切です。
このセクションでは、他のモデルとの比較を交えながら、AGモデルの適用場面と注意点について丁寧に解説していきます。
まずは整理:似ているけど違うモデルたち
繰り返しイベントのあるデータを扱う手法はいくつかあります。Andersen-Gillモデルはその一つにすぎません。以下のような他の方法ともよく比較されます。
| モデル名 | 対応できる特徴 | 主な想定 |
| Cox比例ハザードモデル | イベント1回/時間依存性× | 最初の発症まで |
| 時間依存性Coxモデル | イベント1回/時間依存性◯ | 処置や環境が変わる場合 |
| Andersen-Gillモデル | イベント複数/時間依存性◯ | 再発・複数事象があるとき |
| 負の二項回帰モデル | 回数に対応/時間無視 | 期間内のイベント回数だけを知りたい場合 |
AGモデルは、「繰り返しイベント × 時間情報を重視 × 処置の影響も調べたい」といった分析に最適です。
逆に言えば、「イベントは1回しか起こらない」または「イベントの回数だけ知りたい」場合には、他のモデルの方が適していることもあります。
Andersen-Gillモデルを使う際の注意点
便利なAGモデルですが、注意すべき点もいくつか存在します。とくに次のようなポイントは、初心者でも押さえておくべき重要な項目です。
イベント間の独立性を仮定している(が、実際は依存している)
AGモデルは、1人の対象におけるイベント(例:再発1回目、2回目、3回目)を、統計的に独立しているものとして扱います。しかし実際には、1回目の再発が2回目のリスクに影響を与えることはよくありますよね?
この「イベント間の依存性」がモデルに無視されるため、標準誤差が過小評価されやすいという問題があります。これを補うためには、cluster(id)で個体ごとの相関を考慮する必要があります。
全体の“ハザード構造”は共有される
AGモデルでは、すべての再発が同じ“ハザード構造”に従うと仮定されます。つまり、「1回目の再発」と「3回目の再発」では、基本的なモデル構造は変わらないとみなされます。
しかし、現実には再発を繰り返すほど病状が重くなったり、対応が変わったりすることもあります。そういった「イベントごとの変化」をモデルに入れたいときには、PWPモデルやfrailtyモデルといった別のアプローチが必要です。
観察期間の分割が必須で、データ加工が大変
AGモデルでは、「start–stop形式」で時間を分割したデータを準備する必要があります。これには手間がかかる上、観察期間の分け方に迷うこともあります。特に時間依存性共変量が複雑になると、手動でのデータ構築が面倒になる可能性があります。
この点は、事前に計画を立ててスクリプト化しておくと作業効率が上がります。
解釈には丁寧さが求められる
AGモデルの出力結果は、Coxモデルと同様に「ハザード比(HR)」として出てきます。ただし、1人あたり複数のイベントを対象としているため、そのHRが示す意味合いも少し複雑になります。
たとえば、「治療Aがハザードを30%下げる」という結果が出た場合、それは再発全体に対する効果であり、1回目か2回目かを区別した効果ではありません。
RでAndersen-Gillモデルを実装する
ここまでで、Andersen-Gillモデルの理論や使いどころについて詳しく学んできました。では、実際にRでこのモデルをどのように実装すればよいのか? 初心者にもわかりやすく、具体的なコード例とあわせて解説していきます。
ポイントは、「start–stop形式でのデータ構造」と「cluster()による個体内相関の考慮」です。
Andersen-Gillモデルは、Rの標準的な生存時間解析パッケージである**survival**に組み込まれています。まずは必要なライブラリを読み込みましょう。
install.packages("survival") # 初回のみ
library(survival)次に、AGモデルを使うには、データを「start–stop形式」に整える必要があります。これは、時間区間ごとに行を分けて記録する形式です。
例として、以下のような再発データを想定しましょう。50例分のサンプルデータを作成しています。
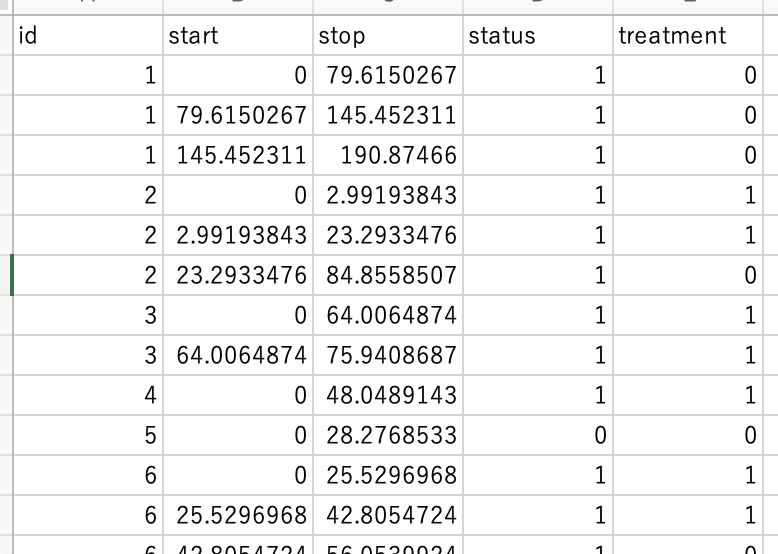
このように、1人の対象者が複数行で表されている点が重要です。それぞれの行が、ある期間中の情報(start〜stop)を記録しています。
生存時間のオブジェクトには Surv() を使います。AGモデルでは「start, stop, event」の形式を取り、coxph() で回帰を実行します。
cox_model <- coxph(
Surv(start, stop, status) ~ treatment + cluster(id),
data = example_data #example_dataという名前でRにインポートしている場合
)
summary(cox_model)ポイント:
- Surv(start, stop, status):期間型のSurvオブジェクト(イベントの発生を時系列で表現)
- cluster(id):同じ対象者(id)内の相関を考慮し、標準誤差の過小評価を防ぐ
- treatment:共変量(時間依存性を含めることも可能)
summary(cox_model) を実行すると、以下のような出力が得られます:

この結果は、「treatmentを受けた期間は、受けていない期間に比べて再発のハザードが2.2%上昇する」という意味になります(HR = 1.022)。exp(coef) がハザード比です。
ここで注意してほしいのは、これは「再発全体に対する平均的な影響」であり、「1回目だけ」とか「2回目に特化した効果」ではない点です。
時間依存性共変量も使える
たとえば、treatment が「途中から開始される」ような状況では、行ごとに値を変えれば、時間依存性共変量として自動的に反映されます。
これはCoxモデルでも Surv(start, stop, status) 形式を使えば可能ですが、イベントが1回しか扱えないという制限があるため、AGモデルの方がより柔軟です。
Q&A:よくある質問に答えます
ここまでで、Andersen-Gillモデルの理論、使いどころ、実装方法まで学んできました。
しかし、初学者が実際に解析を始めようとすると、ふとした疑問や混乱にぶつかることも少なくありません。
このセクションでは、講義や実務の現場でよく出る質問をピックアップし、丁寧に回答していきます。初心者がつまずきやすいポイントを一つずつ整理して、理解を深めていきましょう。
Q1. Andersen-Gillモデルでも「ハザード比(HR)」で結果が出てくるの?
✅ はい、出てきます。
Andersen-Gillモデルは、Coxモデルの拡張形です。そのため、回帰係数の解釈はCoxモデルと同じく「ハザード比(HR)」として表現されます。
ただし、対象が「1回きりのイベント」ではなく「複数の再発を含む全イベント」になっている点が異なります。つまり、得られるハザード比は「全体として再発しやすいかどうか」を評価しており、特定の再発順(1回目/2回目など)に限定された効果ではありません。
例:treatmentのHRが0.65 → 治療中は再発のリスクが全体的に35%下がると解釈します。
Q2. Cox回帰も Surv(start, stop, event) で時間依存共変量を扱えるけど、AGモデルとどう違うの?
✅ 最大の違いは、「複数回のイベントを扱えるかどうか」です。
Coxモデルでも Surv(start, stop, status) 形式を使えば、時間依存共変量(たとえば、治療を途中で変更するなど)を扱うことができます。
ただし、Coxモデルは基本的に「1人につき1回のイベント」までしか扱いません。複数のイベントがある人については最初のイベント以外を無視してしまうのが原則です。
一方、AGモデルは「1人につき何回でもイベントを記録して良い」構造になっており、再発や反復事象を解析する際には必須のモデルです。
Q3. 「左側打ち切り」って、結局どう扱えばいいの?
✅ “初発はわからないけど、再発からは観察できる”場合に強いのがAGモデルです。
左側打ち切りとは、「研究参加時点ですでにイベントが起きていたかもしれないが、その時点がわからない」状態です。
Coxモデルでは、スタート時点が揃っていない人を除外する必要がありますが、AGモデルでは再発イベントから解析を始める構造にできるため、「初発が不明でも再発があれば使える」=実質的に左側打ち切りにも対応可能というメリットがあります。
例:初めてのうつ病発症が不明でも、再発時点から記録すればAGモデルに含められる。
Q4. 再発イベントの回数だけに注目したいなら、AGモデルじゃなくてもよい?
✅ はい、その場合は「負の二項回帰モデル」などのカウントデータモデルの方がシンプルです。
AGモデルは「時間と再発の関係」や「治療の効果」を時間軸上で評価するモデルです。もし、再発のタイミングではなく“回数だけ”を分析したいのであれば、Poisson回帰や負の二項回帰モデルの方が向いています。
ただし、これらのモデルでは時間依存性やイベントの順序は無視されるため、「時間の経過が重要」「再発の間隔を評価したい」場合はAGモデルが優れています。
Q5. Andersen-Gillモデルで、イベント間の依存関係はどう処理されている?
✅ 厳密には“していない”。cluster()で補正をかける必要があります。
AGモデルは、「1人の中の複数のイベントは統計的に独立である」という仮定を置いています。実際には、再発1回目の影響が2回目に波及するような依存関係がありますよね。
この“依存性”を補正するために、cluster(id) を指定することで、標準誤差にロバストな修正をかけることができます。これは必須ではありませんが、実務ではほぼ必須と思ってください。
Q6. Andersen-Gillモデルって難しそう。初心者でも使うべき?
✅ 「タイミング」「再発」「処置の変更」に興味があるなら、挑戦すべきです。
たしかにAGモデルは、Coxモデルよりも準備や理解が難しい部分があります。特に「データをstart–stop形式に整える作業」は最初はハードルに感じるかもしれません。
ですが、そのハードルを乗り越えることで、
- 現実の複雑なデータに対応できる
- 有効な再発予測ができる
- 時間依存性をモデルに反映できる
という強力なスキルセットが手に入ります。
実際、多くの医療研究や社会データ分析ではAGモデルが使われており、「実践的な統計解析スキル」として身につけておく価値は非常に大きいです。
まとめ:繰り返す現象と時間の流れを、見落とさずに捉えるために
生存時間解析と聞くと、まず思い浮かぶのはCox比例ハザードモデル。しかし、現実のデータはもっと複雑です。人は何度も病気を再発し、機械は何度も壊れ、状況は時間とともに変わっていきます。
そんな「1回きりでは終わらない現象」と「変化し続ける世界」を丁寧に捉えるためには、Andersen-Gillモデルという視点がとても有効です。
このモデルの強みは以下の通りです:
- 複数のイベント(再発)を1人あたり複数回扱える
- 時間依存性共変量(途中で処置が変わるなど)に対応できる
- 左側打ち切りの人もデータに含めやすい
- Rでの実装が可能で、Coxモデルの延長線上で使える
一方で、すべての問題を自動で解決してくれる「魔法のモデル」ではありません。イベント間の依存性、モデルの前提、データ整形の負荷など、注意すべき点も確かに存在します。
ですが、そうした点を理解したうえでAGモデルを選び、適切に使いこなせるようになると、あなたの統計解析の幅は格段に広がるでしょう。
時間と再発が交差するデータを前にしたとき、この記事の内容を思い出して、柔軟な分析と解釈に役立てていただければ幸いです。
こちらの内容はYoutubeでも解説しております。
ぜひこちらの動画をご覧くださいませ。













コメント