C統計量（C-index）とは？意味・計算方法・AUCとの違いをわかりやすく解説

「C統計量ってAUCと何が違うの？」

統計や機械学習に触れた人なら、一度は疑問に思ったことがあるかもしれません。

特に医療や金融の分野では、AUCと並んでC統計量（またはC-index）がよく登場しますが、初めて耳にした人には馴染みが薄い指標です。

実はC統計量とC-indexはほぼ同じ指標であり、呼び方が分野によって異なるだけです。

この記事では、そんな混乱しがちなC統計量について、以下の流れでわかりやすく解説します。

• C統計量（C-index）の基本的な意味と役割
• ROC曲線やAUCとの違いと関係性
• 計算方法とプログラミングでの実装例
• C統計量を利用する際に注意すべきポイント

特に、C統計量は「予測の順序の正確さ」を測る指標であることが特徴です。

これは単なる的中率とは異なり、モデルが高い確率で正しい順序付けを行えているかを評価するもので、2値分類から生存時間解析まで幅広く使えます。

C統計量（C-index）とは？基本の定義

C統計量（C-statistics）とは、予測モデルが「対象を正しく順位づけできる能力」を数値化した指標です。

例えば、がん患者の生存期間を予測するモデルがあったとします。

このとき、患者Aの予測生存期間が患者Bより長いとモデルが判断し、実際にAのほうが長生きだった場合、それは「順序が正しい（concordant）」といえます。

このような予測と実際の結果が一致する割合を集計したものがC統計量です。

C統計量とC-indexの関係

結論から言うと、C統計量とC-indexは同じ指標です。

どちらも「Concordance index（適合指数）」の概念を指しており、計算方法や解釈は変わりません。

ただし、使われる場面や分野によって呼び方が異なる傾向があります。

このように、呼び方は異なりますが「予測の順序をどれだけ正しく当てられるか」を表すという本質は変わりません

したがって、論文やコードを読む際には、「C統計量＝C-index」と考えて差し支えありません。

C統計量は0〜1の範囲を取る

C統計量は0から1の範囲で表されます。

• 1.0 → 完全一致（すべてのペアで予測順序が正しい）
• 0.5 → ランダム予測と同等（識別能力がない）
• 0.0 → 完全に逆順（予測がすべて外れている）

実務では、0.7以上であれば「まずまず信頼できる」、0.8を超えると「かなり良いモデル」とされることが多いです。

ただし、これはあくまで目安であり、分野や課題によって基準は変わります。

C統計量とROC曲線・AUCとの違い

ROC曲線（Receiver Operating Characteristic curve）は、分類モデルの性能を視覚的に評価するためのグラフです。

横軸に偽陽性率（False Positive Rate）、縦軸に真陽性率（True Positive Rate）を取り、さまざまな閾値（しきい値）でモデルを動かしたときの点をつなぎます。

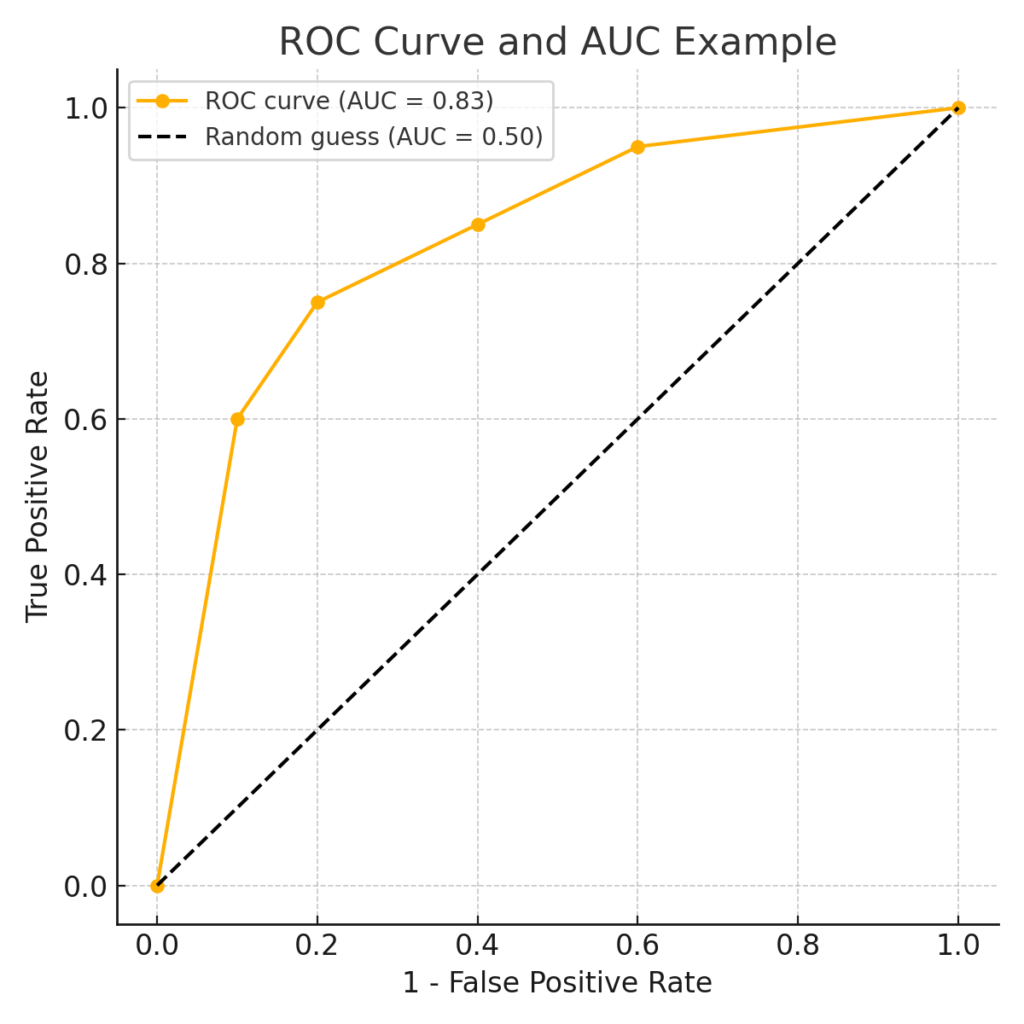
このROC曲線の下の面積を計算したものがAUC（Area Under the Curve）です。

AUCは0〜1の範囲で表され、1に近いほどモデルの識別能力が高いことを意味します。

0.5であれば、モデルがランダム予測と同等であることを示します。

C統計量とAUCの関係

C統計量は、実は二値分類モデルにおいてはAUCと全く同じ値になります。

なぜなら、AUCは「ランダムに選んだ陽性サンプルと陰性サンプルのペアで、モデルが陽性のほうを高く予測できる確率」を表し、これはC統計量の定義と一致するからです。

しかし、C統計量は生存時間解析や順位データにも適用できるという点でAUCより汎用性があります。

特に、生存時間データでは観測が途中で打ち切られる「打ち切り（censoring）」がよく発生しますが、C統計量はこの打ち切りを考慮して計算できます。一方、AUCは通常、二値分類問題に限定されます。

まとめると：

• 二値分類問題 → C統計量 ＝ AUC
• 生存時間解析 → C統計量がAUCの一般化版

C統計量はAUCを包括する概念であり、二値分類では同じになります。

しかし生存時間解析や打ち切りデータを扱う場合にはC統計量が必要になるということです。

C統計量の計算方法

C統計量は、「予測が実際の結果の順序と一致している確率」を求めるだけです。

具体的には、全ての対象ペア（2人組）を比較し、モデルが予測した順序と実際の結果を比べます。

例えば、生存時間解析で患者Aと患者Bを比較したとき：

1. Aの予測リスクがBより低く、かつAが実際に長く生存 → 順序一致（Concordant）
2. Aの予測リスクがBより高いのに、Aが長く生存 → 順序不一致（Discordant）
3. 生存時間が同じ、または予測スコアが同じ → タイ（Tie）

C統計量は、一致ペアの数＋0.5×タイの数 を全ペア数で割ることで求められます。

C統計量の実際の計算式

C統計量の計算式はこのようになります。

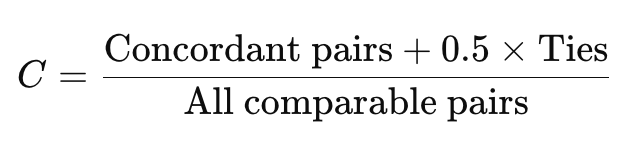
ここで：

• Concordant pairs = 順序が正しいペアの数
• Ties = 同点のペアの数
• All comparable pairs = 比較可能な全ペアの数（打ち切りがある場合は除外）

生存時間解析の場合、打ち切りデータに対しては「比較可能かどうか」を判定し、比較できないペアは計算から除きます。

これが、C統計量がAUCよりも柔軟に使える理由です。

RでC統計量を計算する例

実際にRでもC統計量は簡単に作成できます。

ここでは、Survivalパッケージに含まれる「lung」というデータでC統計量を計算してみます。

# survivalパッケージを読み込み
library(survival)

# lungデータを確認
head(lung)

# Cox比例ハザードモデルを作成
# time = 生存時間（日）
# status = 1: 生存, 2: 死亡 → Surv()内では死亡を1とする必要があるため status-1
cox_model <- coxph(Surv(time, status == 2) ~ age + sex + ph.ecog, data = lung)

# モデルの概要を表示
summary(cox_model)

# C統計量の計算
c_stat <- concordance(cox_model)
c_stat

上記のプログラムを実行すると、C統計量は0.6371と計算することができました。（Concordance=0.6371の部分です。）

C統計量を使うときの注意点

C統計量はペア比較に基づくため、サンプル数が少ないと評価が不安定になりやすいです。

特に、生存時間解析で打ち切りデータが多い場合、比較可能なペア数が極端に減り、C統計量が信頼できない数値になることがあります。

こうした場合は、ブートストラップ法などを使って信頼区間（Confidence Interval）を算出し、不確実性を明示するのが望ましいです。

論文やレポートでも、C統計量単独ではなく「C=0.72（95% CI: 0.68–0.76）」のように提示されるのが一般的です。

また、C統計量は順位の正しさを評価しますが、モデルの絶対的な予測精度やキャリブレーション（予測確率の適切さ）は測れません。

例えば、C統計量が高くても、予測確率そのものが全体的に過大評価されている可能性があります。こうした場合、キャリブレーションプロットなど、別の評価指標も併用すべきです。

まとめ

この記事では、C統計量（C-statistics）とC-indexについて、その意味、計算方法、AUCとの違いまでを解説しました。

ここで改めて、重要なポイントを整理しましょう。

1. C統計量とは？
   • モデルが予測した順位と実際の結果がどれだけ一致しているかを測る指標。
   • 値は0〜1の範囲で、0.5はランダム予測と同等、1に近いほど性能が高い。
2. C統計量とC-indexの関係
   • 中身は同じ指標で、分野によって呼び方が異なるだけ。
   • 医療統計では「C統計量」、機械学習や生存時間解析では「C-index」と呼ばれる傾向。
3. AUCとの違い
   • 二値分類ではC統計量＝AUC。
   • 生存時間解析や打ち切りデータではC統計量がAUCを一般化した形として機能する。
4. 計算方法
   • 全ての比較可能なペアに対して順序が正しいかを判定し、その割合を求める。
   • Rで簡単に計算可能
5. 注意点
   • データの偏りで過大評価の恐れ。
   • サンプル数不足で結果が不安定に。
   • 他の指標と併用することが必須。

---

C統計量は、「モデルが予測の順序をどれだけ正しく当てられるか」を測るシンプルかつ強力な指標です。

特に、生存時間解析やリスク評価のように、単なる的中率では捉えきれない場面で真価を発揮します。

一方で、万能な指標ではありません。

データの質や構造を無視して数値だけを追いかけると、誤った結論にたどり着く危険もあります。

ですから、C統計量を使うときは、必ず他の評価指標や専門知識と組み合わせて判断することを忘れないでください。