医学分野ではCox比例ハザードモデルという解析手法がよく使われます。
生存時間解析で2群の生存率を比較するときに非常に便利な解析なのですが、比例ハザード性というものが成立していないと使えません。
「比例ハザード性って何?」
「どうやって検証するの?」
「比例ハザード性が成立しない場合にはどうすればいいの?」
といった疑問を持つ人も多いのではないでしょうか。
本記事では比例ハザード性とは何か、その検証方法や成立しない場合の対処法について紹介します。
比例ハザード性とは?

そもそも比例ハザード性とは何でしょうか?
紐解いていきましょう!
比例ハザード性の定義
まずは比例ハザード性の定義を調べてみましょう。
共変量の2群間において、ハザード比が時間によらず一定であること。
まだ分かりづらいですよね。
ハザード比とは一体何のことでしょうか?
ハザード比とはそもそも何?
ハザード比とは、2群のハザードの比のことです。
ここで「ハザードって何?」と思いますよね。
まずはハザードとは何か解説していきますね。
ハザードとは、単位時間におけるイベントの発生率を示します。
例えばある薬を使った群と使わなかった群で、数ヶ月の生存率を調べるとしましょう。
この場合、1ヶ月生存できた確率(1ヶ月後の生存者/現時点の生存者)をハザードと表現します。
ちなみにハザードは直訳で”危険”または”障害”という意味になります。
この2群間の生存率の比をハザード比と表現します。
比例ハザード性が成立するのはどんな時?
比例ハザード性とは、2群間のハザード比が時間に限らず常に一定であることです。
比例ハザード性が成立するのはどんな時なのか、先ほどの例を使ってみてみましょう。
以下の場合のカプランマイヤー曲線は比例ハザード性が成立しています。
「薬を使った群が使っていない群よりも常に生存率が1.5倍だった」
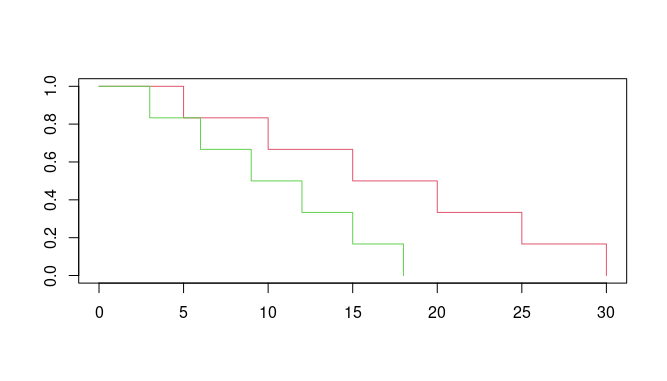
反対に、以下の場合は比例ハザード性が成立していません。
「薬を使った群と使っていない群で、最初は生存率に差がなかったが、12ヶ月後以降は差がみられるようになった」
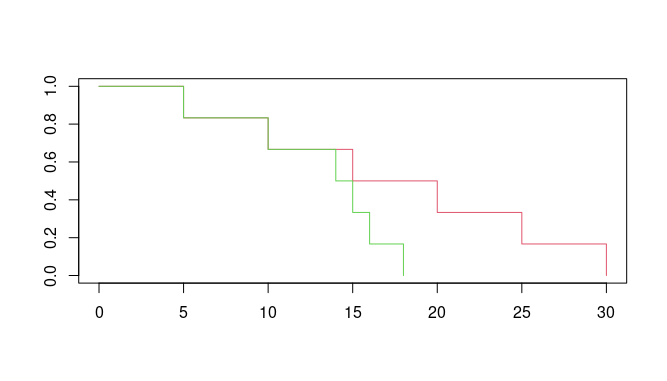
この場合、最初はハザード比が1倍でしたが、12ヶ月以降あたりからハザード比がかなり大きくなっています。
この場合ハザード比は時間によらず一定ではないので、比例ハザード性は成立しません。
このようにデータによって比例ハザード性が成立したり、しなかったりするわけです。
生存曲線の作り方はEZRでカプランマイヤー曲線を作る!という記事をご覧ください。
比例ハザード性の検証方法

実は、比例ハザード性を検証する客観的な方法はまだ確立されていないというのが現状です。
実際に比例ハザード性の検証したい時は、以下の2通りの方法で可能です。
- 生存曲線を目視で確認する
- 層別log-logプロットの平行性を確認する
①生存曲線を目視で確認する
比例ハザード性を検証するなら、ひとまず生存曲線を確認する方法が一番おすすめです。
比例ハザード性が成立するかどうかは、先ほどの例のように生存曲線をみれば大体わかるからです。
生存曲線をグラフ化したときに、2群とも同じような下がり方をしていれば、比例ハザード性は成立していると考えていいでしょう。
反対に、片方の群だけ途中から明らかに下がり方が変わっている場合は、比例ハザード性が成立していないと考えましょう。
この場合そのままCox比例ハザード分析にかけることは出来ませんので、対策が必要です(後ほど解説します)。
②層別log-logプロットの平行性を確認する
①の方法よりももう少しちゃんと比例ハザード性を検証したいときは、層別log-logプロットというものを作り、平行性を確認しましょう。
これは生存時間関数の対数をとった後、符号を反転してもう一度対数をとった関数をプロットしたグラフです。
どうして回りくどい変換をするのは難しい話になるのでここでは割愛します。
ただ、この変換を行うことで比例ハザード性が成立する場合に2つの線が平行になるようになります。
比例ハザード性が成立しない場合は、線が交わったりして平行になりません。
ただこの方法も結局最後は目視での確認ですので、客観性があるとは言い難いです。
基本的には①の生存曲線を目視で確認して大きなズレがなければ比例ハザード性に問題はないと判断してOKでしょう。
比例ハザード性が成立しない場合にはどうすればいい?

比例ハザード性が成立しない変数は、Cox比例ハザードモデルに組み込むことができません。
その場合は、以下の対処法があります。
- 層別Cox比例ハザードモデルを使用する
- 時間依存共変量を取り込む
- 関数に非線形項を追加する
この内②と③は上級者向きですので、統計に詳しくない方は①の方法を検討するのが良いと思います。
層別Cox比例ハザードモデルとは?
層別Cox比例ハザードモデルとは、対象者をある共変量で何層かに分割してCox比例ハザードモデルにかける方法。
先ほどご説明したとおり、比例ハザード性が成立しない変数はモデルに加えられないため、あらかじめ層に分けてしまおうという考え方です。
例を使って考えていきましょう。
例えばある薬を使った群と使っていない群で生存率を調べたいときに、性別を共変量としてCox比例ハザードモデルに組み込みたいとしましょう。
しかし性別と生存率のハザード比が比例しませんでした。
この場合、全体の対象者をあらかじめ男性と女性の2層に分けておきます。
2層を別々に解析することで性別を共変量に組み込まずに解析ができるというわけです。
ちなみに今回は性別を使いましたが、年齢などで何層かに分けることも可能です。
ただしどのように層別化するか決まりはなく、恣意的(都合のいい結果が出るところで層を分ける)に分析ができてしまうという欠点があります。
層別Cox比例ハザードモデルを使う時は先行研究を参考にして、なるべくオーソドックスな分け方をするようにしましょう。
②と③については詳しい説明を省きますが、いずれも時間に比例しない変数を加える方法です。
②はそんな都合の良い変数を見つけなければなりませんし、③は作り出さなければなりません。
どちらも数学的な知識がないと失敗しやすい方法です。
たいていは層別モデルで対応できるため、初心者のうちは①の方法をおすすめします。
まとめ

最後におさらいをしましょう。
- 比例ハザード性とは時間に関係なくハザード比が一定であること
- 生存曲線をプロット(グラフ化)することで比例ハザード性を確認できる
- 比例ハザード性を確かめる客観的指標は確立されていない
- 比例ハザード性が成立しない場合は層別Cox比例ハザードモデルを使用する
Cox比例ハザード分析を使用した論文は多くありますが、比例ハザード性の検討を怠っている方は案外多いように感じています。
間違った結果を発表しないためにも、注意する癖をつけておきたいですね。
今回は比例ハザード性について解説させて頂きましたが、生存曲線解析について解説した記事がこちらにもありますので、よければ一緒にご覧ください。
最後までお読み頂きありがとうございました。












コメント