重回帰分析での寄与率（R2）とrの関係は？補正された決定係数の意味

この記事では「重回帰分析での寄与率（R2）とrの関係は？補正された決定係数の意味」ということでお伝えします。

• 単回帰分析の場合のR2と相関係数rとの関係は？
• 重回帰分析の場合のR2と相関係数rとの関係は？
• 重回帰分析の場合R2とAdjusted R2のどちらを使うの？

ということが理解できるような内容ですので、ぜひ最後までご覧ください！

 

単回帰分析の場合のR2と相関係数rとの関係は？

重回帰分析について解説する前に、単回帰分析での寄与率（R2）や相関係数rについて整理しておきましょう。

単回帰分析とは、説明変数が一つしかない場合の回帰分析のこと。

今回の記事では特に、目的変数も説明変数も連続量である場合を考えてみます。

 

単回帰分析での相関係数と回帰分析

単回帰分析を実施すると、

1. 散布図
2. 相関係数
3. 回帰分析

の3つの解析ができます。

例えば、架空のデータをEZRで2つの連続変数に対する相関係数の分析を実施すると、以下の通り散布図と回帰直線と相関係数が出力されます。

↓散布図と回帰直線

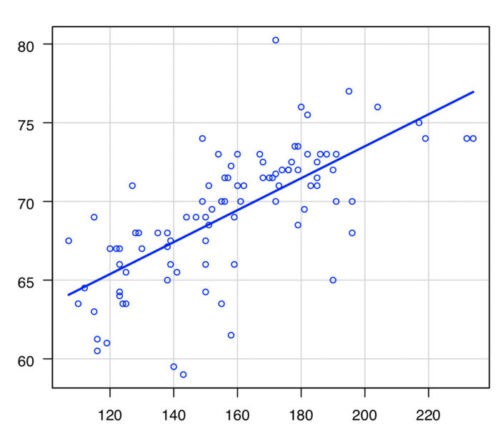
↓相関係数（ピアソンの相関係数）

そして同じデータに対してEZRで回帰分析を実施すると、寄与率（決定係数、R2値）が出力されます。

Multiple R-squared：0.4802が寄与率（決定係数、R2値）です。

 

R2と相関係数rとの関係は？

数値として出力されたのは

• ピアソンの相関係数r：0.693
• 単回帰分析の寄与率：0.4802

です。

この時、寄与率（決定係数、R2値）と相関係数rとの関係はどうなっているでしょうか？

実は、相関係数rを2乗した結果が寄与率（決定係数、R2値）になっています。

（逆に言えば、寄与率のルートが相関係数になります。）

実際に0.693*0.693を計算してみると、0.4802になることがわかります。

 

重回帰分析の場合のR2と相関係数rとの関係は？

単回帰分析での寄与率（決定係数、R2値）と相関係数rとの関係がわかったところで、重回帰分析での話をしていきましょう。

まず重回帰分析の復習。

重回帰分析とは、説明変数が2つ以上の場合の回帰分析のことを言います。

単回帰分析では散布図という図式化ができましたが、重回帰分析の場合、目的変数と合わせて3次元以上の解析になるので図式化は難しいです。

そのため、重回帰分析では主に数値による評価が必要です。

 

重回帰分析の寄与率（R2）は何を示しているのか？

重回帰分析の寄与率（R2値）は、単回帰分析のR2値の拡張版。

目的変数の全変動(yの平方和)のうち、説明変数全体によって説明される割合を意味します。

つまり、説明変数だけで目的変数を何%説明できるか？という指標です。

例えば寄与率（R2値）が0.4である場合、回帰分析に含めている説明変数で、目的変数を40%説明できている、ということ。

説明できない残りの60%が、誤差ということです。

 

重回帰分析のR2の平方根（ルート）であるRは何を意味する？

単回帰分析の場合、寄与率のルートが相関係数でした。

では重回帰分析の重回帰分析のR2の平方根であるRは何を意味するでしょうか？

結論から言うと、Rは重相関係数(multiple correlation coefficient)という値。

重回帰式による予測値と実際に測定される値との相関関係の程度を示す数値です。

 

実際にEZRでやってみた数値を見ながら解説してみます。

「体重＝身長+年齢」という、目的変数が体重、説明変数が身長と年齢の2つを考えます。

架空のデータで重回帰分析をすると、寄与率（R2値）が出力されます。

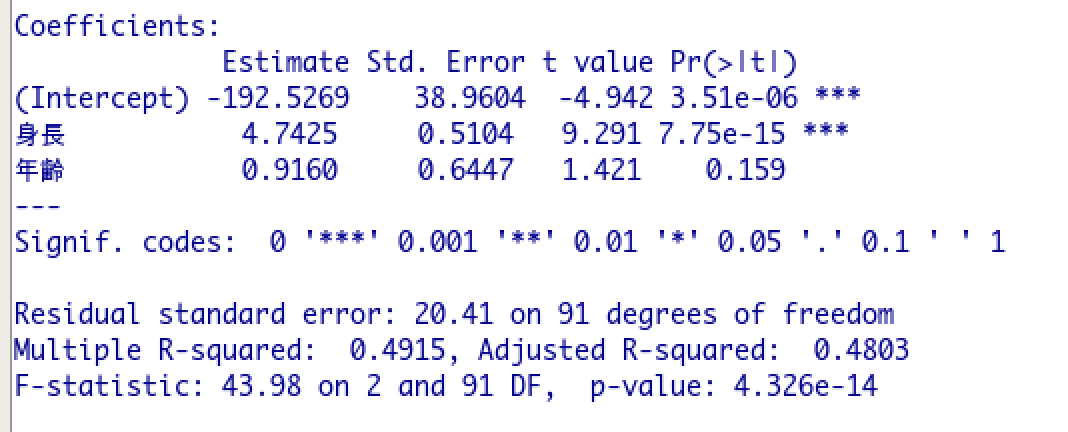
Multiple R-squared：0.4915が寄与率（決定係数、R2値）です。

この時、身長の偏回帰係数4.7425と、年齢の偏回帰係数0.9160を用いて、各データの予測値を計算することができます。

そして計算した体重の予測値と、体重の実測値でピアソンの相関係数を算出すると以下の結果が出力されます。

0.701*0.701を計算すると0.4914ですから、Multiple R-squared：0.4915に一致します。

 

重回帰分析の場合R2とAdjusted R2のどちらを使うの？

ここまでで

• 単回帰分析の場合のR2と相関係数rとの関係
• 重回帰分析の場合のR2と相関係数rとの関係

の2つを整理できましたね。

最後、重回帰分析で重要な知識である、「R2とAdjusted R2のどちらを使うのか？」について解説します。

再度、重回帰分析の結果を見てみます。

すると、Multiple R-squaredとAdjusted R-squaredの2つが出力されていることがわかります。

Multiple R-squaredが補正なしのR2値、Adjusted R-squaredは補正されたR2値です。

両者はどう違うのでしょうか？

 

重回帰分析のR2（補正なし）は何を意味するのか？

補正なしのR2値は、既に解説した通りです。

つまり、単回帰分析のR2値の拡張版であり、目的変数の全変動(yの平方和)のうち、説明変数全体によって説明される割合を意味します。

ここで悩ましい特徴があって、それは「説明変数を入れれば入れるほど値が必ず大きくなる」という特徴。

この特徴があることで、「無理矢理説明変数を入れればいいのでは？」というアイデアになってしまう問題が出てきます。

その問題に対処するのが補正したR2値です。

 

重回帰分析の補正されたR2は何を意味するのか？

補正されたR2値は、説明変数の数でペナルティを与えたR2値です。

つまり、説明変数を増やしたとしてもペナルティよりも寄与率R2の増え方が大きくないと意味がないため、上記の「説明変数を入れれば入れるほど値が必ず大きくなる」という特徴がなくなります。

そのため、本当に必要な説明変数を選択しなければなりませんし、そのことによって適切なモデルを選択することができます。

重回帰分析をする場合、補正されたR2値を常に使うことをお勧めします。

 

ただし、補正されたR2は平方根をとっても重相関係数にはならないので、そこだけは解釈が難しいということだけ頭の片隅に入れておいてください。

 

まとめ

いかがでしたか？

この記事では「重回帰分析での寄与率（R2）とrの関係は？補正された決定係数の意味」ということでお伝えしました。

• 単回帰分析の場合のR2と相関係数rとの関係は？
• 重回帰分析の場合のR2と相関係数rとの関係は？
• 重回帰分析の場合R2とAdjusted R2のどちらを使うの？

ということが理解できたのなら幸いです！

 

こちらの内容は動画でも解説していますので、合わせてご覧くださいませ。