この記事では、偏回帰係数について詳しくお伝えします。
- 偏回帰係数とは？回帰係数との違いは？
- 偏回帰係数の有意性はどう判断する？
- 偏回帰係数がマイナスになってしまった時はどうすればいい？
といった疑問についてお答えしていきます！
重回帰分析を解釈する上で重要な偏回帰係数。
共分散分析やロジスティック回帰分析、Cox比例ハザードモデルの解釈にも重要な知識ですので、是非マスターしましょう！
偏回帰係数とは？どんな意味を持つの？
偏回帰係数は、回帰分析の中でも重回帰分析という複数の独立変数を用いて従属変数を表す回帰分析において、回帰式の中に現れる傾きを表す係数のことです。
重みとも呼ばれ、幾何学的には直線の傾きに相当する。
偏回帰係数という言葉における「偏」という意味は、他の独立変数の影響を除外した場合のその変数の重みという意味で用いられます。
偏回帰係数とは重回帰分析での独立変数の係数のこと
重回帰分析では、複数個の独立変数と従属変数の間に次のような一次式の関係があるとします。
従属変数＝偏回帰係数1×独立変数1＋偏回帰係数2×独立変数2＋・・・＋偏回帰係数n×独立変数n＋定数項＋誤差項
ここで、定数項の部分を回帰定数、各独立変数の係数を偏回帰係数と呼ぶ。
例えば、身長、腹囲、胸囲、太ももの太さという独立変数から体重という従属変数を予測し、説明する場合、次のような一次式が得られるとする。
体重＝偏回帰係数1×身長＋偏回帰係数2×腹囲＋偏回帰係数3×胸囲＋偏回帰係数4×太ももの太さ＋20＋誤差項
ただし、誤差項については、
- 不偏性：各誤差項の平均は0
- 等分散性：各誤差項の分散はシグマの２乗
- 無相関性：各誤差項の共分散は0
- 正規性：各誤差項は、平均が0、分散がシグマの２乗の正規分布に従う
という仮定を満たすとする。
偏回帰係数と回帰係数の違いは？
重回帰分析の目的は、従属変数を複数の独立変数を用いて予測、説明することです。
独立変数の予測力、説明力とは、従属変数に対する独立変数の影響の大きさと考えることができます。
そのために、最小二乗法を用いて、従属変数の実測値と予測値との誤差の２乗和が最小になるような回帰定数と偏回帰係数を求める。
その際に、独立変数相互の相関関係についても考慮し、その影響を取り除いて、各独立変数の従属変数に対する影響を純粋な形で取り出そうとする。
独立変数同士の影響を取り除いて従属変数に対する影響度合いを示しているため、重回帰分析ではその回帰係数を「偏回帰係数」と呼んでいるのです。
一方、単回帰分析では、従属変数を1つの独立変数を用いて予測・説明すること。
つまり、独立変数は1つしかないため、独立変数同士の影響を考える必要がない。
そのため単回帰分析での回帰係数は、単に「回帰係数」と呼びます。
しかし、実際には偏回帰係数と回帰係数の違いを意識して用語を使っている人は少なく、どの場合であっても「回帰係数」と呼ぶことが多いですね。
偏回帰係数の理解を深める事例1
では、具体的な事例を用いて偏回帰係数の理解を深めましょう。
以下では、マンション価格Ｙを最寄り駅までの徒歩による時間X1、広さX2および築年数X3で重回帰分析をします。
事例1
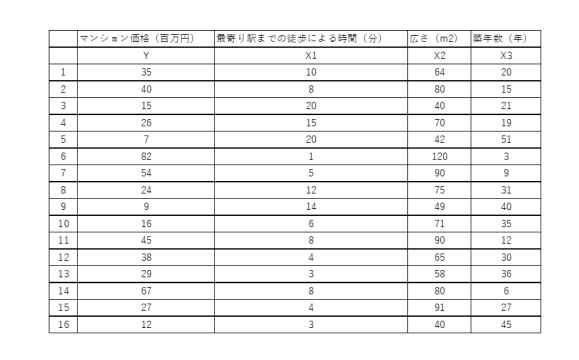
マイクロソフトのエクセルの機能を用いて、実際に重回帰分析を行った結果が以下の表のようになります。
重回帰分析結果1
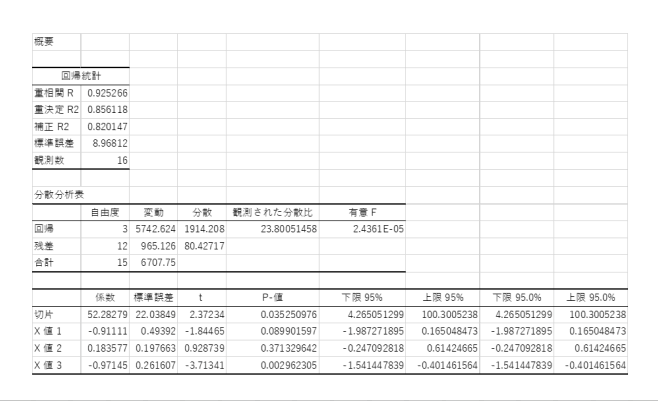
偏回帰係数1＝－0.91111、偏回帰係数2＝0.183577、偏回帰係数3＝－0.97145となった。
この結果、Ｙ＝52.28279－0.91111X1＋0.183577X2－0.97145X3となる。
偏回帰係数の検定結果の解釈はどうすればいい？
偏回帰係数の有意性はt検定の結果を解釈
偏回帰係数の検定にはt検定が使われる。
帰無仮説と対立仮説は以下の通りです。
- 帰無仮説：偏回帰係数1=偏回帰係数2= ・・・ =偏回帰係数k=0
- 対立仮説：偏回帰係数1、偏回帰係数2、・・・、偏回帰係数kのうち少なくとも1つは0ではない
としてT検定を行い、帰無仮説が棄却されれば、偏回帰係数1、偏回帰係数2、・・・、 偏回帰係数kのうち少なくとも1つは0ではない、つまり、独立変数のうち少なくとも1つは従属変数のモデル化に貢献していると判断する。
このとき、t値の大きさは、その独立変数の従属変数に対する説明力の高さを表すものと考えられます。
言い換えると、t値の大きな独立変数ほど、従属変数をよく説明できているということ。
このt検定はある独立変数以外の独立変数が全て存在することを前提とした上で、この独立変数が従属変数の説明力向上に貢献するか否かを判断するもので、この前提が妥当でなければ、検定の結果も妥当と解釈はできません。
したがって、重回帰分析では独立変数の選択自体が重要な問題となる。
また、通常の重回帰分析では独立変数間に相関がある場合が多く、それらが有機的に組み合わさって従属変数に影響を与えていると考えられます。
したがって、個々の独立変数を独立に検定することにはあまり意味がなく、特定の独立変数の組み合わせが従属変数にどの程度影響しているかを評価することの方が重要。
すなわち、どのような独立変数を組み合わせたモデルが最適かを評価することが重要ということ。
ところで、p値は帰無仮説「偏回帰係数1=偏回帰係数2= ・・・ =偏回帰係数k=0」を仮定したとき、今回のt値はどれくらいあり得ないかという確率を表しています。
上の事例1では、X1のp値＝0.08990、X2のp値＝0.37133、X3のp値＝0.00296ですから有意水準0.05より小さいものは、X3でこれは有意、X1とX2は有意でないという結論になる。
偏回帰係数がマイナスな時の解釈は？
偏回帰係数がマイナスな時は、多重線形性の可能性を疑う必要があるかも
偏回帰係数がマイナスになった場合、どのように解釈したらいいでしょうか。
偏回帰係数がマイナスになったからといって直ちに重回帰分析がおかしいということはありません。
合理的に考えてマイナスになるべきであれば間違っていないからです。
事例1でいうと、最寄り駅までの徒歩による時間X1と築年数X3がマイナスですが、最寄り駅までの徒歩による時間と築年数が小さければ小さいほどマンション価格高くなるのは常識的に正しいのでこれはいい。
ところが、本来偏回帰係数がプラスになると想定していたのにマイナスになった場合は、多重線形性が原因でないかどうか検討する必要がある。
重回帰分析において、独立変数どうしの相関係数が±1に近い組合せが含まれる場合に係数の推定値の分散が大きくなり、その結果係数の推定値が不安定になることがある。
このような現象のことを多重線形性といいます。
多重線形性が起こると重回帰分析のモデル推定の際に以下のような問題が生じてしまいます。
- パラメータの推定値が真の値と大きく異なってしまう（極端な場合、符号が逆になる）
- 明らかに有力な独立変数が検定によって有意にならない
- 決定係数（独立変数の予測値の分散を独立変数の標本値の分散で割ったもの）が高いにもかかわらず各変数の有意性が低い
ですから、これらの問題を避けるために、重回帰分析を行う前にまず、各独立変数間に相関関係がないかどうかを検討する必要があるのです。
多重共線性が生じると、偏回帰係数を解釈すること自体が無意味ということになりかねない。
多重線形性に対する対処方法としては、独立でないいくつかの独立変数を取り出し、先行研究の知見や専門的な知識、経験を総動員して、遂行しようとしている研究に対して重要だと考えられる独立変数のみを残すという方法があります。
このようにして、多重線形性が原因で偏回帰係数がマイナスになったものを排除したあとに偏回帰係数がマイナスになったものがあるとすればそれは、従属変数と独立変数はそもそも負相関であることが妥当であると解釈する。
まとめ
重回帰分析の中で偏回帰係数は重要な意味を持つ
偏回帰係数の意味が理解できたでしょうか。
偏回帰係数とは、ある独立変数から他の独立変数の影響を除いた残差変数によって従属変数を予測するときの回帰係数のことで、独立変数と従属変数との相関係数（単相関）ではありません。
単純な２変数間の相関関係ではなく、条件つきの相関関係なのです。
ある独立変数が動くことで一般的にはそれにともなって他の独立変数も動くが、仮にそれがまったくないとした場合のある独立変数の効果という意味を偏回帰係数は持つ。
重回帰分析の目的の１つは、独立変数のうちどれが一番従属変数をよく説明していかを知るということですが、このような意味を持つ偏回帰係数が重要となる理由はまさに偏回帰係数自体が持つこの意味にあるといえるのです。
第1章：医学論文の書き方。絶対にやってはいけないことと絶対にやった方がいいこと
第2章：先行研究をレビューし、研究の計画を立てる
第3章：どんな研究をするか決める
第4章：研究ではどんなデータを取得すればいいの？
第5章：取得したデータに最適な解析手法の決め方
第6章：実際に統計解析ソフトで解析する方法
第7章：解析の結果を解釈する
もしあなたがこれまでに、何とか統計をマスターしようと散々苦労し、何冊もの統計の本を読み、セミナーに参加してみたのに、それでも統計が苦手なら…
私からプレゼントする内容は、あなたがずっと待ちわびていたものです。
[…] これは、（偏）回帰係数の仮説検定を通して確認されます。 […]
[…] 予測値とは、回帰分析で算出された偏回帰係数を使い、回帰式に準じて計算された値のことです。 […]