本記事では「回帰分析での予測値の求め方は?残差を使って比較する方法も解説」ということでお伝えしていきます。
回帰分析をしていると、実測値・予測値・残差という用語が出てきて「どれがどんな意味を持つの?」ということが疑問になったりしますよね。。
そこで
- 実測値・予測値・残差の3つの用語を整理
- 予測値と残差の求め方をEZRで実践
- 予測値と実測値の比較方法
を解説してきますね!
回帰分析における予測値・実測値・残差とは?

まずは、実測値・予測値・残差の3つの用語を整理しておきましょう。
実測値とは、実際に測定して得られてた実データのことです。
「体重の実測値」と言われたら、実際に体重計に乗って測定したデータのことですね。
予測値とは、回帰分析で算出された偏回帰係数を使い、回帰式に準じて計算された値のことです。
回帰分析で計算された通りのデータだとするとこんな感じ、という理論値。
例えば「体重の予測値」と言われたら、目的変数を体重として説明変数を身長と年齢のにしたとき、身長と年齢の実測値と偏回帰係数から求められる体重の値のことです。
説明変数が変われば回帰式も変わるため、体重の予測値は変わります。
残差とは、実測値と予測値の差のこと。
残差が小さければ、予測値と実測値との乖離が小さいので、精度の良い回帰分析ができているということになります。
予測値と残差の求め方をEZRを使って解説

用語が整理できたところで、実際に架空のデータを使って予測値の求め方を解説していきます。
今回、「体重=身長+年齢」という説明変数が2つの回帰分析を考えます。
それぞれの単位は「体重:kg、身長:インチ、年齢:歳」です。
EZRで予測値の求め方1:まずは回帰分析を実施する
予測値を求めるには、まず回帰分析を実施する必要があります。
というのも、予測値には「偏回帰係数」が必要だからです。
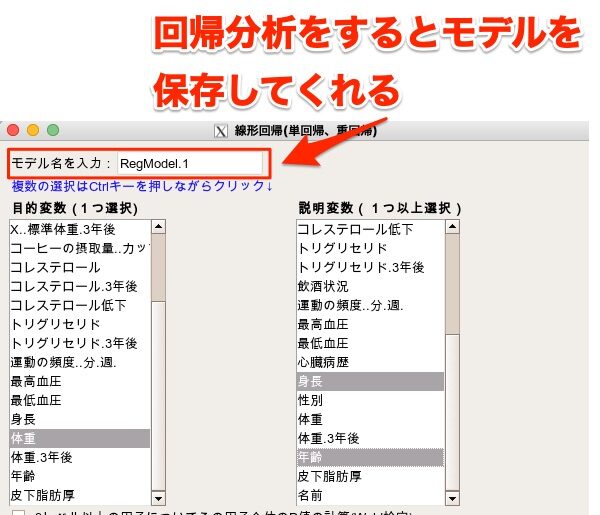
EZRではデータを読み込んだ後、以下の画面で回帰分析ができます。
「統計解析」>「連続変数の解析」>「線形回帰(単回帰、重回帰)」
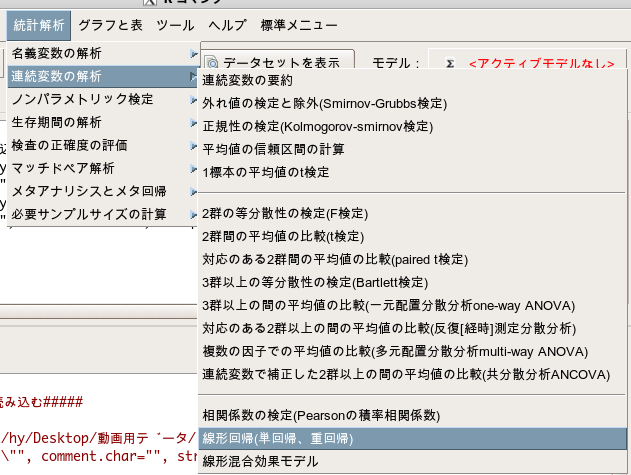
目的変数に「体重」を選択し、説明変数に「身長」と「年齢」を選択します。
これでOKを押すと、重回帰分析の結果を出してくれます。
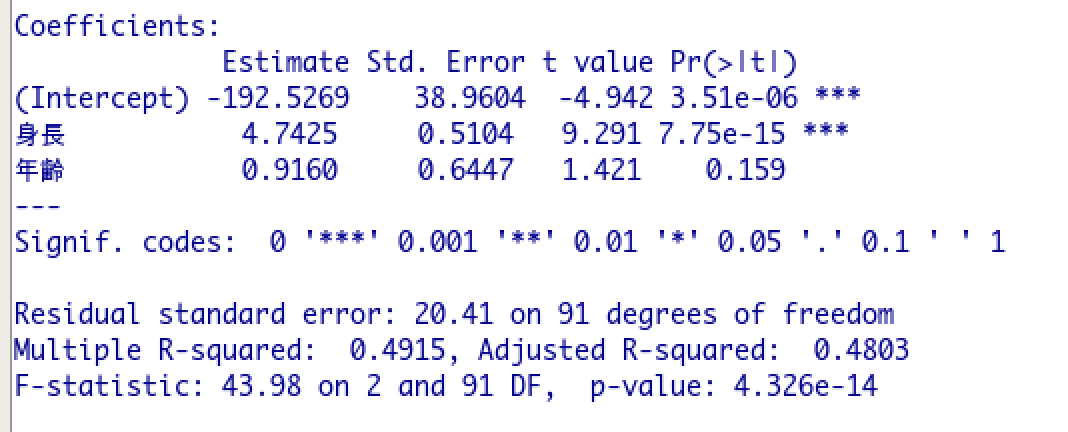
これで、偏回帰係数が得られました。
つまり今回の回帰分析では以下の回帰式が得られたということです。
体重の予測値=4.7425*身長+0.9160*年齢-192.5269
この回帰式を元にすると、仮に身長が70インチ、年齢が30歳の人であれば
4.7425*70+0.9160*30-192.5269=166.9kg
という体重の予測値が得られる、ということになります。
EZRで予測値の求め方2:予測値と残差をデータセットに保存する
回帰分析をした結果から、予測値をデータセットに保存する方法をお伝えします。
まず、右上の「モデル」と書かれてある部分は「アクティブモデルなし」になっているかと思います。
この「アクティブモデルなし」の部分をクリックすると、「モデルの選択」をすることができます。
先程の回帰分析をした際のモデルをクリックします。
「回帰分析をした際のモデルって??」と思うかもしれませんが、重回帰分析をした際に、EZRでは勝手にモデルを保存してくれます。
モデルを選択すると「モデル」の部分が変わります。
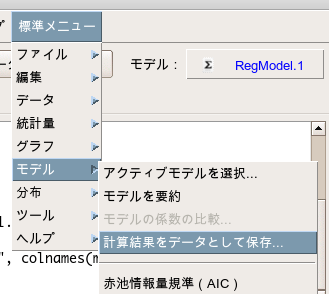
この状態になったら、「標準メニュー」>「モデル」>「計算結果をデータとして保存」を押します。
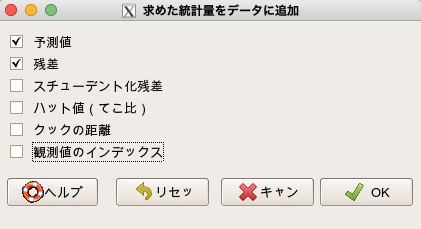
すると、どの計算結果を保存するかを選択できますので、「予測値」と「残差」を選択してOKを押します。
その後データセットを開くと、予測値(fitted〜〜)と残差(residuals〜〜)が保存されていることがわかります。
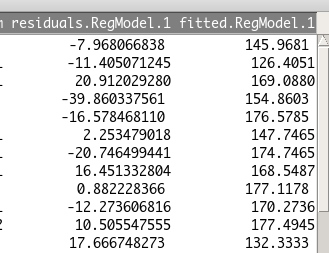
以上で、EZRで予測値と残差を求めることができました。
予測値と実測値を比較する方法は?

予測値や残差を求めることができましたね。
次に疑問になるのが「予測値を求めてどう使うの?」ということです。
予測値はあくまで「得られた回帰式からの理論式」なので、実測値との乖離度合いがどれぐらいか?という情報が重要そうですよね。
なので、予測値と実測値を比較してみることが重要です。
予測値と実測値の比較1:予測値と残差でプロットする
残差=実測値-予測値ですから、残差を見ることで実測値と予測値の乖離度合いを見ることができそうですよね。
残差の定義を見ると、正の値の残差(Y軸)は予測が低いことを示し、負の値は予測が高いことを示し、0の値は予測が正しい、ということが言えそうです。
そこで、予測値をX軸に取り、残差をY軸に取った残差プロットを作成してみます。
(下記のグラフのY軸:残差は標準化しています)
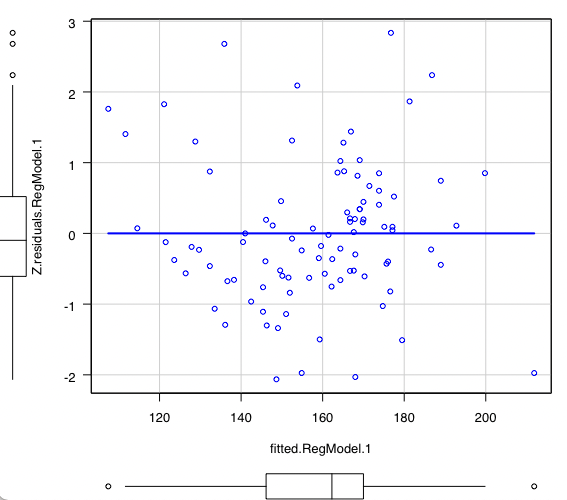
このプロットからどんなことを読み取るのかというと、
- 分布が対称的で、プロットの中央にデータが多いかどうか
- 残差を標準化した場合、Y軸の±2の範囲にデータが多く集まっているかどうか
- それ以外に明確なパターンがない
ということがざっくり読み取れればOKです。
上記のグラフはまぁまぁいい感じ、ということです。
予測値と実測値の比較2:重相関係数を出してみる
アイデアの2つ目は、重相関係数を算出してみる、ということです。
重相関係数とは、重回帰式による予測値と実際に測定される値(実測値)との相関関係の程度を示す数値。
1に近いほど分析の精度(予測値の精度)は高いです。
そこで、予測値と実測値でピアソンの相関係数を算出みると、以下の結果になりました。

一般的に相関係数が0.7はかなりいいので、トータル的に良い予測ができているのでは、と解釈できます。
ちなみに、重相関係数の2乗が、重回帰分析の寄与率(R2値)と呼ばれているものです。
まとめ

いかがでしたか?
本記事では「回帰分析での予測値の求め方は?残差を使って比較する方法も解説」ということでお伝えしました。
- 実測値・予測値・残差の3つの用語を整理
- 予測値と残差の求め方をEZRで実践
- 予測値と実測値の比較方法
が理解できたのなら幸いです^^













コメント