回帰分析とは？p値や回帰係数の意味も例題で簡単にわかりやすく！

「回帰分析」という解析手法を知っていますか？

「回帰分析」という名前を聞くと何となく「難しそう」と思ってしまいますが、実は簡単なんです！

回帰分析がどれぐらい簡単かというと、中学校で学んだ「y=ax+b」が分かれば、理解できます！

ということで、この記事では回帰分析について例題を用いながらわかりやすく簡単に解説します！

具体的には

• 回帰分析とは何をやっているの？
• 回帰分析で出てくる回帰係数とは？
• 回帰係数のP値や有意の意味とは？

といったことをお伝えしますね。

 

回帰分析は２種類以上のデータがあった時にやる解析

２種類以上のデータがあった時。

あなたはどんな解析をしますか？

例えば、体重と身長のデータがあった時。

 

どんな解析をしたとしても、特に正解や不正解があるわけではありません。

私がやるとしたら、こんな解析をしてみます。

 

 

最初にやっぱりそれぞれのデータがどうなっているか確認しますね。

そして、より複雑な解析に移動していく。

このページでは、私の中で最後に実施する、回帰分析の話をします。

 

回帰分析とは何をやっているか例を用いてわかりやすく

回帰分析ってよく聞くけど、何をやっているのかわからない。。

あなたもそんな1人かもしれません。

中学校で必ず学ぶこの方程式。

 

懐かしいなーと思う方が多いと思います。

中学校では、こんな問題が出ますよね。

「(2,8),(4,14)の２点を通る直線y=ax+bのaとbを求めよ」

この時に、連立方程式を解いて、a=3, b=2という答えを導き出しました。

 

回帰分析でやっていることは、これと同じです。

まずは、回帰分析の式を見てみます。

式は、以下の通りです。

中学校で習った方程式と一緒じゃないですか？

唯一違うのが、最後に「誤差」がある点。

 

回帰分析の最後の誤差は何者？

回帰分析で特徴的な最後の誤差。

これがあることで、一気に難しくなった感じがしますよね。

でも、何のことはないです。

 

統計の基礎を思い出してください。

データはばらつきます。

このばらつきを、最後の誤差で表現しているにすぎません。

 

回帰分析の誤差を例を用いて概要を理解してみる

例えば、身長が170センチの男性。

この男性の体重を知りたいとします。

でも、同じ170センチだったとしても、体重は50kgの人がいたり、100kgの人がいたりしますよね。

つまり、以下のような方程式を作った場合。

Y（体重）=ax（身長）+b+誤差

Xに170を入れたとしても、Yが50だったり100だったりします。

 

つまり、aとbが決まったとしても、170センチの身長の人が全員同じ体重になりませんよね。

統計用語で言えば、バラつきがあるということ。

そのバラつきを、最後の「誤差」で表現しているのです。

全てのデータが一直線上に乗るようなデータであれば誤差は０なので、中学校で習った方程式と一緒になります。

でも、現実世界のデータでそのような一直線になる関係は絶対にありえないのです。

そのため、最後に「誤差」があるのです。

 

回帰分析では回帰係数のaとbをどうやって決めるか？

全てのデータが完全に直線上に乗るのであれば、aとbはすぐに決まりました。

でも、バラついたデータでは、aとbは簡単には決められないのです。

なぜなら、データに対して様々な直線を引く選択肢が出てくるからです。

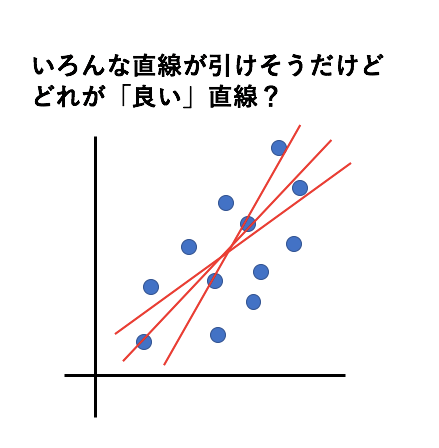
この無数の選択肢がありそうな直線の中から、「良い」直線を選ぶ方法が必要になります。

あなたならどういった直線が「良い」直線と思うでしょうか？

統計の世界では、「良い」直線を決めるための方法の１つに最小二乗法という方法を採用しています。

もしかしたら、聞いたことがあるかもしれませんね。

最小二乗法は何をやっているのかというと、以下の３つです。

 

 

専門用語を使って、この1-3を表現すると以下のようになります。

 

 

最も小さい偏差平方（二乗）和を求めるので、最小二乗法と言います。

 

回帰分析に関して用語の整理

今後の説明がスムーズになるように、回帰分析で出てくる用語を整理しておきます。

 

 

これだけ覚えておけば、他の教科書を見てもスムーズに理解できると思います。

特に、目的変数と説明変数は混同している方が多かったりしますので、ぜひ正確に覚えておきましょう。

 

単回帰分析と重回帰分析の違いは？

ちなみに、説明変数が一つの場合に「単回帰分析」と言います。

説明変数が２つ以上の場合に「重回帰分析」と言います。

Y（体重）＝a*x（身長）+b+誤差

は単回帰分析。

Y（体重）＝a*x1（身長）+c*x2（年齢）+b+誤差

は重回帰分析です。

 

回帰分析の解析結果の例からp値や有意の意味を理解する

理論的なことはこれだけなのですが、実際の解析結果の例を見ながら、さらに理解していきましょう。

回帰分析ではp値が出てきますが、その意味は？というのも解説します。

 

例えば、統計検定２級の２０１８年６月の問題から。

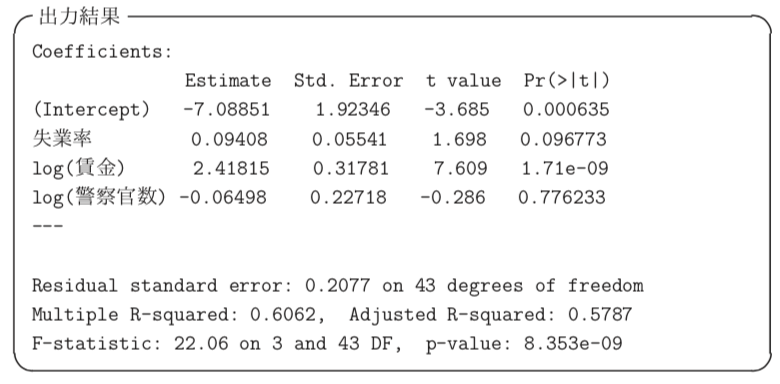
このような出力結果があった時の、結果の解釈を理解してみましょう。

 

回帰分析では回帰式を思い浮かべる

このような出力結果が出てきた時に、真っ先に以下のような回帰式を思い浮かべてください。

 

 

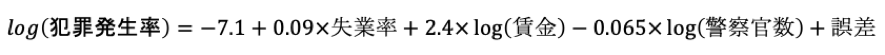
回帰式の定義をもう一度復習しておきます。

Y=ax+b+誤差

これに、当てはめただけなので、そんなに難しいことはないはずです。

 

回帰分析のp値や有意の解釈は？帰無仮説を確認する！

この出力結果にp値が出ていますよね。（Pr > (|t|)の部分）

悩ましいのが、この解釈かなと思います。

 

p値が出てきた時、当然、何かの統計学的な検定をしているはずです。

検定が出てきたら気にすべきこと。

ありましたよね。

そうです、帰無仮説と対立仮説を確認することです。

回帰分析での帰無仮説と対立仮説もあるんです。

 

帰無仮説：回帰係数＝０

対立仮説：回帰係数≠０

 

これが帰無仮説と対立仮説です。

で、p値が0.05を下回ったら有意差がある。

つまり、解釈としてはこうなります。

 

回帰係数のp値が0.05を下回った場合、有意差がある。

つまり、その回帰係数が０であるという帰無仮説を棄却する。

 

これがp値が0.05を下回った場合の解釈です。

 

回帰係数が０である、ってどういうこと？

p値が0.05を下回れば、回帰係数が０ではない、ということが言えました。

重要なのが、その意味です。

意味を解釈するには、まずは回帰係数が０である、ということを理解する必要があります。

回帰係数が０って、どう意味かわかりますか？

 

回帰係数が０の場合、その変数（Xの値）がどのような値を取ろうとも、Yには全く影響を与えませんよね。

例えば、「体重=０×身長＋５０＋誤差」という式があった時。

変数である「身長」の回帰係数が０です。

この時、身長が１５０センチだろうが、２００センチだろうが、体重は変わりません。

だって、回帰係数が０だから。

体重（Y）に対して、身長（X）が全く影響を与えない。

 

ここが重要なのです。

長々と書いてしまったので、簡潔にまとめます。

 

回帰係数が０の場合、その変数（X）は応答変数（Y）に影響の与えない因子である。

逆に、回帰係数が０ではない時には、その変数（X）は応答変数（Y）に影響の与える因子である。

 

この解釈を、ぜひ理解してください。

 

 

回帰分析から、共分散分析へ

回帰分析を学ぶことで、XとYの関係を知ることができます。

また、p値の解釈ができると、その結果の見方がかなり変わります。

ぜひ、なんども読んで理解してみてくださいね。

 

そして、回帰分析を理解することは、共分散分析を理解することにつながります。

医薬統計をやっていると、共分散分析は絶対に避けては通れないので、ぜひその意味でも回帰分析をちゃんと理解しましょう。

また、ロジスティック回帰やCox比例ハザードモデルなんかも、この回帰分析の知識の上に成り立っています。

 

回帰分析に関してまとめ

回帰分析とは、中学校で学んだ「Y=ax+b」という式と同じ。

上記の式に誤差を含んだもの。

aとbを求めるために、最小二乗法という方法を用いている。

回帰分析を学ぶことで、共分散分析を理解することができる。