多変量解析でモデル選択・変数選択をする際に、クロスバリデーション(交差検証)が必要になることがあります。
得られているデータを全て使って一度だけモデルを構築して終わり、という方法だと過学習（オーバーフィッティング）の問題が出てくるため、過学習を回避するのにクロスバリデーションを実施することが多いですね。
でもクロスバリデーションについて知らないという方も多いのではないでは？
本記事では、クロスバリデーションの意味や行う理由、具体的な使用の流れなどを解説していきます。
初心者にも分かるよう解説していきますので、クロスバリデーションについて詳しくなっていって下さいね！
クロスバリデーションはモデル選択・変数選択でなぜ必要？その意味と実施する理由は？
まずはクロスバリデーション自体について学んでいきましょう！
クロスバリデーションとは？
クロスバリデーションとは、作成した予測モデルの性能(精度)を検証することです。
例えばロジスティック回帰分析でどんな変数を組み合わせるのが1番いいのか、というモデル選択（変数選択）を実施しますよね。
モデル選択の一つの方法がステップワイズ法でした。
でもそのモデルが本当に適切かどうかを判断する必要があります。
それが、モデルの性能を検証するということ。
どのように性能の検証を行うのか簡単に説明していきますね。
機械学習モデルを作る時は、予測モデルを作るためのデータが必要です。
このデータを使って予測モデルを作っていくわけですが、クロスバリデーションを行う場合はこのデータを学習データとテストデータに分割します。
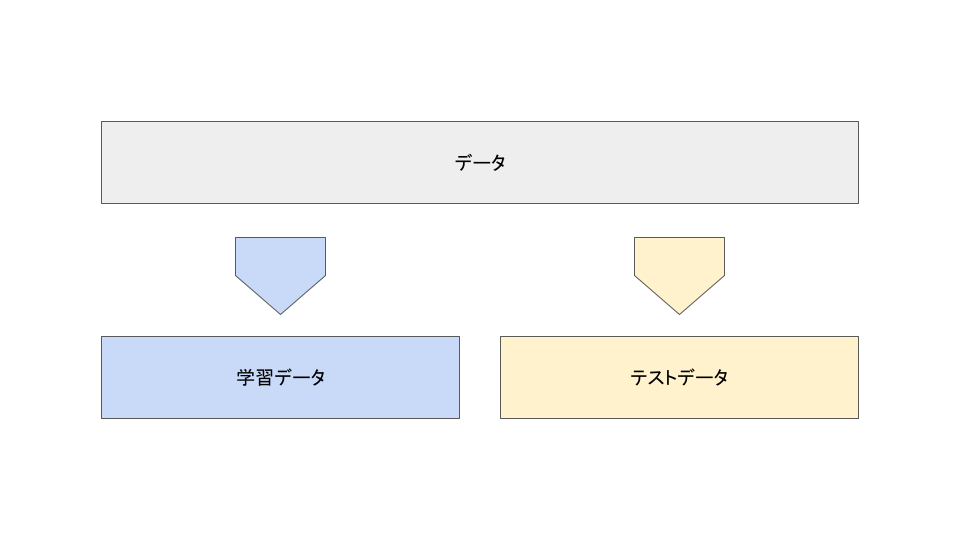
学習データは予測モデルを作るためのデータです。
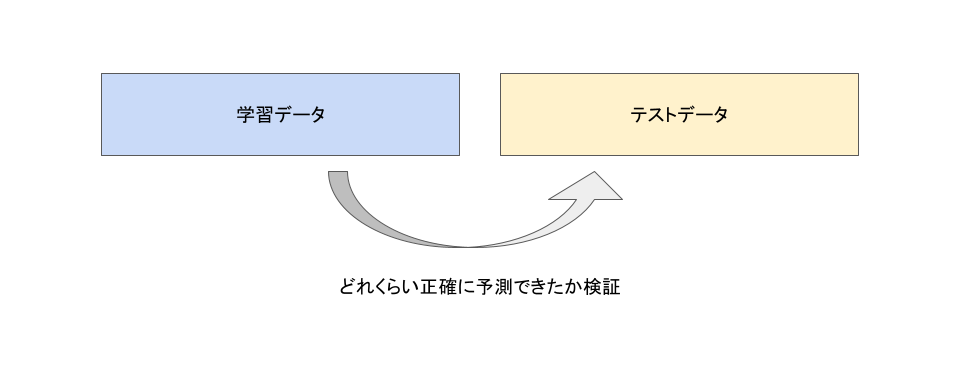
まずは学習データを使って予測モデルを作成し、テストデータを使って実際に予測値を算出します。
この予測値とテストデータの実際の値(正解値)のズレを比較すればモデルの性能を判定します。
クロスバリデーションを行う理由：過学習（オーバーフィッティング）を避ける
クロスバリデーションを行う理由は、モデルの性能(精度)を検証するためです。
モデルを作った時はモデルの性能を必ず確かめる必要があります。
なぜなら精度の低いモデルを作っても意味がないからです。
極端な話をいうと、予測するデータと全く関係のないデータを使っていたとしても、モデルを作ることは可能です。
しかし予測するデータと全く関係ないデータを使ってモデルを作った場合、そのデータに対して過剰に適合するようにモデルが作られます。
そのことを過学習（オーバーフィッティング）してしまう、という風に呼ぶことがあります。
たとえば明日の天気を予測するために靴を投げて表が出たかどうかのデータを使って予測モデルを作成することは出来ます。
ただ、もちろんそんなデータから作ったモデルで別のデータを当てはめたときの精度は低いですね。
というのも、「靴を投げて表が出たかどうかのデータ」に対して過剰にフィットしたモデルになっているため、別データに対しての予測精度が低くなるからです。
他にもデータ数が不十分であるなどの理由で、精度の低い予測モデルが出来ることがあります。
そのような意味のないモデルになっていないか検証するために、モデルを作ったら必ず精度を検証する必要があります。
このようにモデルを作る上で、クロスバリデーションはほとんどの場合で必要な作業です。
精度の評価にクロスバリデーションが優れる理由
クロスバリデーションをしなくても、解析をかけると決定係数やAICなどが算出されるためモデルの性能を評価することはできます。
しかし決定係数やAICなどの指標を使うよりも、クロスバリデーションの結果のほうが信頼できることが証明されています。
決定係数やAICなどの指標はあくまでも計算式で導き出した理論上の精度だからです。
実際に予測してテストしているクロスバリデーションの方が信頼性が高いことは当然なんです。
昔はコンピュータが発達しておらず、時間がかかるクロスバリデーションはできませんでした。
そのため決定係数やAICなどの指標がモデルの精度として使われてきました。
しかし最近は処理性能が高速になってきているため、クロスバリデーションが簡単にできるようになりました。
今後クロスバリデーションが必要になる機会はますます増えてくると思われます。
クロスバリデーションの手法
クロスバリデーションと言っても、実は様々な手法が提案されています。
では、クロスバリデーションには具体的にどのような手法があるのでしょうか？
ホールドアウト検証
最初に学習データとテストデータを8:2や7:3の比率で分割し、検証を行う方法です。
シンプルですので初心者に優しい手法です。
デメリットは2つあります。
1つ目は分割の仕方によって結果に差が出てしまうことです。
2つ目は、学習データのデータ数が減ってしまうため、データ総数が少ないと精度が落ちてしまうところです。
データ総数が少ない時は以下の方法を用いましょう。
1つ抜き交差検証(Leave one out cross validation：LOOCV)
1つ抜き交差検証は先ほどあげたホールドアウト法の欠点を改善したものです。
1つ抜き交差検証では、テストデータにするのは1つのデータのみです。
まずは1番目のデータをテストデータに、1番目以外のデータを全て学習データにして検証します。
次に2番目のデータをテストデータに、2番目以外のデータを全て学習データにして検証します。
このようにデータの数だけ何回も繰り返し検証を行い、全ての結果を平均したものを最終結果として算出します。
これなら学習データが減ってしまうこともありませんし、分割方法によって結果が変わることもありません。
一見便利な1つ抜き交差検証ですが、デメリットもあります。
何回も検証を繰り返すため、データ数が多いと計算に非常に時間がかかってしまう点です。
いくつかのモデルを交差検証したい時に、一つ一つに時間をかけるわけにはいかないので、たくさんのデータを扱う場合は1つ抜き交差検証はおすすめされません。
k分割クロスバリデーション（k-fold cross validation）
ホールドアウト検証や1つ抜き交差検証のいいとこ取りをしたのがk分割クロスバリデーションです。
kには5や10などの数字が入ります。
5分割クロスバリデーションの場合、まず全てのデータを5分割します。
そしてそのうち1つの分割データをテストデータとし、残りの4つの分割データを学習データとして交差検証を行います。
これを1つ抜き交差検証と同様に、テストデータを1番目の分割データ、2番目の分割データ、、、とデータを変えて5回繰り返し交差検証し、全結果の平均を最終結果とします。
1つ抜き交差検証よりも計算が短くて済み、学習データが少なくても使える点から、非常に便利な手法です。
デメリットは強いて挙げるなら、ホールドアウト検証に比べて手順が煩雑なところです。
クロスバリデーションの手順を分かりやすく解説！
クロスバリデーションが必要な理由と、その種類はわかった。
じゃあ実際にどうやるのか？という疑問にお応えしていきますね。
クロスバリデーションが登場する解析内容：モデルの良し悪しを判断できる
クロスバリデーションが活躍する代表例は、無数にあるモデルから最適なモデルの選択する時です。
機械学習モデルや多変量解析の手法は無数にあります。
たとえば「ある病気にかかっているかどうか診断をするモデル」を作るにしても、以下のモデルが候補に挙がります。
- ロジスティック回帰モデル
- サポートベクターマシン
- ランダムフォレスト
- 勾配ブースティング木
クロスバリデーションで検証しないことには、どのモデルの精度が一番良いのか分かりません。
上記のようなケースでは各モデルの精度をクロスバリデーションで検証し、最適なモデルを採用します。
クロスバリデーションを使った最終モデル選択までの流れ
最終モデルを選択、作成するまでの流れは以下のようになります。
- 使うモデルの候補をあげる
- それぞれのモデルでクロスバリデーションを行い、感度や特異度などの精度を算出する
- クロスバリデーションの結果、テストデータでの精度が一番高そうなモデルを選択
クロスバリデーションを活用する方法がイメージできたでしょうか？
今回は病気にかかっているか否かを判別するモデルでご説明しましたが、回帰モデルでもほとんど同じ流れです。
回帰モデルの場合は精度の指標に感度や特異度ではなく、RMSE(Root Mean Square Error)やAUC（ROC曲線下面積）を使います。
まとめ
最後におさらいをしましょう。
- クロスバリデーションとは機械学習モデルの性能を検証すること
- 決定係数などより正確に精度を検証でき、モデルの選択に不可欠
- ホールドアウト検証やk分割クロスバリデーションなどの手法がある
- 実際にモデル選択の際はクロスバリデーションで一番精度の高いモデルを採用する
記事中でも触れた通り、クロスバリデーションを使う機会は今後ますます増えてくると思われます。
是非使いこなせるようになって下さいね！
最後までお読み頂きありがとうございました。
動画でも解説していますので、ご参考まで！
第1章：臨床研究ではなぜ統計が必要なのか？計画することの重要性
第2章：研究目的をどれだけ明確にできるのかが重要
第3章：p値で結果が左右される時代は終わりました
第4章：多くの人が統計を苦手にする理由
第5章：統計を使えるようになるために今日から何をすれば良いか？
第6章：統計を学ぶために重要な環境
もしあなたがこれまでに、何とか統計をマスターしようと散々苦労し、何冊もの統計の本を読み、セミナーに参加してみたのに、それでも統計が苦手なら…
私からプレゼントする内容は、あなたがずっと待ちわびていたものです。
