適合度検定とは？カイ二乗検定を使う理由や独立性の検定との違い、Hosmer-Lemeshow検定（ホスマー・レメショウ検定）も解説！

適合度検定は、統計解析の時に使う仮説検定の一つです。

ただ仮説検定はいろいろな検定がありすぎるので、

• 「適合度検定ってどんな時に使う検定なの？」
• 「適合度検定と独立性の検定って何が違うの？」

といった疑問を持っている方も多いはずです。

本記事では適合度検定とは何か？ということや、カイ二乗検定を使う理由、独立性の検定との違いについて例を使って分かりやすく説明していきます。

適合度検定とは？

まずは、適合度検定が役立つ場面や使える条件を整理しましょう！

適合度検定が役立つ場面

適合度検定とは、あるデータの比率が理論上の比率と差がないか検証する統計手法です。

どんな時に使うのか、簡単な例を挙げますね。

被験者をランダムに集めた時に男女の比率が4:6だったとしましょう。

理論上の男女の比率は5:5であるはずなので、少しズレがあるように思いますね。

この実際の比率と理論上の比率の差が偶然なのかどうか確かめる時に使うのが適合度検定です。

もし偶然であればそのままその被験者で研究を進めても大丈夫です。

でも偶然じゃない差であれば被験者の集め方に問題があるので、再検討が必要だということになります。

適合度検定が使える条件

以下に適合度検定を使うときの条件をまとめました。

• データがカテゴリーデータ(比率で表せるならカテゴリーは何種類でも可能)
• データの理論比率が分かっている(本来ならこの比率になるはず！という値)

反対にデータが”年齢”のような比率で表せない連続値である場合や、理論比率が分からない場合には適合度検定を使うことはできません。

どうしても連続値に対して適合度検定したい場合は、例えば年齢なら10歳ごとに分けてカテゴリーデータにしてしまうという手もあります。

これなら10代はXX%,20代はYY%といった感じで比率にできますよね。

いかがでしょう？

適合度検定がどんな時に役立つのか、イメージしていただけたでしょうか？

ここからは適合度検定の中身について、詳しく解説していきますね。

適合度検定がカイ二乗検定なのはなぜ？

適合度検定はカイ二乗検定を使うことで理論比率と実測比率の差が偶然か、そうでないかを検証しています。

なぜカイ二乗検定なのか、疑問に思った方もいるのではないでしょうか？

まずはカイ二乗検定について解説した後、適合度検定の計算方法についてご説明していきますね。

適合度検定にはなぜカイ二乗検定が使われているのか？カイ二乗検定が有効な場面

カイ二乗検定はある群とある群の比率に差があるかどうか検証する統計手法です。

カイ二乗検定の計算の流れを簡単に説明すると、以下のようになります。

1. データをクロス集計表にまとめる
2. ある群とある群の差がない場合の理論値を算出
3. 理論値と実測値とのズレを計算
4. カイ二乗分布を使って理論値とのズレが偶然である確率(p値)を算出
5. p値が有意水準より小さければある群とある群に差があると判断

カイ二乗検定のポイントは理論値と実測値とのズレを検証している点です。

「あれ、適合度検定と一緒じゃん！」となった方は筋がいいですね。

次に適合度検定の計算方法をみていきましょう。

ちなみにカイ二乗検定について詳しく知りたい方は、こちらの記事で詳しく解説しています。

適合度検定の計算方法

今度は適合度検定の計算の流れを簡単に説明していきましょう。

1. データをクロス集計表(度数分布)にまとめる
2. 理論値と実測値とのズレを計算
3. カイ二乗分布を使って理論値とのズレが偶然である確率(p値)を算出
4. p値が有意水準より小さければある群とある群に差があると判断

いかがでしょうか？

適合度検定とカイ二乗検定は、実はほとんど同じ計算をしているのです。

カイ二乗検定の本質は理論値と実測値の差が偶然かどうか検証することですので、適合度検定にカイ二乗検定が使われるのは必然といえますね。

以上が適合度検定でカイ二乗検定が使われる理由です。

「目的が違うだけで、結局似たような計算をしているんだな〜」という感じでイメージしてもらえれば嬉しいです！

次は適合度検定と独立性の検定の違いについて説明していきますね！

適合度検定と独立性の検定の違い！ロジスティック回帰分析の予測で適合度検定が使われる理由は？

適合度検定と独立性の検定の違いは、その目的にあります。

• 適合度検定→あるデータが理論比率と異なるか検証したい
• 独立性の検定→ある群とある群の比率が異なるか検証したい

実は独立性の検定とは、ここまで”カイ二乗検定”として紹介してきた検定のことです。

ここまでご説明したように、適合度検定とカイ二乗検定(独立性の検定)の計算方法はほとんど同じです。

唯一違うのは、理論値の定め方だけです。

• 適合度検定の理論値→事前に決めた値
• 独立性の検定の理論値→2群の差がないと仮定した時の値

どちらの検定を使うか迷った時は、なぜその検定を行うのか、一度振り返って考えてみるといいですよ！

ロジスティック回帰分析の予測モデルで適合度検定が使われる理由は？

少しだけ脇道に逸れてしまいますが、ロジスティック回帰分析で適合度検定の結果が出てくることがあります。

JMPでロジスティック回帰分析を実施すると「モデル全体の検定」という名前で出力されます。

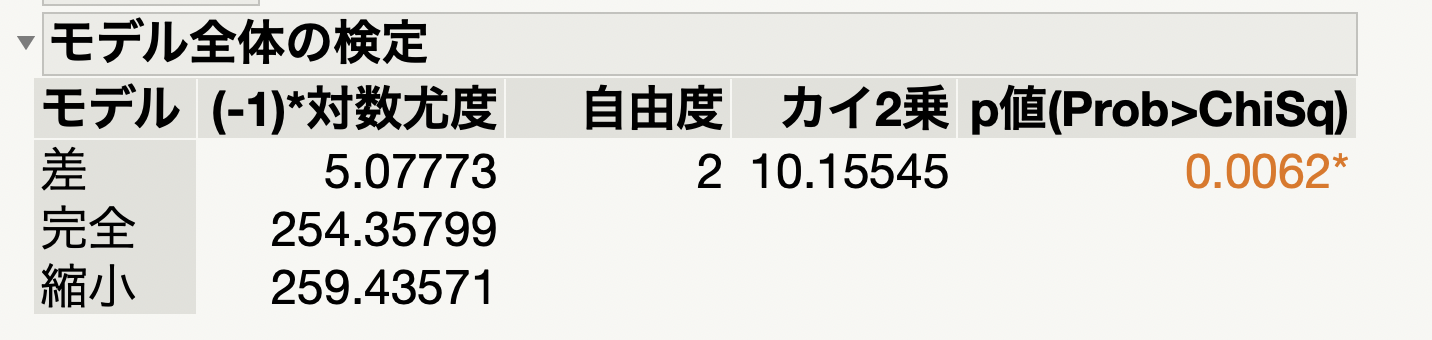
なぜロジスティック回帰分析で適合度検定が実施されるのでしょうか？

ここで一度、適合度検定が適用できる条件をおさらいしてみます。

適合度検定が適用できる条件はこれでした。

• データがカテゴリーデータ(比率で表せるならカテゴリーは何種類でも可能)
• データの理論比率が分かっている(本来ならこの比率になるはず！という値)

ロジスティック回帰はそもそも2値のカテゴリカルデータを扱う回帰分析ですので、1つ目の条件は満たしています。

じゃあ2つ目の条件は？ロジスティック回帰での理論比率って何？って疑問がありますよね。

これは単純で、理論比率＝切片しかないモデル（説明変数がひとつもないモデル）として検定を実施しています。

つまり、「すべての説明変数に対するパラメータがゼロである（真のモデルは切片だけのモデルである）」という帰無仮説に対するカイ2乗の適合度検定です。

なので検定結果として有意差が出たとすると、「切片だけのモデルは不適切で、何かしら説明変数が必要だ」ということに、つまりは「現在のモデルは切片だけのモデルよりもいい」ということになりますね。

Hosmer-Lemeshow検定（ホスマー・レメショウ検定）との違いは？

ロジスティック回帰分析においてモデルの適合度を評価する際に用いられる検定は、上記のカイ二乗検定の枠組みを用いた適合度検定の他に、Hosmer-Lemeshow検定（ホスマー・レメショウ検定）があります。

Hosmer-Lemeshow検定（ホスマー・レメショウ検定）の帰無仮説は「モデルがデータに適合している」ということであるため、p値が有意水準（通常は両側0.05）を上回っていれば、適合度が良いと判断されます。

ただし、サンプルサイズが小さい場合には検出力が小さい（つまり、有意になりにくい）ため、本当に適合しているかどうかの判断は慎重にする必要があります。

内田（2004）の報告によると、シミュレーションによって以下の現象が観測されています。

• 適合度不良モデルを乱数データとして発生させた場合
  • サンプルサイズ50で、p値が0.476（適合していると誤って判断）
  • サンプルサイズ100で初めてp=0.036と、適切な判断をした
• 適合度良好モデルを乱数データとして発生させた場合
  • 決定係数（R二乗値）が0.756のモデルでp=0.812
  • 同じモデルでのカイ二乗検定ではP<0.001

つまり、Hosmer-Lemeshow検定（ホスマー・レメショウ検定）は小規模データでは適合度不良を検出できないリスクを持っていることを示唆しています。

＞＞EZRでロジスティック回帰のHosmer-Lemeshow検定（ホスマー・レメショウ検定）を実施する方法

適合度検定の例をわかりやすく解説！

ここからは実際に適合度検定を行うまでの流れを簡単な例を使って解説していきますね！

使うツールはEXCELだけですのでご安心くださいね！

適合度検定のための事前準備

例として、ある研究をするために同じ病院内でランダムに集めたデータの疾患比率に偏りがないか検証したいとしましょう。

事前準備として考えておかないといけないのは、以下の3点です。

• 何の比率を検証するのか？
• 理論比率はどれくらいか？
• 有意水準はどれくらいにするか？

何の比率を検証するのか？

今回検証するのは疾患比率です。

「整形」「脳血管障害」「心疾患」「その他」の4つのカテゴリーに分けて疾患比率を検証していくことにしました。

理論比率はどれくらいか？

適合度検定をする場合、理論比率を定めなければなりませんでしたね。

今回は病院内の被験者を正しくランダムに集められたかどうかを確かめたかったので、病院全体の疾患比率を理論比率としました。

調べた結果その病院の患者は「整形：脳血管障害：心疾患：その他=4:3:2:1」の疾患比率でしたので、この値を理論比率とします。

ちなみに他の病院と比べて比率に差があるか確かめたい時は、他の病院の疾患比率の情報が必要になります。

有意水準はどれくらいにするか？

最後に有意水準を決めなくてはなりません。

慣例にならってここでは有意水準を5%に定めました。

データをクロス集計表にまとめる

次はデータをクロス集計表にまとめます。

今回のデータはこのようなクロス集計表になりました。

理論比率を追加すると以下のようになります。

このクロス集計表を使ってカイ二乗検定を実行します。

カイ二乗検定を実行する

カイ二乗検定を実行してp値の算出するためにはEXCELの”CHISQ.TEST関数”を使用します。

以下のように好きなマスに“=CHISQ.TEST(実測値,期待値)”と入力しましょう。

後はEnterを押せばp値を自動で算出してくれます。

今回はp=0.02で有意水準5%を下回ったため、疾患比率に偏りがあるという判断ができます。

どうやらデータがランダムに集められておらず、集め方に問題があったのかもしれませんね。

まとめ

最後におさらいをしましょう。

データの分布に偏りがないか確認することは、研究では非常に重要です。

そのため適合度検定を使うことでデータの比率を確認することは、より質の高い研究に繋がります。

EXCELだけでも簡単にできる検定ですので、ぜひ活用してみてくださいね！

最後までお読みいただきありがとうございました。

統計に関するご質問があれば、メルマガにご登録の上ご質問くださいませ！

＞＞メルマガ登録はこちら（無料プレゼントあります。）