この記事では「EZRで主成分分析をする方法!Rコマンダーの機能を使ってわかりやすく解説!」ということでお伝えしていきます。
主成分分析ってなんとなく難しい解析のように思えますが、ちゃんと手順を整理すればそれほど難しい解析ではありません。
無料で使えるEZRで、ぜひ主成分分析をできるようになりましょう!
EZRで解析する前に主成分分析をちょっとだけ解説!

主成分分析は「多くの変数の情報をできるだけ損なわずに、少数の変数に縮小させることを目的とした解析手法」です。
例えば、体重と身長という2つの変数がある場合に、BMIという1つの変数に縮小させる、と言うようなイメージを持っていただければOK。
ただし主成分分析の注意点としては、主成分分析自体は「少数の変数に縮小させる」という目的だけであり、縮小させた変数をどう使うかはまた別問題である、ということ。
そのため、主成分分析をした後に何を知りたいのか?という目的が明確ではないと、主成分分析をした後の結果の解釈ができなくなります。
この記事では、EZRで主成分分析を実施する方法までを解説して、主成分分析をした後にどんなことをすべきか?というのは対象外になります!
EZRで主成分分析を実施する!Rコマンダー機能を使えばできます

主成分分析はEZRでも実施可能です。
実際に「主成分分析(PCA)とは?手順や用語の解説を含めてわかりやすく解説!」の記事で解説した3つの手順に従ってやってみましょう!
3つの手順は以下の通りです。
- なぜ主成分分析をするのか、目的を明確にする
- データを解析できる状況にする
- 統計ソフトで解析する
EZRで主成分分析の手順1:なぜ主成分分析をするのか、目的を明確にする
この部分はEZRで解析する前に是非ともご自身で考えていただきたい部分です!
前述の通り、主成分分析をしただけでは変数を縮小することにしかなりません。
主成分分析した後の変数をどう解釈し、そしてどう使うか。
そのようなことをハッキリさせておかないと、主成分分析をやりました、だけで終わってしまいますので。
EZRで主成分分析の手順2:データを解析できる状況にする
ここから実際のEZRでの手順に入っていきますね。
データは架空のデータを使ってみます。
47人分(47行)に対して、変数がA〜I(9つの変数)がある状況を想定します。
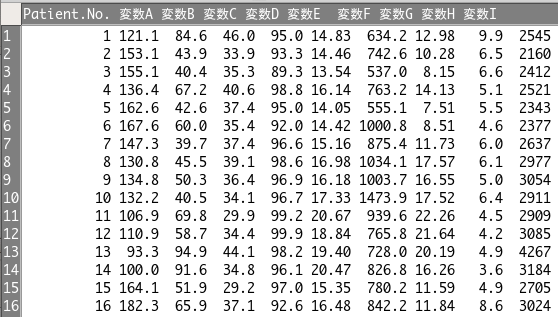
この時、データを見ると変数ごとに桁数などが全然違うため、おそらく単位が全く異なる変数なんだな、と見当がつきます。
なので、標準化をする必要がありますね。
標準化とは、平均0,SD1にするデータ変換のことでした。
標準化はEZRで簡単に実施することができます。
「標準メニュー」→「データ」→「アクティブデータセット内の変数の管理」→「変数の標準化」を選択します。
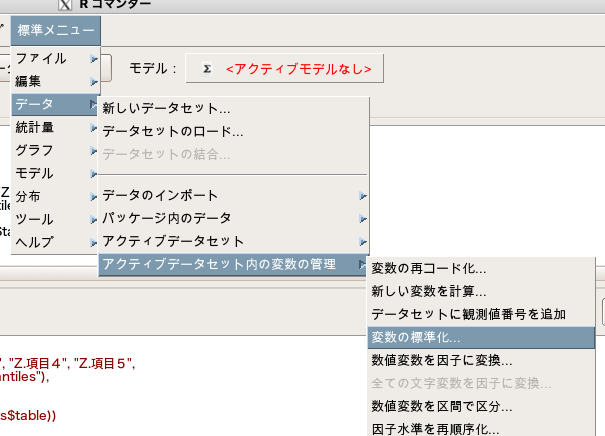
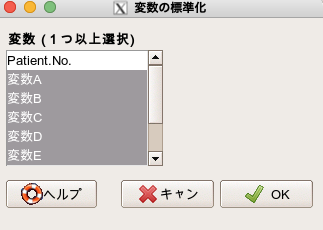
すると以下のコマンドが出てきますので、標準化したいデータを全て選択します。
そしてOKを押す。
この操作により、元のデータセットに標準化された変数が自動的に格納されます。
(変数名が「Z.元の変数名」であるものが、標準化された変数です)
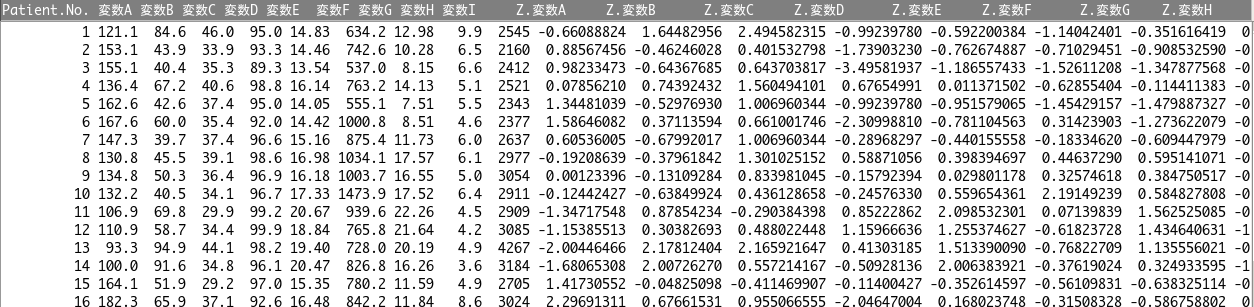
じゃあ本当に標準化できたの?と思いますので、標準化されたデータの要約統計量を算出してみます。
すると以下のようになりました。

平均値にある「e-16」は「10のマイナス16乗」の意味なので、「めちゃめちゃ小さい」ということがわかります。
つまり、限りなく0である、ということですね。
そして標準偏差は全ての変数で1です。
無事に標準化ができたということになります。
EZRで主成分分析の手順3:統計ソフトで解析する
データの標準化までできたので、ここからEZRで主成分分析を実施していきます。
EZRでは標準メニュー(Rコマンダーのメニュー)で主成分分析を実施することができ、「標準メニュー」→「統計量」→「次元解析」→「主成分分析」を選択します。
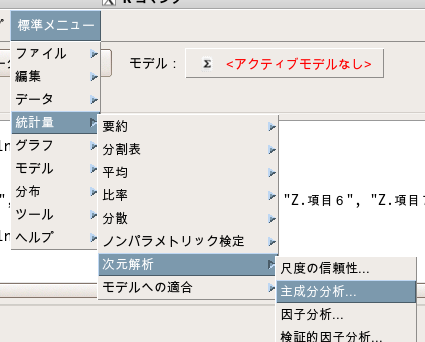
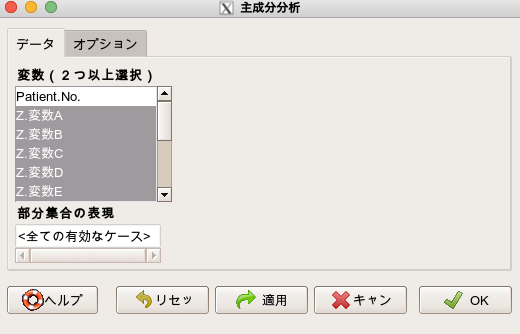
すると以下のパネルが出てきますので、主成分分析を実施したい変数を選択します。
今回は、Z.変数A〜Z.変数Iまでの9つの変数を選択します。
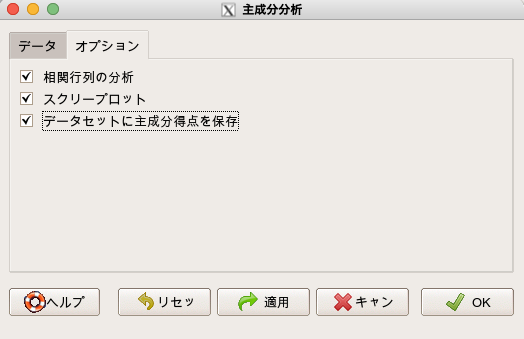
そして「オプション」のタブをクリックし、3つのチェックボックスに全てチェックを入れておきます。
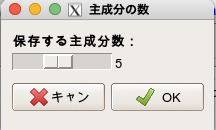
OKを押すと、データセットに保存する主成分得点はどの主成分までにするかを聞かれますので、ここでは5にしておきます。
そしてOKを押せば、無事に主成分分析ができました。
EZRで主成分分析を実施した結果を解釈する!

ではEZRで主成分分析ができましたので、結果を見ていきましょう。
まず結果として出てくるのが、「Component loadings」という結果。
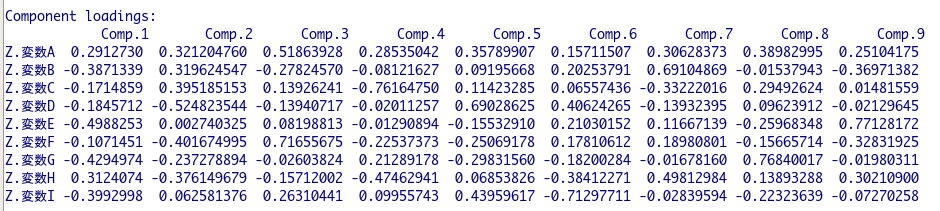
上記の結果がいわゆる「固有ベクトル」と呼ばれるものです。
固有ベクトルとは、各変数に対する回帰係数を示しています。
そのため第一主成分は、以下の回帰式で表すことができるということ。
0.29*Z.変数A – 0.39*Z.変数B – 0.17*Z.変数C – 0.18*Z.変数D – 0.50*Z.変数E – 0.11*Z.変数F – 0.43*Z.変数G + 0.31*Z.変数H – 0.40*Z.変数I
次に表示されているのは「Component Variance」です。
この結果がいわゆる「固有値」の結果です。
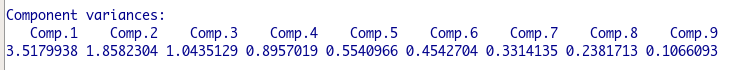
そして最後に「Importance of components」の出力。
Standard deviationは分散をルートしたもの。
Proportion of Varianceがいわゆる「寄与率」であり、Cumulative Proportionが「累積寄与率」です。

今回の結果を見ると、第一主成分は元の変数の約39%の情報を持っており、第4主成分までで元の変数の約81%の情報を持っていることになります。
じゃあどこまでの主成分を採用するか?と言えば、一般的には70%か80%程度の累積寄与率があれば良いとも言われていますので、第三主成分か第四主成分までで結果の解釈やその後の解析を進める、と言った流れになります。
まとめ

いかがでしたか?
この記事では「EZRで主成分分析をする方法!Rコマンダーの機能を使ってわかりやすく解説!」ということでお伝えしました。
主成分分析ってなんとなく難しい解析のように思えますが無料で使えるEZRで、割と簡単に実施することができましたね。
ぜひEZRで主成分分析をマスターしましょう!













コメント