今回の記事では「コクランアーミテージ検定をEZRで実施!傾向検定はどんなパターンで有意差ありになる?」としてお伝えします。
- コクランアーミテージ検定ってそもそもどんな検定?
- コクランアーミテージ検定をEZRで実施する方法
- 色んなデータのパターンにコクランアーミテージ検定を実施するとどうなるか
ということが理解できるようになりますよ!!
コクランアーミテージの傾向検定とは?

コクランアーミテージの傾向検定は、順序変数の水準間における二項割合の傾向を調べる検定です。
例えば、「低用量・中用量・高用量で、反応割合の傾向があるか?」という疑問がある場合に適用できる検定。
コクランアーミテージ検定が適用できる条件としては2つ。
- 応答変数(目的変数)は、2値のカテゴリカル変数
- 説明変数は、順序カテゴリカル変数
この2つを満たす場合に適用可能です。
コクランアーミテージ検定の帰無仮説と対立仮説は?
コクランアーミテージ検定も統計的検定の一つなので、帰無仮説と対立仮説があるはず。
さまざまな書籍やサイトを見ると、帰無仮説は「割合の傾向がない」とか「説明変数の全水準において二項割合が同じ」という記載もみますが、私としては以下の帰無仮説と対立仮説がわかりやすくイメージしやすいかなと思います。
- 帰無仮説:直線の傾きが0である
- 対立仮説:直線の傾きが0ではない
割合の点推定値に対して、説明変数の水準の順番に線を引くと傾きが0ではない場合、検定結果は有意になるはず、ということですね。
例えば以下の場合、用量が大きくなるにつれて反応する割合が多くなる(薄いグレーの部分が大きくなる)ため、傾きが0ではない直線が引けそうです。
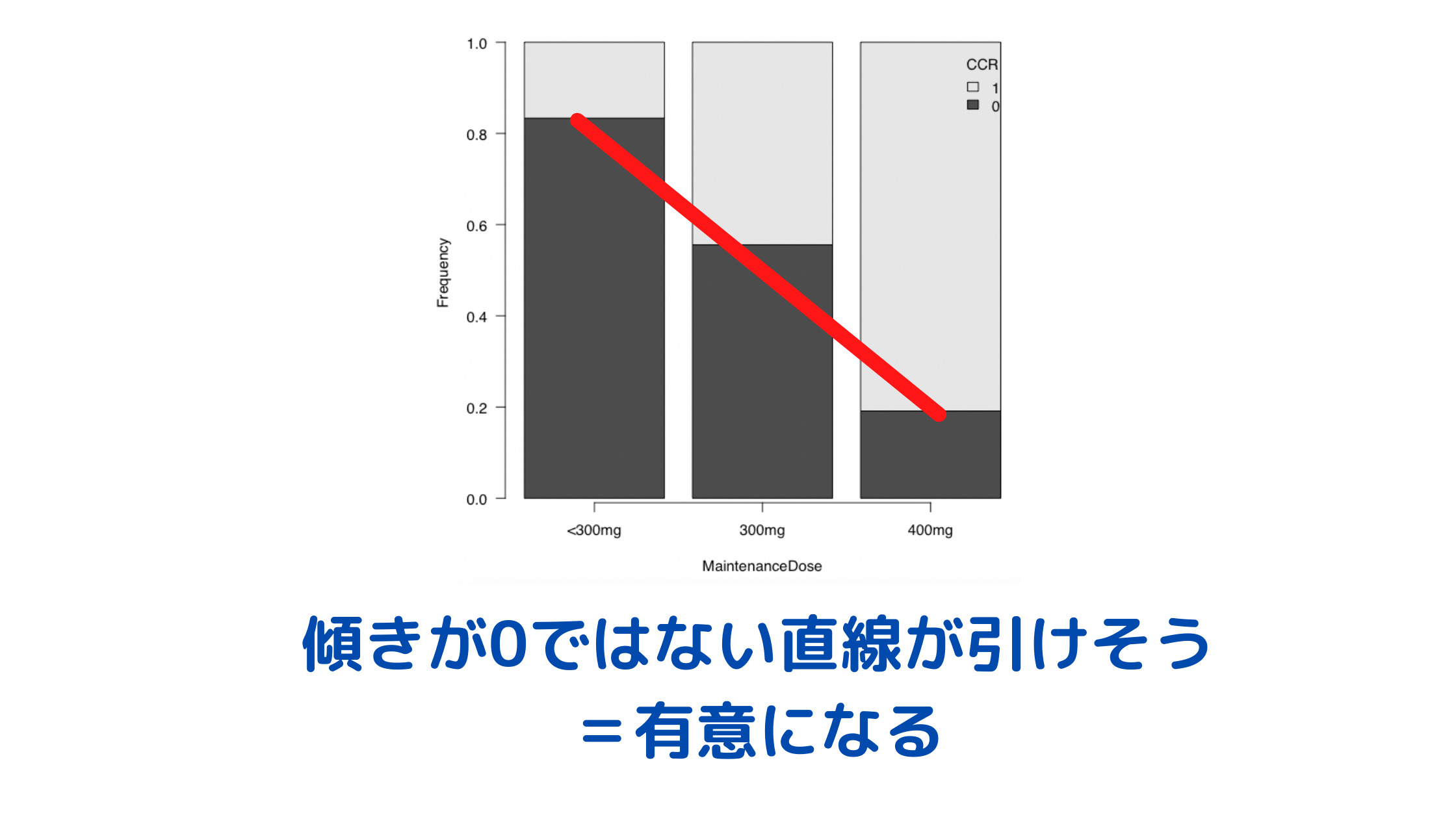
一方で以下の場合、用量が大きくなるにつれて反応する割合が多くなる(薄いグレーの部分が大きくなる)わけではないため、傾きが0ではない直線が引けなさそうです。
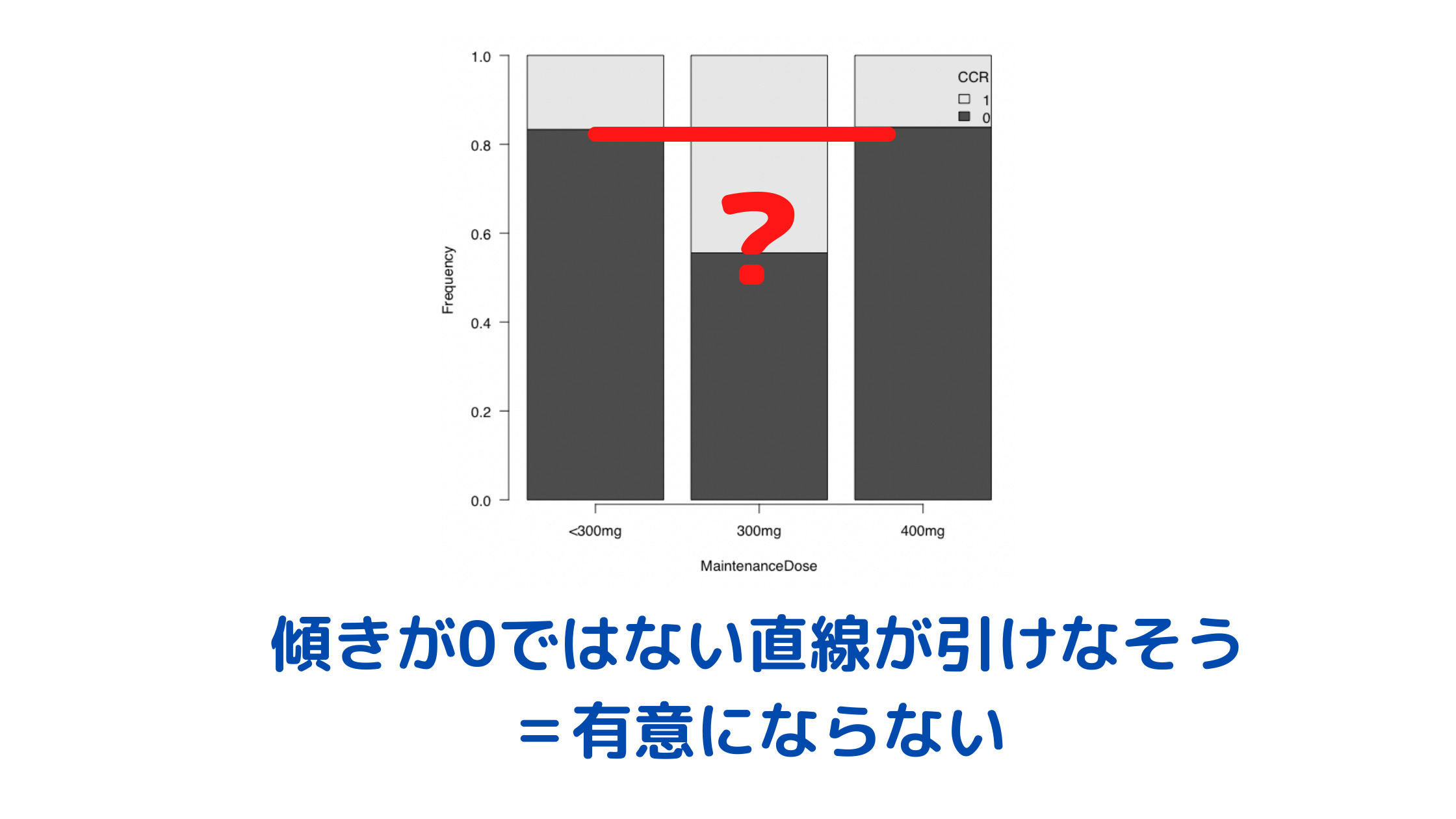
コクランアーミテージ検定をEZRで実施してみる

ではここから、コクランアーミテージ検定をEZRで実践してみましょう。
データは「EZRでやさしく学ぶ統計学」に付いているデモデータを用います。
データの作り方での注意点としては、「EZRでは順序変数はアルファベット順に認識される」という点。
説明変数である順序カテゴリカル変数が、解析したい順番になっていない場合は、事前に「因子水準を再順序化する」で順番を整理しておく必要があります。
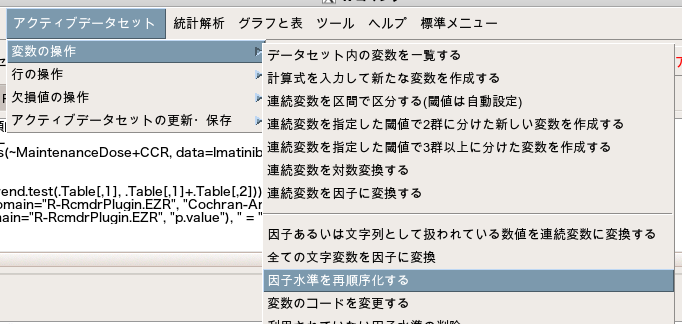
状況としては、あるがん腫において
- 薬剤投与が<300mg, 300mg, 400mgという3つの用量データ
- 反応が「有効」かどうかの2値のカテゴリカルデータ
というデータになっていて、解析の目的は「薬剤の投与量が多ければ有効割合が多くなる傾向があるか?」ということです。
割合のグラフを描いてみるとこんな感じ。
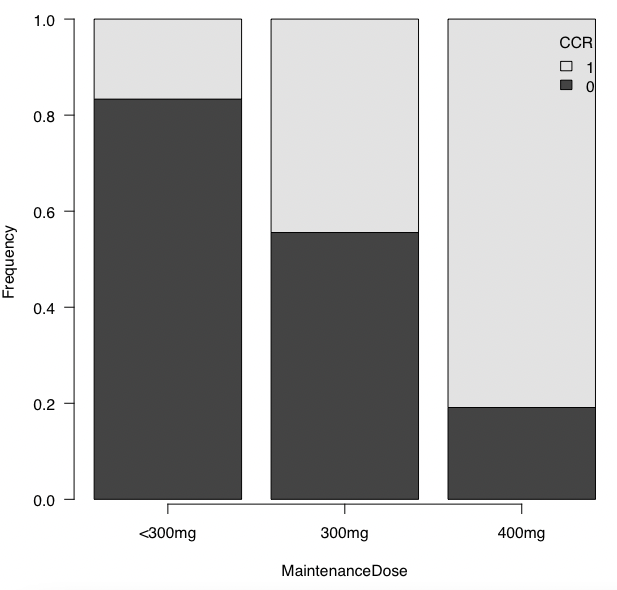
傾向がありそうですね。
それを検定を用いて判断してみます。
EZRでコクランアーミテージ検定を実践!
EZRでコクランアーミテージ検定を実施するには、「統計解析」>「名義変数の解析」>「比率の傾向の検定」を選択します。
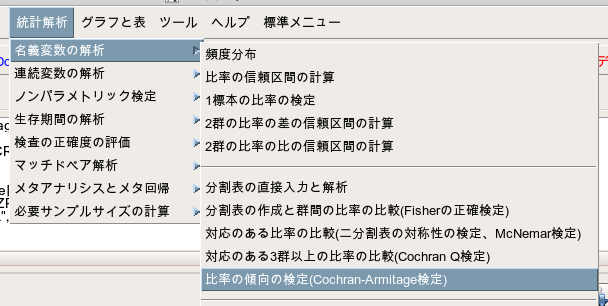
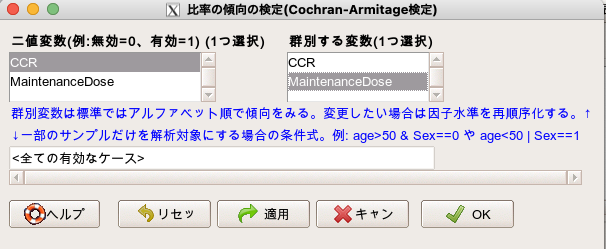
すると下記のような画面になりますので、
- 左側の二値変数には、目的変数となる2値のカテゴリカル変数を選択
- 右側の群別する変数には、説明変数となる順序カテゴリカル変数を選択
これでOKを押します。
すると、下記のような結果が得られました。

P値は有意水準である0.05を下回っていますので、有意差あり。
つまり、直線の傾きが0ではない(傾向がある)という結論になります。
色んなパターンにコクランアーミテージ検定を適用するとどうなる?

先程の例は、傾向がありそうなデータでコクランアーミテージ検定を実施しました。
しかし実データでは、必ずしも傾向がありそうなデータだけじゃないですよね。
そのため、以下の2パターンでコクランアーミテージ検定を実施するとどうなるかをやってみましょう。
- 「低用量の割合=中用量の割合<高用量の割合」の場合
- 「低用量の割合=高用量の割合<中用量の割合」の場合
パターン1:「低用量の割合=中用量の割合<高用量の割合」でのコクランアーミテージ検定
まずは「低用量の割合=中用量の割合<高用量の割合」の場合です。
状況としては、下記の通り。
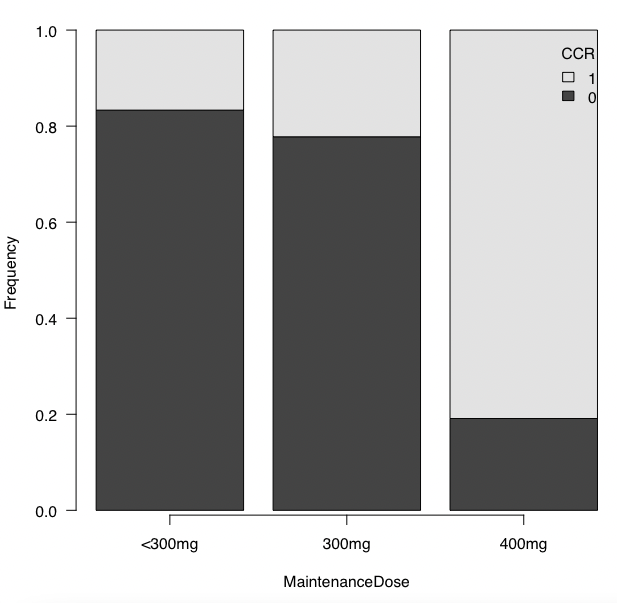
「<300mg」群と「300mg」群で反応の割合がほぼ同じであり、「400mg」群だけ反応が大きくなっているパターンです。
この場合にEZRでコクランアーミテージ検定を実施してみると、以下の結果に。

P値は有意水準である0.05を下回っていますので、有意差あり。
つまり、直線の傾きが0ではない(傾向がある)という結論になります。
パターン2:「低用量の割合=高用量の割合<中用量の割合」でのコクランアーミテージ検定
次は、「低用量の割合=高用量の割合<中用量の割合」の場合です。
パターンとしては以下の通り。
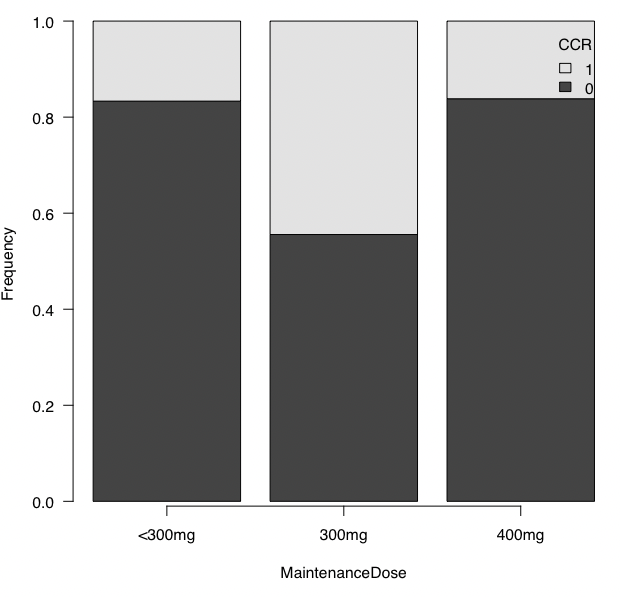
「<300mg」群と「400mg」群で反応の割合がほぼ同じですが、真ん中の「300mg」群だけ反応が大きくなっているパターンです。
この場合にEZRでコクランアーミテージ検定を実施してみると、以下の結果に。

つまり、直線の傾きが0ではないとは言えない(傾向があるとは言えない)という結論になります。
まとめ

いかがでしたか?
今回の記事では「コクランアーミテージ検定をEZRで実施!傾向検定はどんなパターンで有意差ありになる?」としてお伝えしました。
- コクランアーミテージ検定ってそもそもどんな検定?
- コクランアーミテージ検定をEZRで実施する方法
- 色んなデータのパターンにコクランアーミテージ検定を実施するとどうなるか
ということが理解できるようになったのなら幸いです!
こちらの内容は動画でもお伝えしていますので、あわせてご確認くださいませ。













コメント