要約統計量とは何を出力すればいい？研究データの要約に必要なもの

データが得られたら、何をする必要があるでしょうか？

• 一つ一つのデータを確認する？
• 平均値を出してみる？
• 統計的検定をしてみる？

実は、どれも正解です。

得られたデータが少なければ、一つ一つ確認することも可能ですし、むしろそれがとても重要な場面があります。

しかし、サンプルサイズが大きくなってデータ量も膨大になってしまうと、データを一つ一つ確認することは不可能に近いです。

その際には、データを要約してみる。

つまり、要約統計量を算出してみるということが重要です。

 

統計の役割は、２つありました。

それが、要約することと、計画すること。

このページでは、その中の１つである「データを要約する」ことに関して重要な要約統計量を解説します。

 

要約統計量とは？何を出力すればいいの？

では、いざ要約統計量を出力しよう！と言われても、何を出力すれば良いか、途方に暮れてしまいますよね。

2群間の比較の統計解析は？でも書きましたが、基本的には以下の表が作れればOKです。

（例えば、男性と女性ごとに要約統計量を出力したい場合です）

 

	男性	女性
平均値（SD）	XXX（XX）	YYY（YY）
中央値	XXX	YYY
範囲	XXX-XXX	YYY-YYY
四分位範囲	XXX-XXX	YYY-YYY
95%信頼区間	XXX-XXX	YYY-YYY

 

まとめると、以下の6つの指標が連続量（量的データ）の要約統計量には必要ですね。

1. 平均値
2. 標準偏差
3. 中央値
4. 四分位範囲
5. 範囲
6. 95%信頼区間

 

要約統計量として、これら6つの指標が出力されていれば、全く問題ないでしょう。

 

要約統計量のためのグラフ：ヒストグラムと箱ひげ図

要約統計量では6つの指標を出力すればOKということを学びました。

しかし、表に数値だけ出されても、あんまりイメージできないですよね。

そのため、ちゃんとグラフを使って可視化することも重要です。

 

要約統計量のためグラフは、2つあると便利です。

1. ヒストグラム
2. 箱ひげ図

 

ヒストグラムは、データが正規分布かどうかを把握するために重要なグラフになります。

箱ひげ図は、平均値、中央値、四分位範囲、範囲が一目でわかる、めちゃめちゃ便利なグラフです。

 

なので、先ほどの6つの要約統計量にプラスして、ヒストグラムと箱ひげ図を出力すれば、かなり良いデータの要約をしていることになります。

 

要約統計量の英語表現

英語論文を書く上で、各要約統計量の英語表現が必要ですよね。

そのため、上記の要約統計量の指標の英語表現をお伝えします。

ちなみに要約統計量自体の英語表現は、Summary Statisticsが用いられることが多い印象です。

 

1. 平均値：Mean
2. 標準偏差：Standard Deviation (SD)
3. 中央値：Median
4. 四分位範囲：Interquartile Range (IQR)
5. 範囲：Range
6. 95%信頼区間：95% Confidence Interval (95%CI)
7. ヒストグラム：Histogram
8. 箱ひげ図：Box plot

 

要約統計量として平均値と中央値以外の代表値

代表値とは、平均値や中央値などのように、データの特徴を表す統計量です。

要約統計量としては、平均値や中央値を出力する必要がありましたね。

そのほかにも、代表値としては最頻値があります。

最頻値とは、もっともデータが集中している値のことをいいます。

ヒストグラムを書いた時に、一番山が高い部分ですね。

たとえば、以下のヒストグラムであれば、170センチの階級の度数が一番多いので、ここが最頻値になります。

 

 

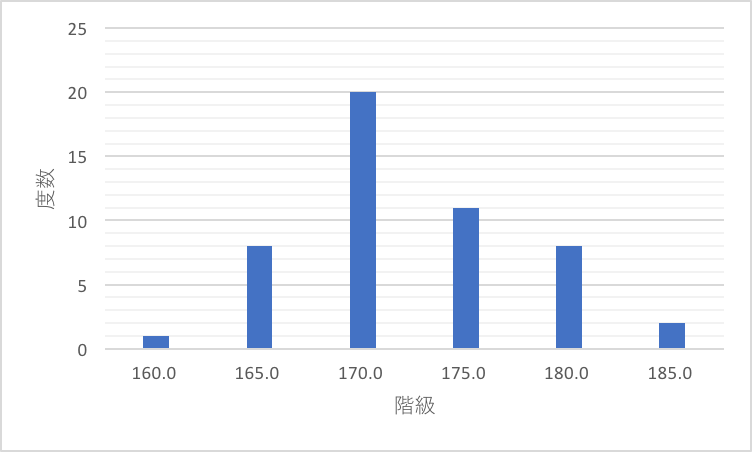
要約統計量として標準偏差や四分位範囲などのバラツキの指標の役割

データはばらつきます。

例えば、大学生の体重が知りたいという疑問があったとき、日本全国の大学生（母集団）の体重を知ることは実質不可能なため、近くの大学で10人（標本）の体重を教えてもらいました。

すると、以下のような表のとおりのデータが得られました。

	大学生１	大学生２	大学生３	大学生４	大学生５	大学生６	大学生７	大学生８	大学生９
体重	50.4	54.6	55.2	58.4	64.3	65.5	69.1	71.4	74.5

この表からまず分かるのは、「同じデータがない」ということです。

これは当たり前かと思いますが、同じデータがないと認識することからバラツキの指標を出力するということを考え出すからです。

同じデータがないため、私たちは平均値や中央値という代表値でデータの特徴をつかみ、さらにバラツキの指標を用いることでデータのイメージを膨らますことが出来ます。

その前提に立つと、どれぐらいばらついているのか？ということに興味が出てくるでしょう。

 

この時に重要なバラツキの指標が、標準偏差と四分位範囲です。

標準偏差は、平均値に対応したバラツキの指標。

一方の四分位範囲は、中央値に対応したバラツキの指標です。

 

要約統計量でデータを把握することは、とても重要

要約統計量で出力する指標、そしてヒストグラムと箱ひげ図。

これらを出力することは、それほど難しくありません。

でも、とても重要な統計解析の方法ですし、立派に統計解析をやっていると胸を張って言っていいです。

統計って難しいというイメージがあるので、なんとなくデータを要約しただけでは不十分なんじゃないの・・・？という不安を持つ方がいらっしゃるみたいですね。

でも、よく理解してもいない統計学的検定をやってみてP値が0.05を下回るかどうかで一喜一憂するよりも、要約統計量を出力してちゃんとデータと向き合うほうが、とても重要なのです。

 

「統計＝検定」ではない。

このことを再度認識してくださいね！

 

要約統計量に関するまとめ

要約統計量は、以下の6つの指標が必要です。

1. 平均値
2. 標準偏差
3. 中央値
4. 四分位範囲
5. 範囲
6. 95%信頼区間

このほかにも、要約統計量のためグラフは、2つ出力すると良い。

1. ヒストグラム
2. 箱ひげ図