この記事では「条件付きロジスティック回帰分析とは?傾向スコアマッチング後にも使う解析」ということでお伝えします。
弊社でサポートさせていただいた方がパブリッシュした論文レビュー(傾向スコアマッチングを使った論文)で、「マッチさせたという情報を考慮して解析する必要はないか?」というレビューコメントが来たことがあります。
そのコメントに対して今回の記事の通りの対応をしました。
そのため、もしあなたが傾向スコアマッチングを使った論文を考えているのであれば、今回の記事が役立つはずです!
条件付きロジスティック回帰:対応のあるデータやマッチングを考慮する解析
条件付きロジスティック回帰は、結論から言えば「対応のあるデータ(ケースコントロール研究など)やマッチングデータについて二項ロジスティック回帰分析を行う場合」に用いられる方法です。
なぜ通常のロジスティック回帰分析じゃダメなのか?と思いますよね。
通常のロジスティック回帰だと、「マッチングした」とか「対応がある」という情報が考慮されずに解析されてしまうことで、検出力が低くなる(有意になりにくくなる)というデメリットがあるからです。
以上の理由から、対応のあるデータ(ケースコントロール研究など)やマッチングデータについては、条件付きロジスティック回帰分析を実施するのが良いとされています。
ただ、「条件付きロジスティック回帰分析を必ずすべきかどうか」には議論があります。
つまり、検出力が小さいだけ(有意になりにくいだけ)であれば、通常のロジスティック回帰でもいいのでは?という意見もある、ということです。
私個人としても、通常のロジスティック回帰でもいいのでは?と思っております。
通常のロジスティック回帰と条件付きロジスティック回帰の違い
では、通常のロジスティック回帰と条件付きロジスティック回帰の違いは何なのでしょうか?
まず通常のロジスティック回帰を見てみます。
通常のロジスティック回帰では、下記のように共通の切片と共通の回帰係数を考えて解析しています。
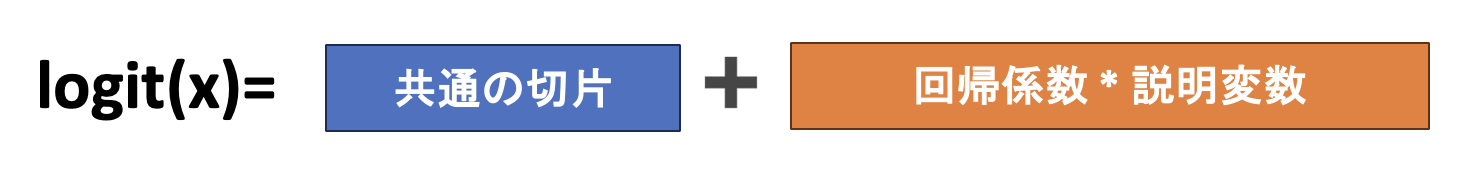
一方で条件付きロジスティック回帰は、考慮したい情報(マッチングの情報など)の各層(水準)ごとに、切片を考えるということをしています。
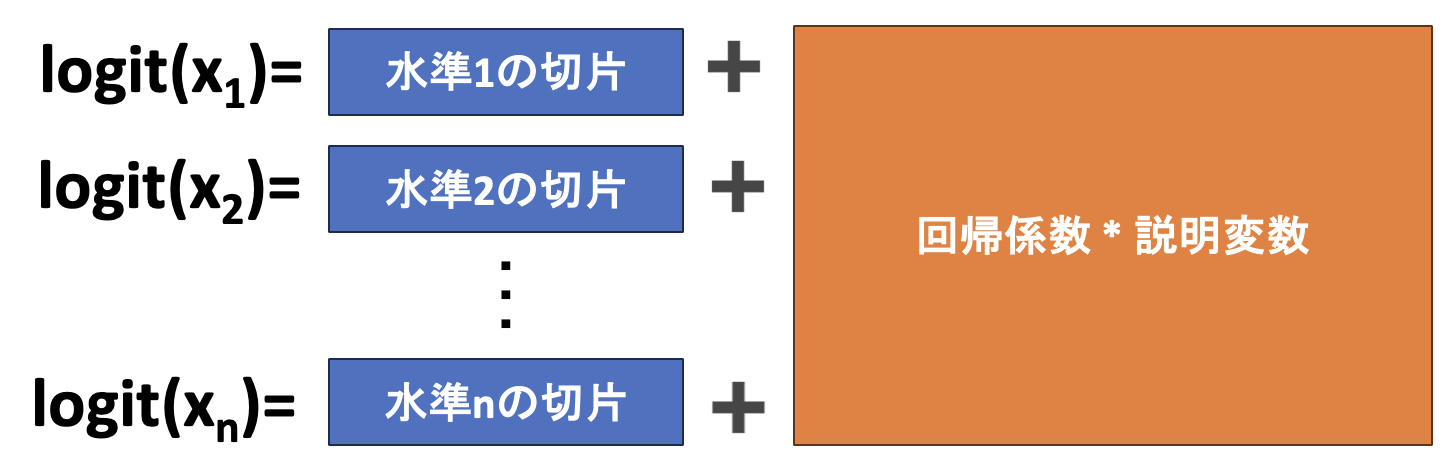
水準が変わっても、回帰係数は共通で考えているため、解析結果としてもオッズ比は各説明変数に一つだけ出力されるようになります。
(つまり、結果の解釈は通常のロジスティック回帰と同様に可能)
傾向スコア解析の後は条件付きロジスティック回帰が良いとされる

あまり馴染みのない条件付きロジスティック回帰ですが、医薬研究では傾向スコア解析(特に傾向スコアマッチング)の時に出てきます。
傾向スコア解析は条件付きロジスティック回帰分析を実施する状況を満たしているからです。
なぜかと言えば、「傾向スコア」という情報が似ている症例をまとめることができるため、傾向スコアを考慮して解析すべき、という考えがあるため。
ちなみに、傾向スコアマッチングの後にCox比例ハザードモデルを実施したい場合には、層別Cox比例ハザードモデルを実施することが良いとされています。
EZRで条件付きロジスティック回帰を実施する方法
では実際に、EZRで条件付きロジスティック回帰分析を実施してみます。
状況としては、傾向スコアを算出した、という前提で、その後に条件付きロジスティック回帰を実施してみる、という状況です。
傾向スコアを算出した後に条件付きロジスティック回帰分析を実施する方法は2つあります。
- 傾向スコアを元にして3〜5つの層を作成し、3〜5の層情報で条件付きロジスティック回帰分析を実施する
- 傾向スコアマッチングを実施し、マッチング情報を元にして条件付きロジスティック回帰分析を実施する
EZRで傾向スコアマッチングの実施方法はこちらの記事を参照してください。
>>EZRで傾向スコアマッチング!論文でもよく使われる方法をわかりやすく解説
傾向スコアを元にして3〜5つの層を作成し、3〜5の層情報で条件付きロジスティック回帰分析を実施する
まずは、傾向スコアを元にして3〜5つの層を作成し、3〜5の層情報で条件付きロジスティック回帰分析を実施す流方法についてお伝えします。
まずは、群を目的変数、交絡因子となる情報を説明変数とするロジスティック回帰分析を実施し、傾向スコアを計算します。
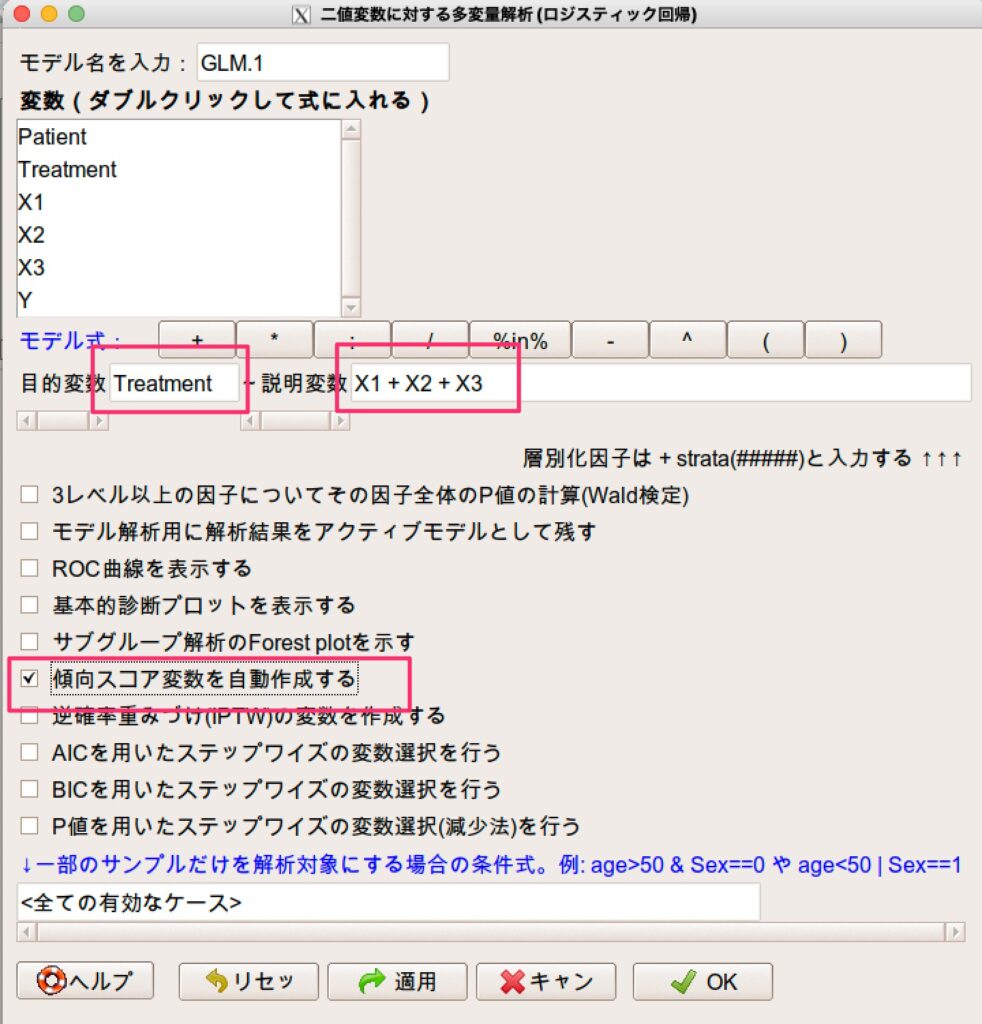
すると、データの中に傾向スコアが格納されます。
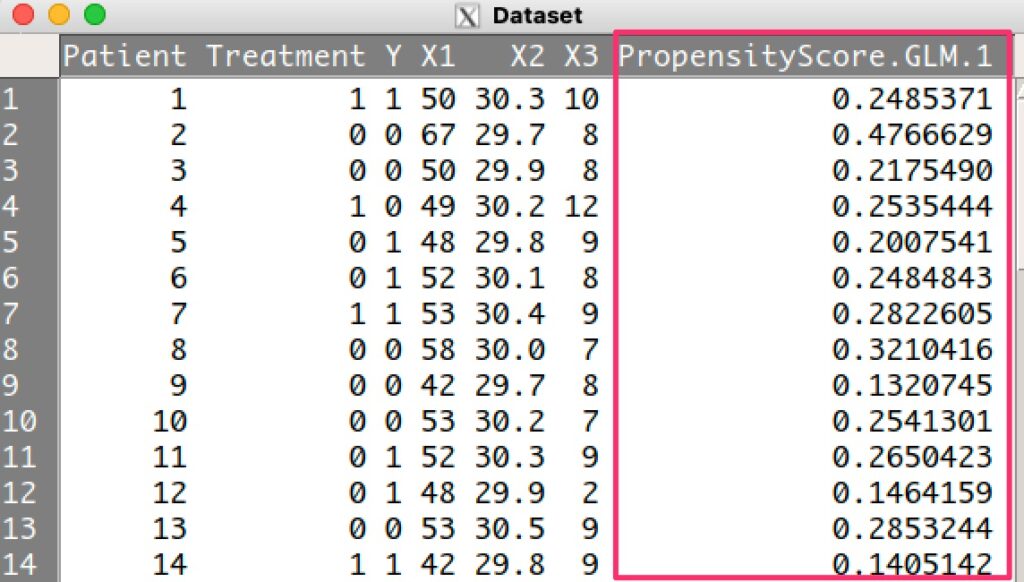
このとき、傾向スコアが連続量なので、3〜5つの水準のカテゴリカル変数に変換する必要があります。
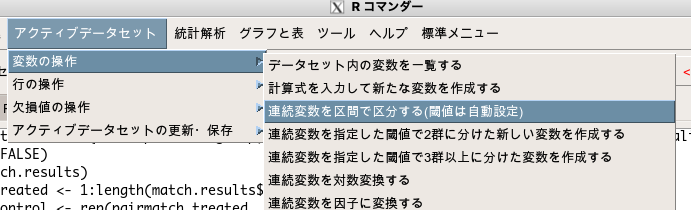
ではEZRでどうすればいいかというと、「アクティブデータセット」→「変数の操作」→「連続変数を区間で区分する」という機能を使います。
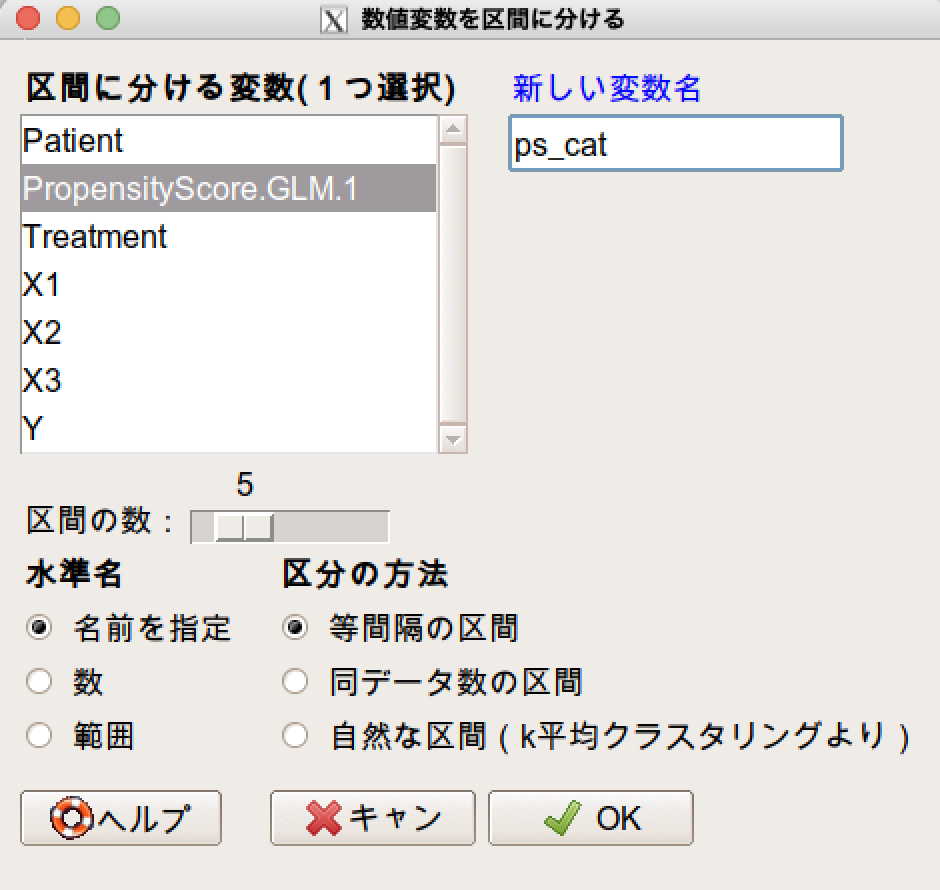
新しい変数名を付与して(今回はps_catとした)、区間の数を決めます(今回は5にしてみる)。
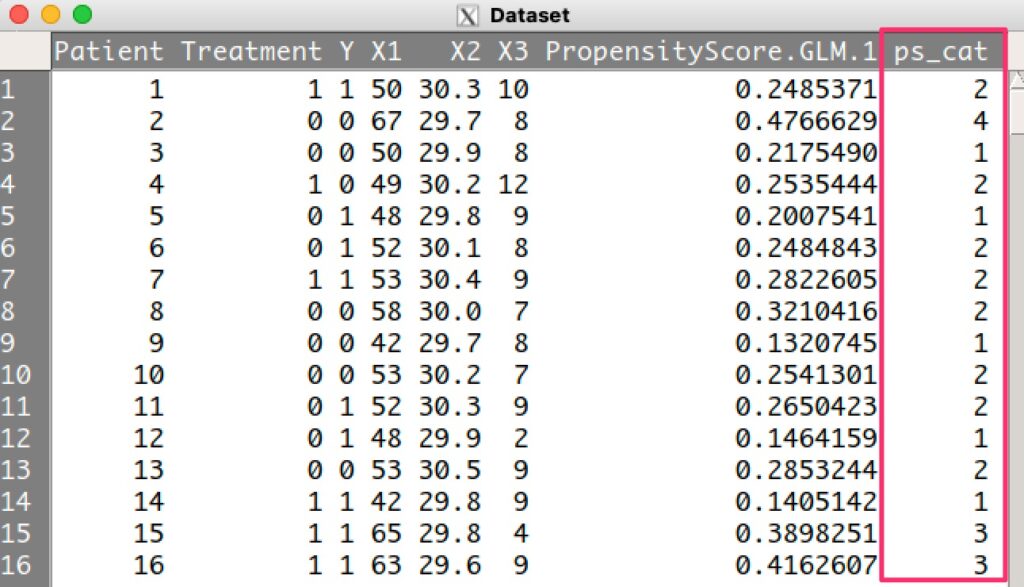
そしてOKを押して、念の為、ps_catが作成されたことを確認します。
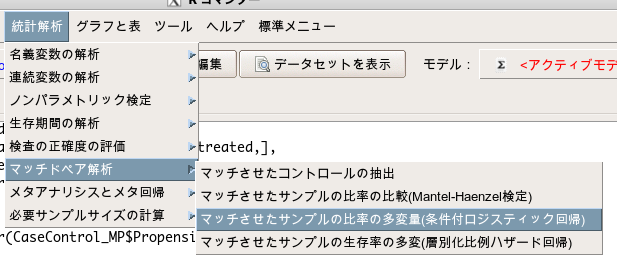
ここまでできたら、条件付きロジスティック回帰分析を実施すればOK。
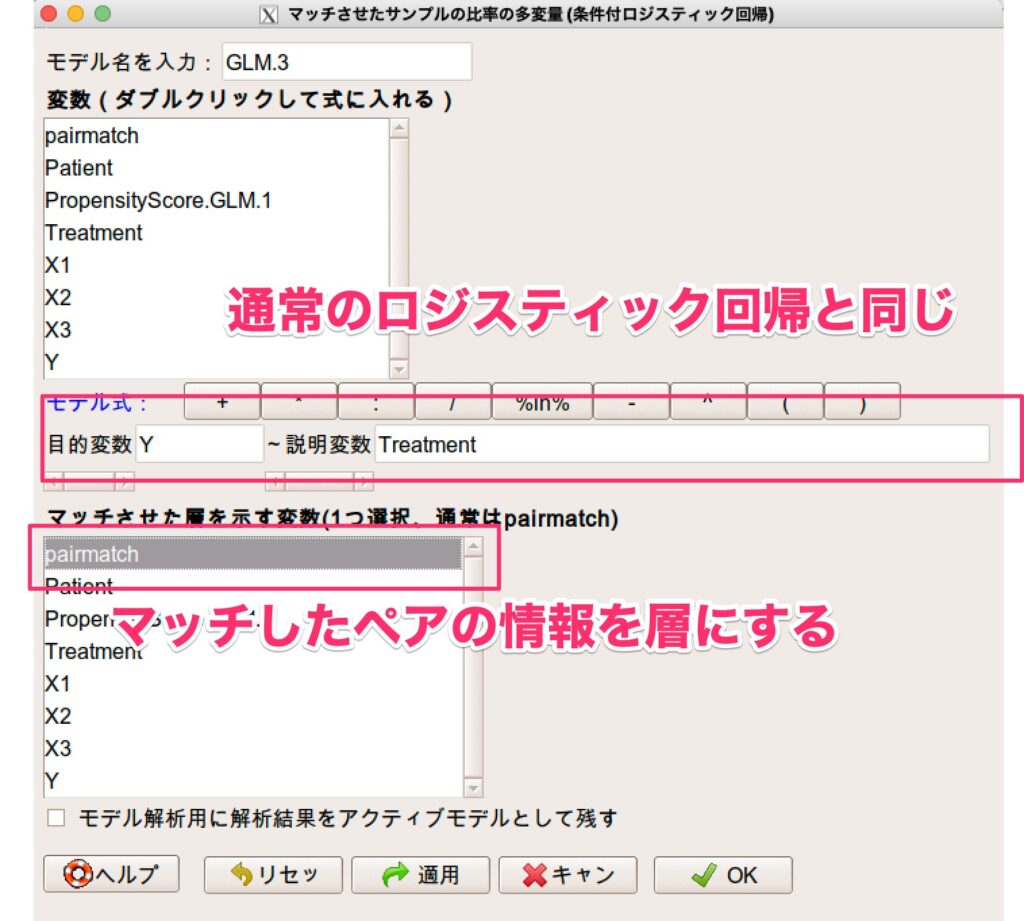
「マッチドペア解析」>「マッチさせたサンプルの比率の多変量(条件付ロジスティック解析)」を選択。
モデル式では通常のロジスティック回帰分析と同じように入力し、マッチさせた層を示す変数に先程作った変数(ps_cat)を選択します。
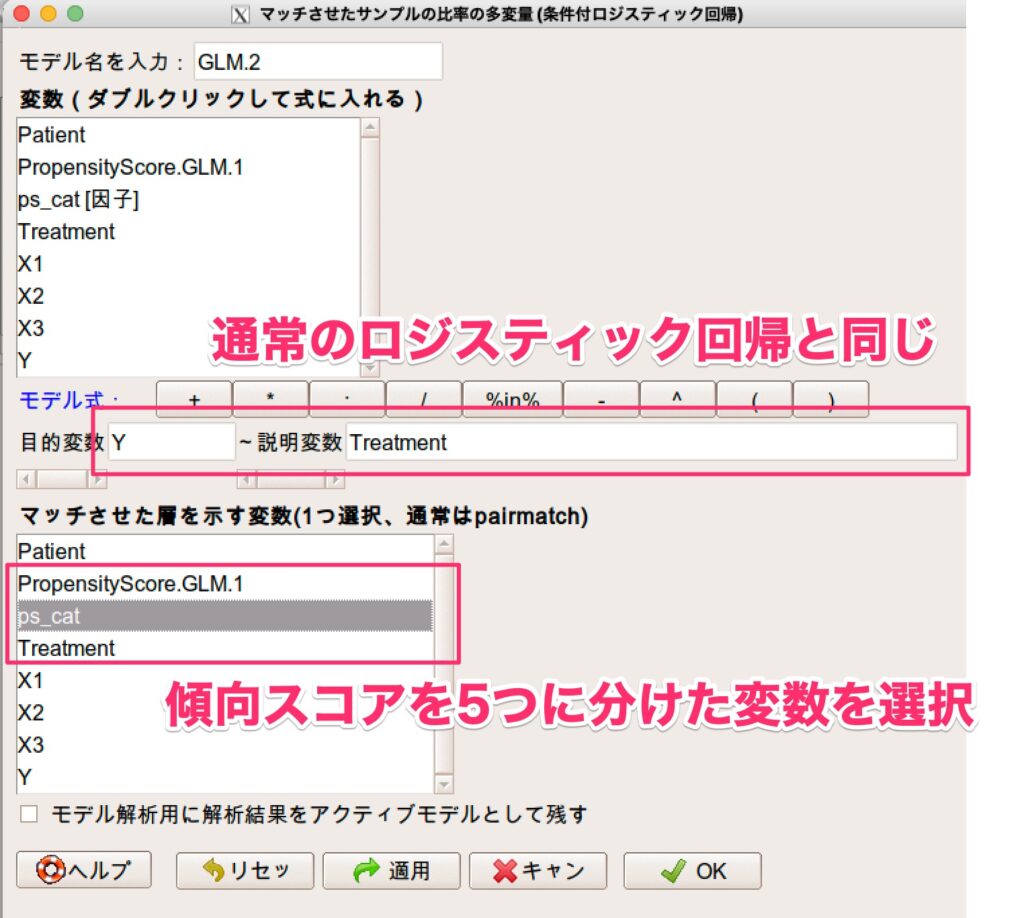
OKを押すと、条件付きロジスティック回帰分析を実施してくれて、結果も下記のように出力されます。

上記で説明させていただいたとおり、オッズ比は一つだけ出力され、通常のロジスティック回帰と同じように結果は解釈します。
傾向スコアマッチングを実施し、マッチング情報を元にして条件付きロジスティック回帰分析を実施する
次に、傾向スコアマッチングを実施し、マッチング情報を元にして条件付きロジスティック回帰分析を実施する方法について解説します。
上記で作成した傾向スコアを元に、まずはマッチングします。
「マッチドペア解析」>「マッチさせたコントロールの抽出」を選択。
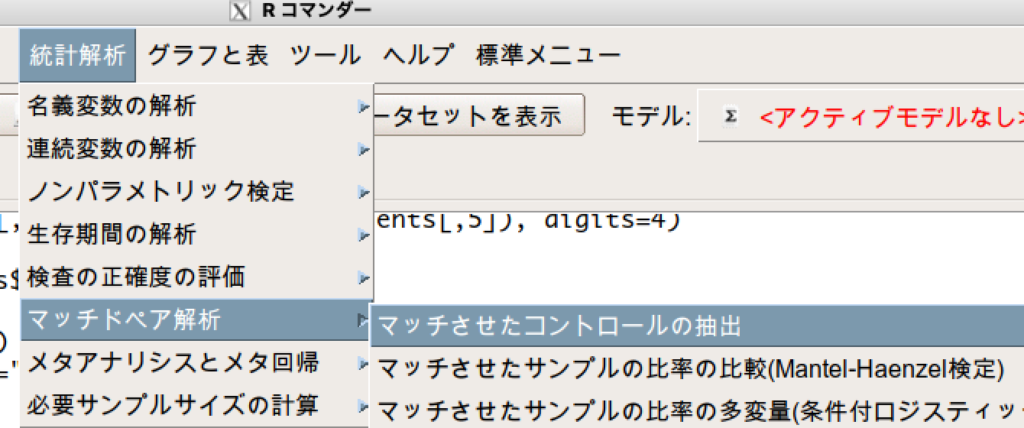
比較する群の変数にTreatment、マッチさせる変数に傾向スコアを選択します。
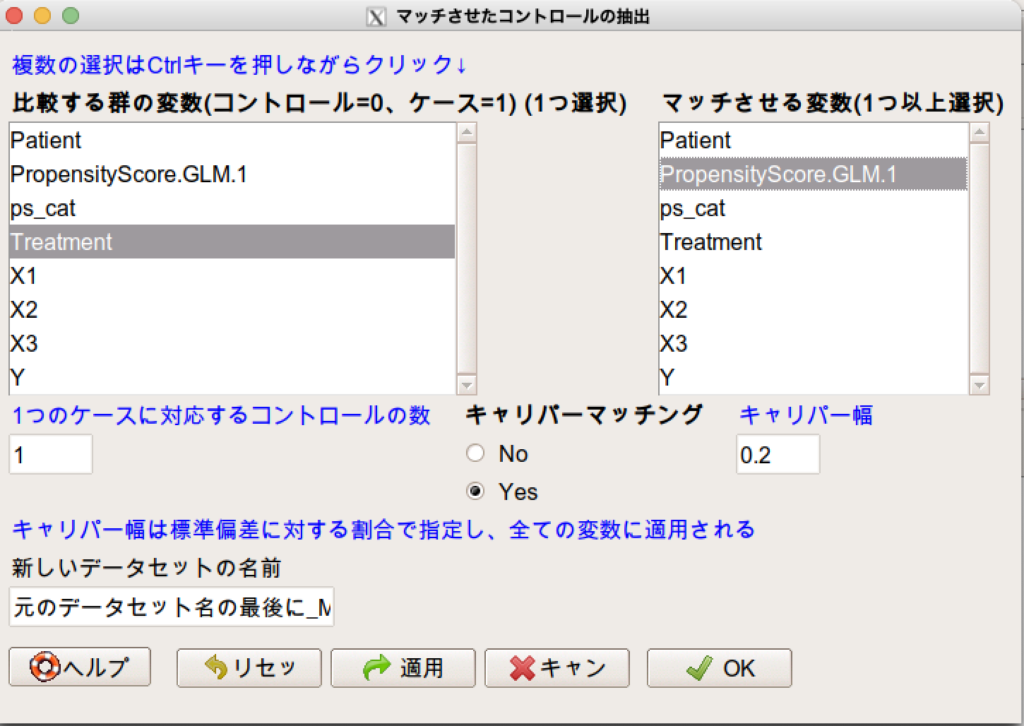
そうすると、マッチングした際のペアの情報が付与されます。
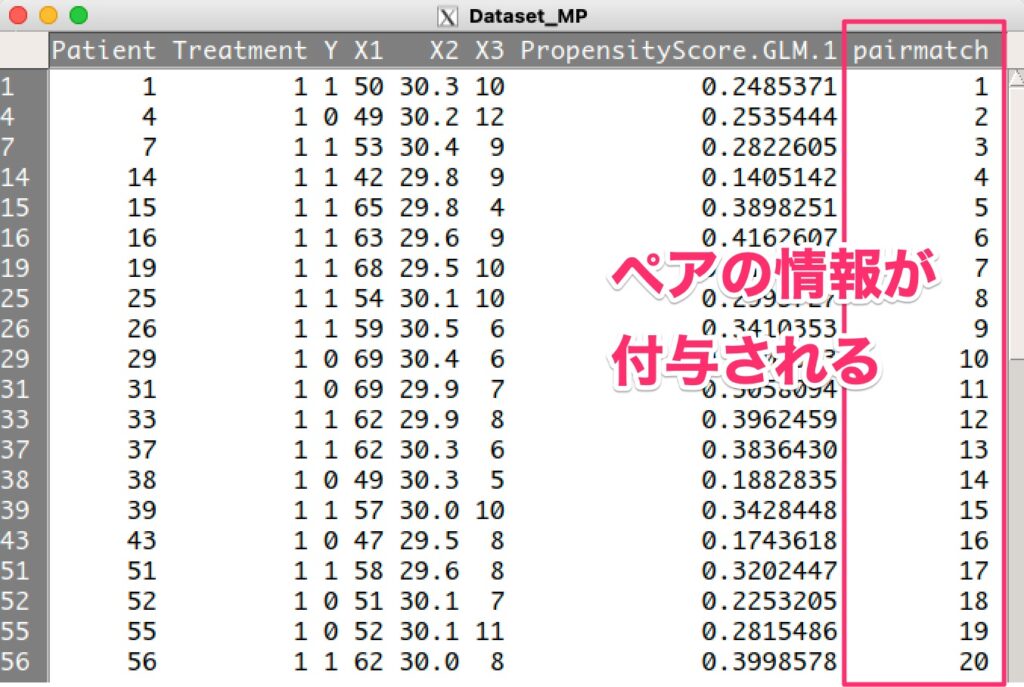
このペアの情報を元にして、条件付きロジスティック回帰分析を実施します。
OKを押すと、条件付きロジスティック回帰分析を実施してくれて、結果も下記のように出力されます。

SPSSで条件付きロジスティック回帰を実施する方法
では次に、SPSSで条件付きロジスティック回帰分析を実施してみます。
状況としては、傾向スコアマッチング実施した後に条件付きロジスティック回帰を実施してみる、という状況です。
傾向スコアを算出して傾向スコアを3〜5つの層に分ける方法は、スキップします。
今回はEZRで作成した傾向スコアマッチングの情報を使います。
実は、SPSSでは条件付きロジスティック回帰分析を実施する選択肢がなく、実は生存時間解析の枠組みを用いて条件付きロジスティック回帰を実施します。
そのため、データの準備としてY=1のときにY2=1、Y=0のときにY2=2、となる変数Y2を作成します。
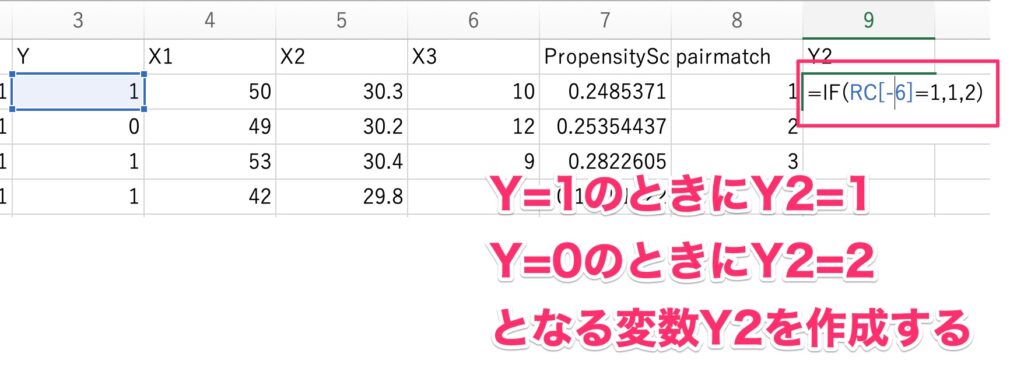
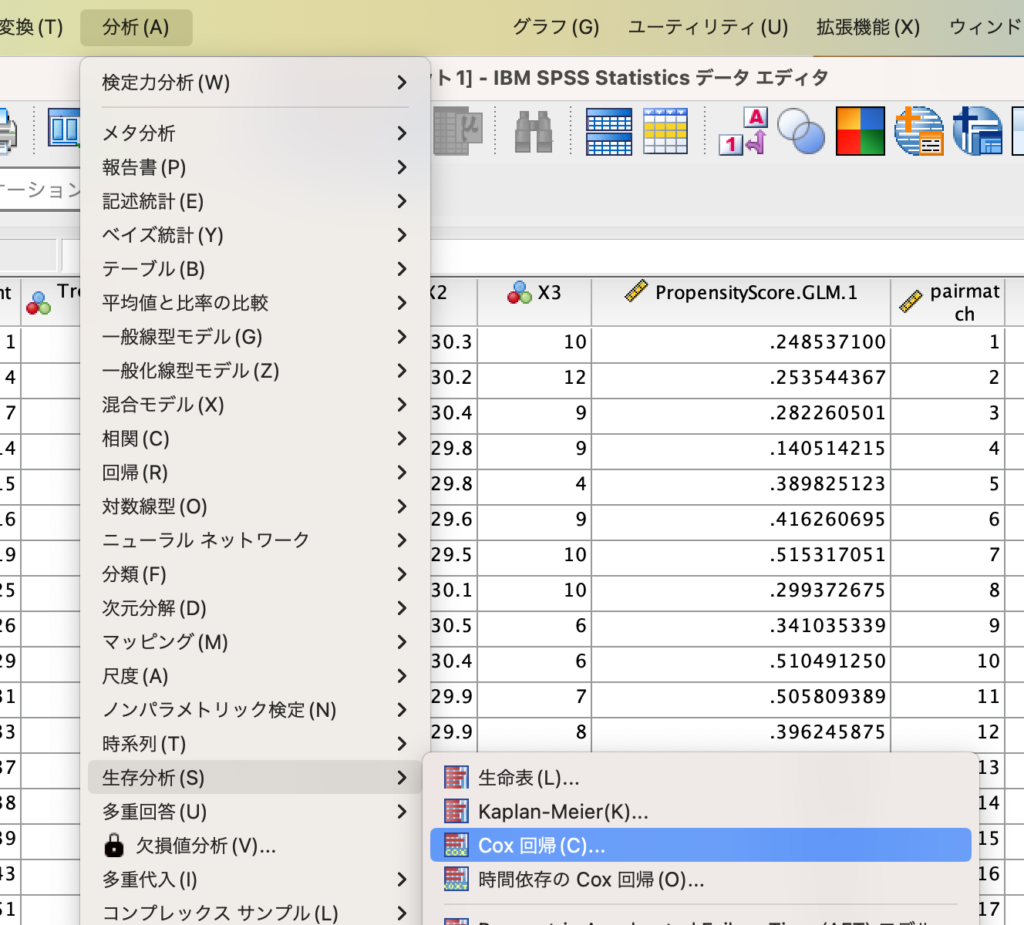
このデータをSPSSに読み込み、「分析」→「生存分析」→「Cox回帰」を選択します。
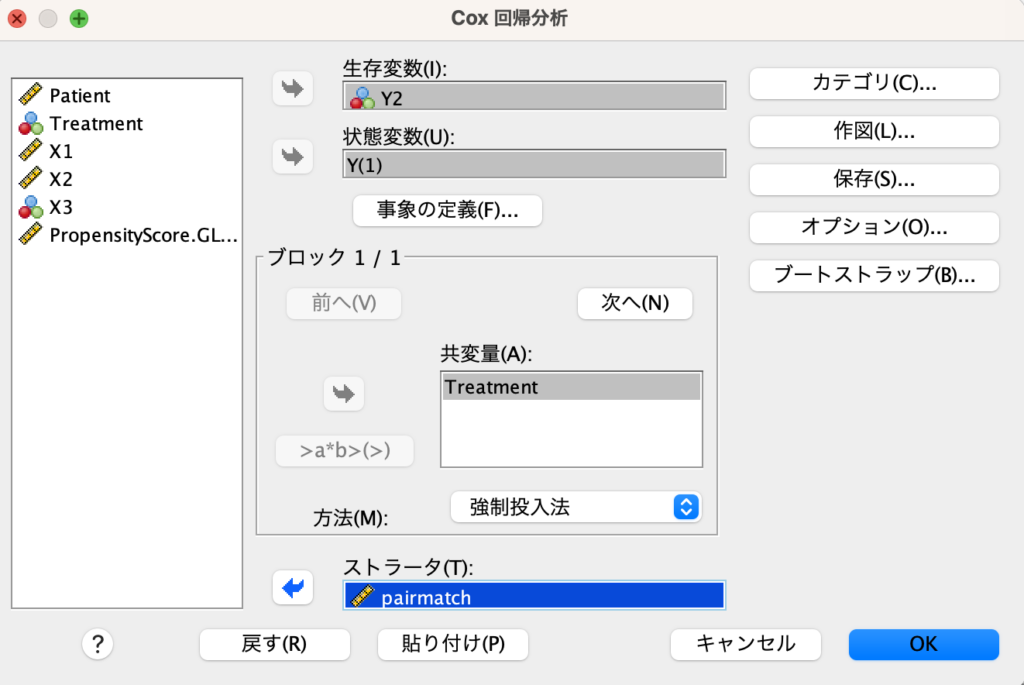
下記のように変数を選択します。
- 「生存変数」としてY2
- 「状態変数」としてY
- 「共変量」としてTreatment(群)
- 「ストラータ」としてpairmatch(傾向スコアマッチングのペア情報)
「オプション」をクリックして、「expに関するCI」にチェックを入れます。このチェックにより、オッズ比に対する95%信頼区間を出力してくれます。
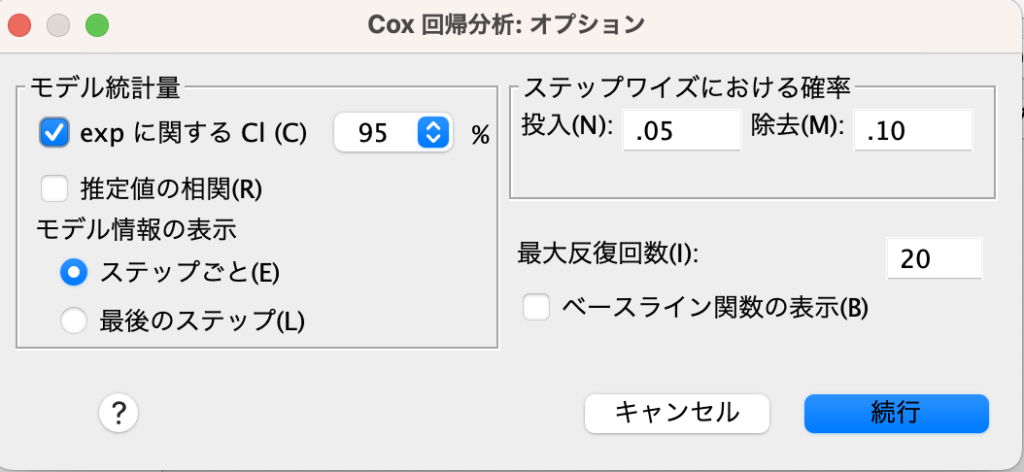
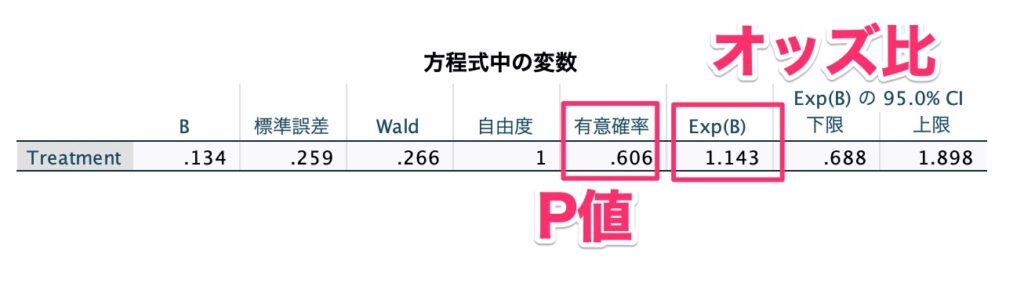
そうすると、下記の通りオッズ比が1.143であり、P値が0.606という結果が得られました。
EZRとSPSSの結果が異なるのはなぜか?
EZRとSPSSの条件付きロジスティック回帰の結果を併記すると、下記のようになります。
| オッズ比 | P値 | |
|---|---|---|
| EZR | 1.36 | 0.435 |
| SPSS | 1.143 | 0.606 |
なぜこのような結果の違いが出ているかというと、ソフトウェアの標準設定(デフォルト設定)が異なるためです。
EZRの標準は、正確法 (Exact Method)です。
理論上、最も正確な確率を計算する手法です。すべての可能な組み合わせを考慮するため、特にペアの人数が多いと計算に時間がかかる場合がありますが、最も厳密な結果が得られます。
一方のSPSSの標準はBreslow法 (Breslow’s Method)です。
正確法の計算を簡略化した、実用的な「近似法」です。計算が非常に高速であり、広く採用されています。
試しに、EZRでBreslow法を実施してみます。
下記のようにプログラムを実施してみます。
res <- coxph(Surv(rep(1, nrow(Dataset_MP)), Y) ~ Treatment + strata(pairmatch),
data = Dataset_MP, method = "breslow")
print(res)すると、下記のような結果が得られ、SPSSの結果と同じであることが確認できました。

どちらも統計学的に確立された正しい分析手法であり、優劣ではなく、厳密性を優先するか、計算速度と実用性を優先するかの設計思想の違いです。
SPSSで条件付きロジスティック回帰を実施するのになぜCox回帰の機能を使えるのか?
実は、「条件付きロジスティック回帰」の計算は、「データを特殊な形式にした層別Cox比例ハザードモデル」の計算と数学的に同じだからです。
そのため、SPSSではCox回帰の機能を用いて条件付きロジスティック回帰を実施します。
EZRでも、Breslowの方法を用いる場合には、coxph()関数を用いることによって条件付きロジスティック回帰を再現可能になります。
ちなみに、EZR(R)にはclogit()という条件付きロジスティック回帰専用の関数がありますが、実はこのclogit()関数の内部では、データを上記のように自動で変換してcoxph()を呼び出しているだけ、という実装になっています。
まとめ
いかがでしたか?
この記事では「条件付きロジスティック回帰分析とは?傾向スコアマッチング後にも使う解析」ということでお伝えしました。
もしあなたが傾向スコアを使った論文を考えているのであれば、ぜひお役立てください!
参考書籍:SPSSによるロジスティック回帰分析















コメント