主成分分析（PCA; Principal Component Analysis）は、複数の変数における変動をできるだけ説明する、少数の独立した線形結合（主成分）を求める解析手法。
例えば、体重と身長という2つの変数がある場合に、BMIという1つの変数に縮小させる、というようなイメージですね。
この記事では、統計解析ソフトJMPを用いた、主成分分析のやり方に関して説明していきます。
JMPで主成分分析をする前にちょっとだけ復習！
主成分分析（PCA; Principal Component Analysis）は、複数の変数における変動をできるだけ説明する、少数の独立した線形結合（主成分）を求める解析手法。
ですが注意点としては、主成分分析自体は「少数の変数に縮小させる」という目的だけであり、縮小させた変数をどう使うかはまた別問題である、ということ。
そのため、主成分分析をした後に何を知りたいのか？という目的が明確ではないと、主成分分析をした後の結果の解釈ができなくなります。
この記事では、JMPで主成分分析を実施する方法までを解説して、主成分分析をした後にどんなことをすべきか？というのは対象外になります！
JMPで主成分分析を実施する！
それでは実際に、JMPで主成分分析を実施していきましょう。
データはJMPにあるサンプルデータを使っていきます。
「ヘルプ」＞「サンプルデータライブラリ」をクリックしていきます。
そして検索画面で「Solubility」を検索すると、「Solubility.jmp」というデータが表示されますので、このデータを開きます。
開いたデータはこのようになっていて、72行7列のデータであることがわかります。
本来であれば、単位が違うデータを主成分分析する場合、標準化しておく必要があります。
標準化とは、データを平均0、分散（標準偏差）1にするということです。
標準化自体は簡単で、各データの値に対して「（データの値-平均値）/標準偏差」という計算をすればいいだけ。
今回のデータは既に標準化されているデータですので、このまま多変量解析を実施していきましょう。
JMPで主成分分析は「分析」＞「多変量」から実施する
データが準備できましたので、実際にJMPで主成分分析を実施していきましょう！
JMPで主成分分析を実施するには「分析」＞「多変量」＞「主成分分析」を選んでいきます。
そして、連続尺度のデータをY,列に選択し、推定法はデフォルトのままにしておきます。
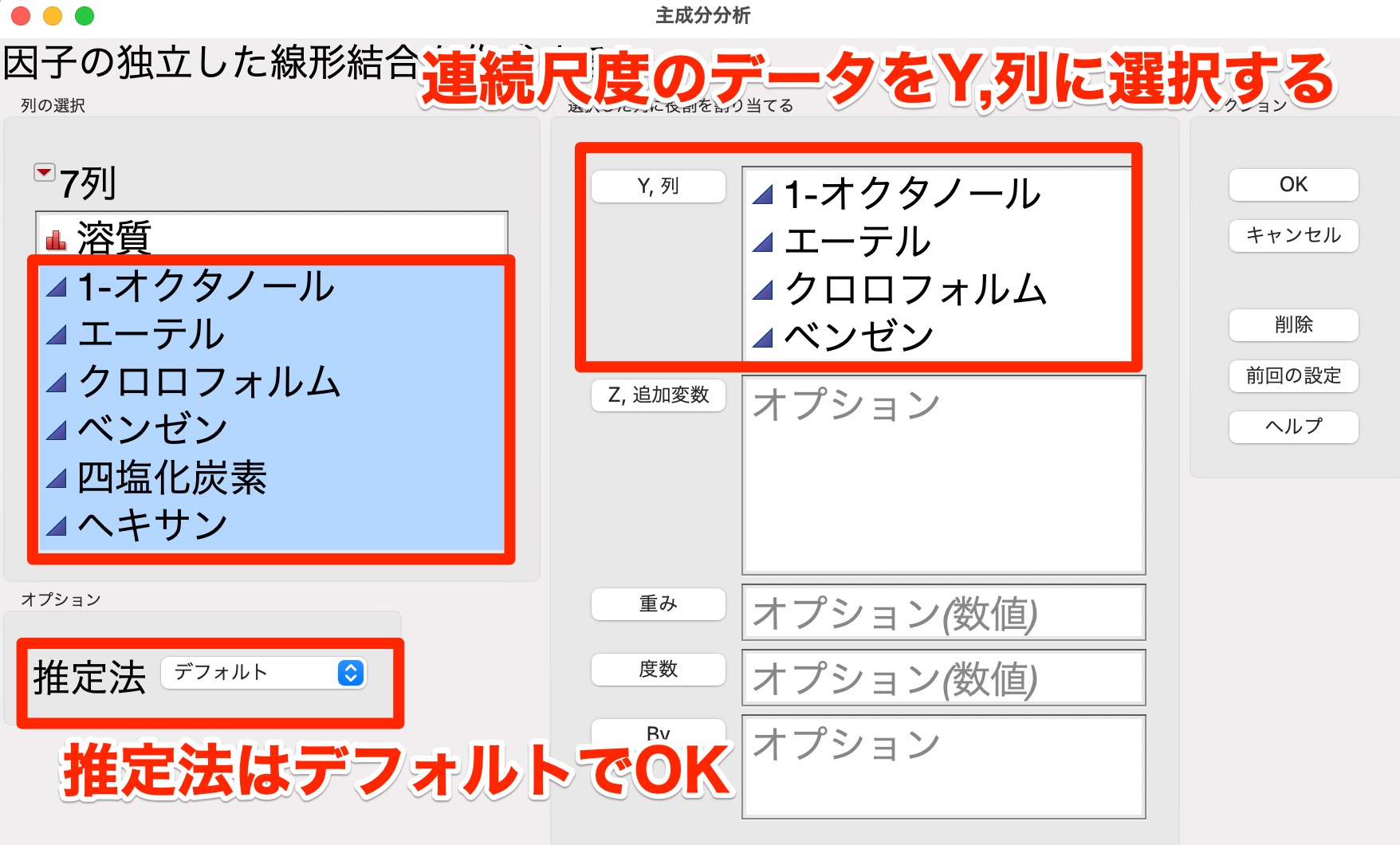
すると下記の通り、主成分分析の結果が出力されました。
JMPで実施した主成分分析の結果を解釈する
JMPで主成分分析を実施すると、下記のような結果が出力されます。
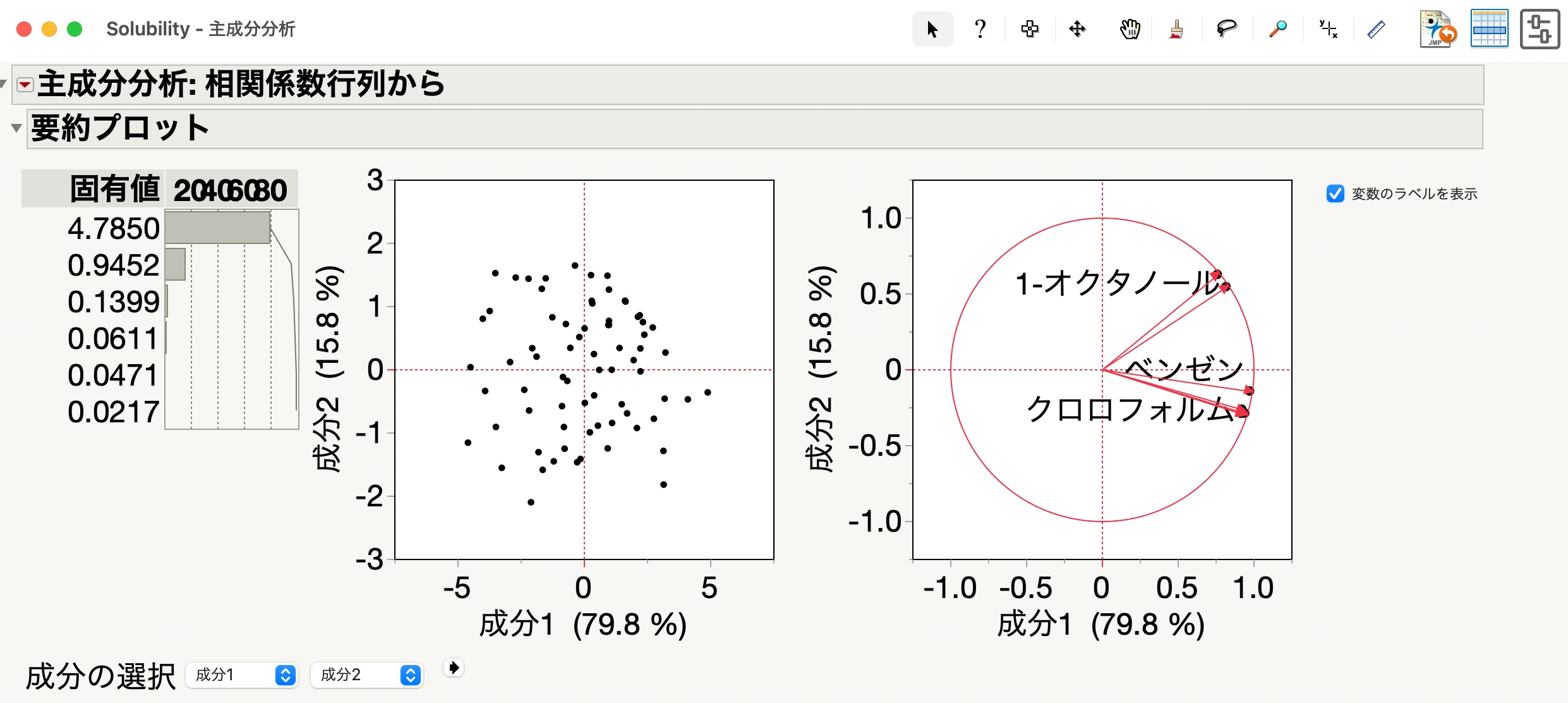
それぞれどのような結果を示しているのかというと、下記の通り。
- 左：固有値と各主成分によって説明される変動の割合を示す棒グラフ
- 真ん中：主成分スコアのプロット
- 右：主成分負荷量のプロット
それぞれ詳しく見ていきます
JMPで主成分分析をした結果の見方：固有値と寄与率
まずは左側に出力されている、固有値と各主成分によって説明される変動の割合を示す棒グラフ。
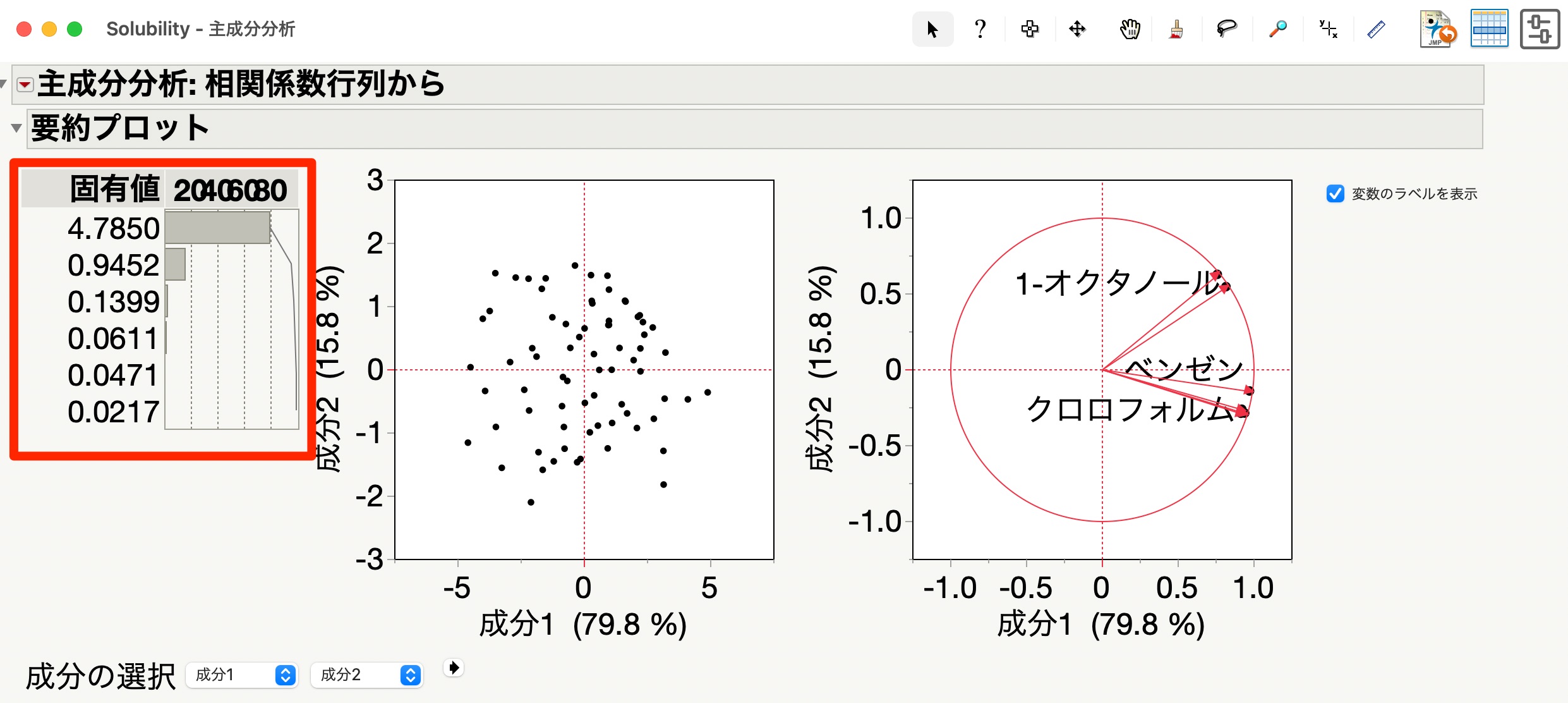
主成分分析において固有値とは、主成分の分散のことを指します。
そして、各主成分によって説明される変動の割合を示す棒グラフのことを寄与率と呼んでいて、対象とする主成分に、元データの情報がどれだけ反映されているかを表した数値のことです。
主成分分析を実施するにあたっては、寄与率を足し合わせた累積寄与率が70%か80％程度以上あれば良いとされています。
そのため、今回の結果では第一主成分で79.8%あり第二主成分で15.8%あるため、第二主成分までの累積寄与率は95.6%あるといえます。
第二主成分までで、かなりの情報量が入っているということが言えますね。
JMPで主成分分析をした結果の見方：主成分スコアのプロット
次に、真ん中の主成分スコアのプロットを見ていきます。
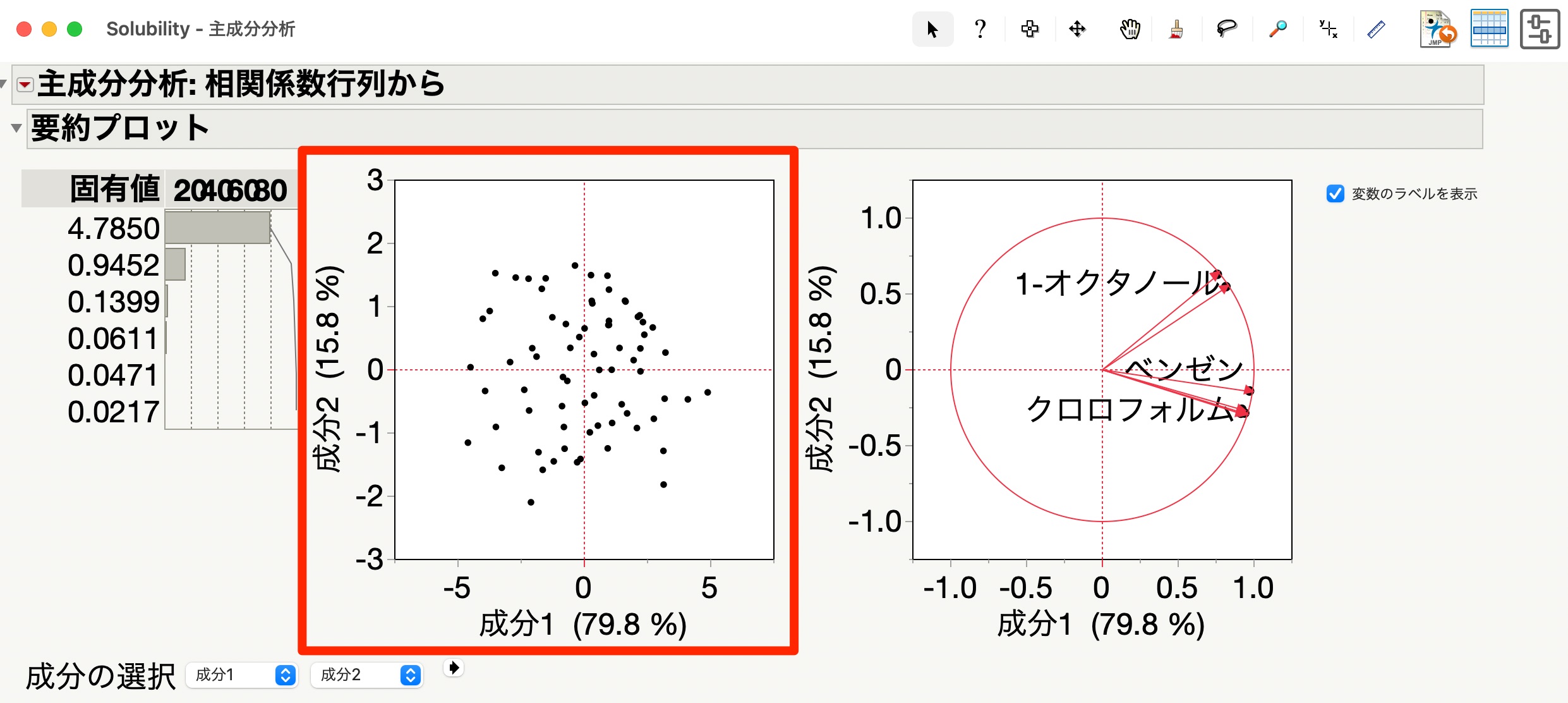
主成分スコアのプロットは、初めの第二主成分までの主成分スコアをプロットしたものです。
相関係数行列に対する主成分分析では、主成分スコアの平均は0で、分散は固有値となっています。
つまり、第一主成分を示しているX軸は平均0、分散4.785である正規分布、第二主成分を示しているY軸は、平均0、分散0.9452である正規分布を示しているということです。
JMPで主成分分析をした結果の見方：主成分負荷量のプロット
次に、右の主成分負荷量のプロットを見ていきます。
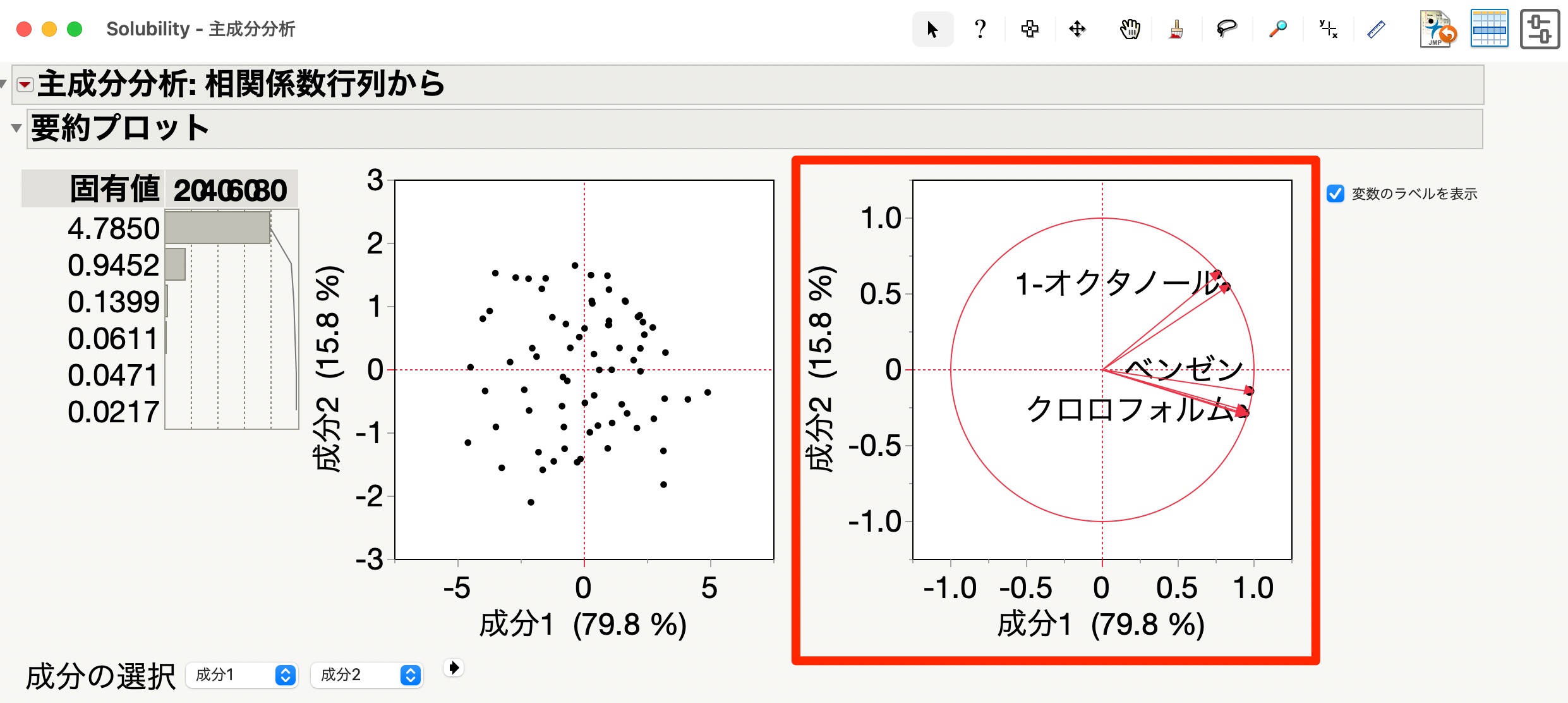
主成分負荷量のプロットは、回転前の主成分負荷量をプロットしたもの。
主成分負荷量は、主成分スコアと各変数との相関を示しています。
そのため、主成分負荷量の絶対値が1に近いほど、主成分スコアと変数との間には強い相関関係があることを示します。
この主成分負荷量を数値として確認したい場合には、左上の赤い三角形を押し、「負荷量行列」をクリックします。
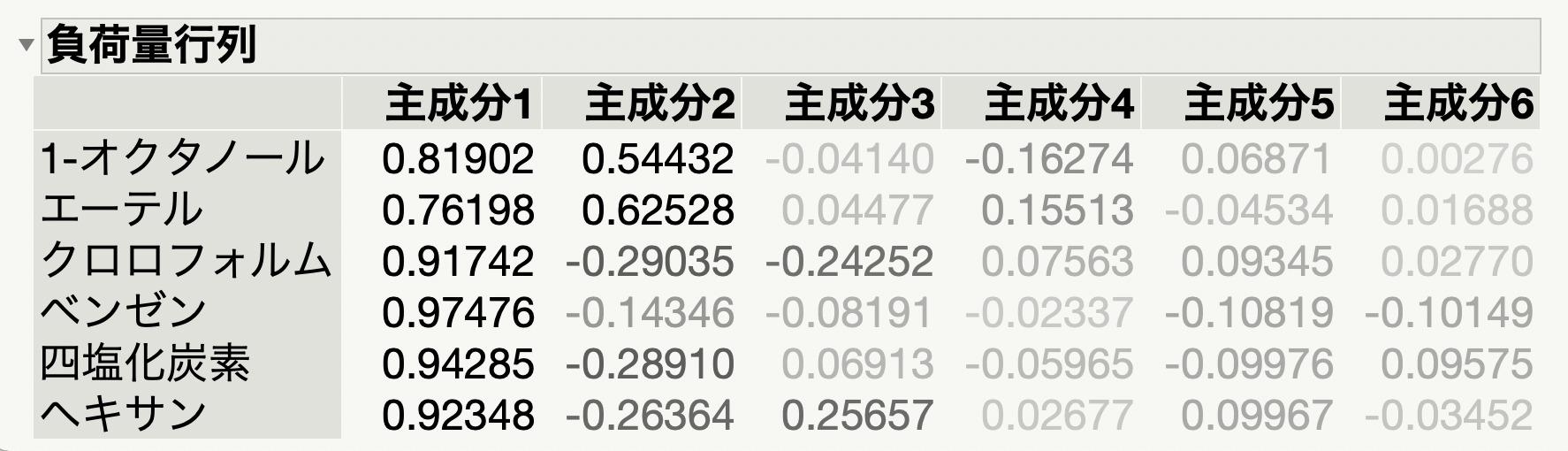
すると下記のように、元のデータの各変数と、各主成分との相関が示されます。
今回のデータでは、第一主成分と各変数との相関がかなり高いことがわかりますね。
まとめ
今回の記事ではJMPで主成分分析を実施する方法についてお伝えしました。
今回の記事で紹介しきれませんでしたが、JMPでは結果が出力された後の左上の赤い三角形を押すことで、かなり詳細な結果を確認することもできます。
ぜひお手元で色々と試してみてください！
コメント