連続量のデータを群間で比較したい。
しかし、そのアウトカムに影響を与える他の因子がある。
このようなときに共分散分析（ANCOVA）を用いますね。
この記事では統計解析ソフトJMPを使った共分散分析の解析方法について説明していきます。
Contents
統計解析ソフトJMPでの共分散分析（ANCOVA）を実施する！
共分散分析は、平均値に影響を及ぼすデータ（共変量）があった時に、その共変量の影響を取り除いて群間を比較することができる統計解析の手法です。
詳しくは
>>>共分散分析とは？論文でも使われるANCOVAをわかりやすい例で！
で説明しています。
また、共分散分析は英語のAnalysis of Co-Variance”訳語であるため、略してANCOVAと表記されることもあります。
JMPで交互作用がある場合とない場合の共分散分析
統計解析ソフトであるJMPを用いると共分散解析が簡単に行うことができます。
本記事では、下記の2つの場合の共分散分析を実施してみます。
- 2群間の傾きが等しい場合の共分散分析（つまり、交互作用がない場合）
- 2群間の傾きが異なる場合の共分散分析（つまり、交互作用がある場合）
この違いを簡単に説明します。
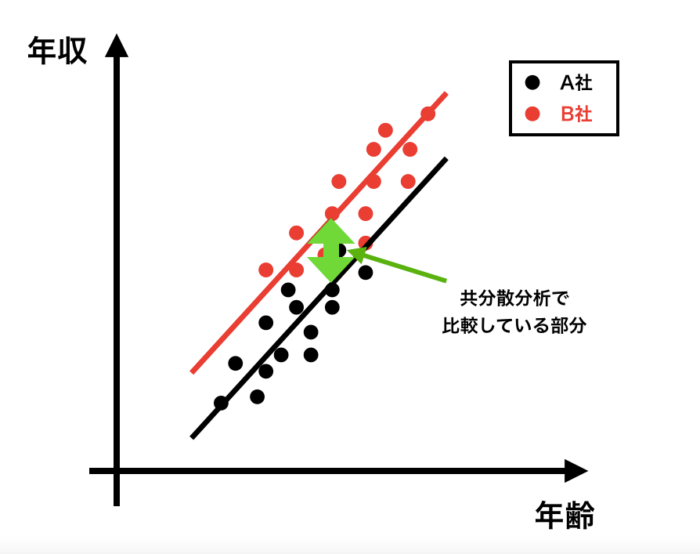
>>>共分散分析とは？論文でも使われるANCOVAをわかりやすい例で！
で紹介した年収と年齢の関係の図です。
この図では黒（A社）と赤（B社）の回帰線が引かれていて、2本の線は平行しています。
このように2本の回帰直線の傾きが等しいとき、”交互作用がない場合の共分散分析”を用います。
一方で、この回帰直線の傾きが異なるとき、”交互作用がある場合の共分散分析”を検討します。
ただ、実際の研究では、ほとんどの場合「交互作用がない場合」の共分散分析を実施することが多いです。
JMPで共分散分析（ANOVA）を実施する（交互作用がない場合）
では早速、”交互作用がない場合の共分散分析”のやり方を説明していきます。
JMPへデータの読み込み
自分たちのデータを解析する場合は、[ファイル] > [開く]から解析したデータを開いてください。
ExcelやCSV形式のデータを開くことができます。
この記事では、JMPにすでに用意されているサンプルデータを使います。
[ヘルプ] > [サンプルライブラリー]をクリックします。
すると、次のサンプルデータのディレクトリのウィンドウが出てきます。
今回はこの中の”Drug.jmp”を使います。
このデータは”薬剤を投与した時の、投与前と投与後のある値を測定したとき”のものです。
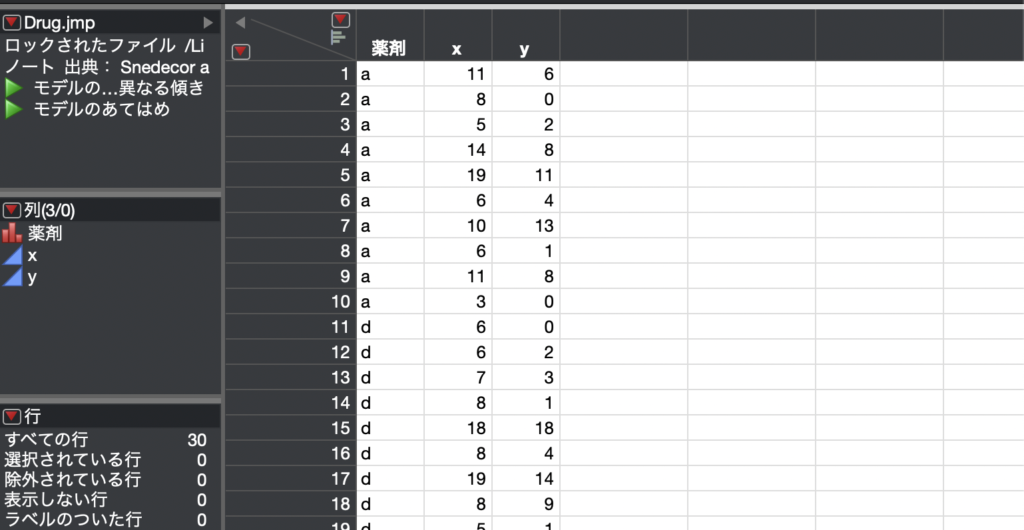
「薬剤」の項目が摂取した薬剤を、
「x」が摂取前の値を、
「y」が摂取後の値を表しています。
このデータから、摂取前の値が影響するときに、本来の薬剤の効果を共分散分析を用いて調べてみます。
JMPで共分散分析を実施
共分散分析を行うには、[分析] > [モデルのあてはめ]をクリックします。
すると下のウィンドウが出現します。
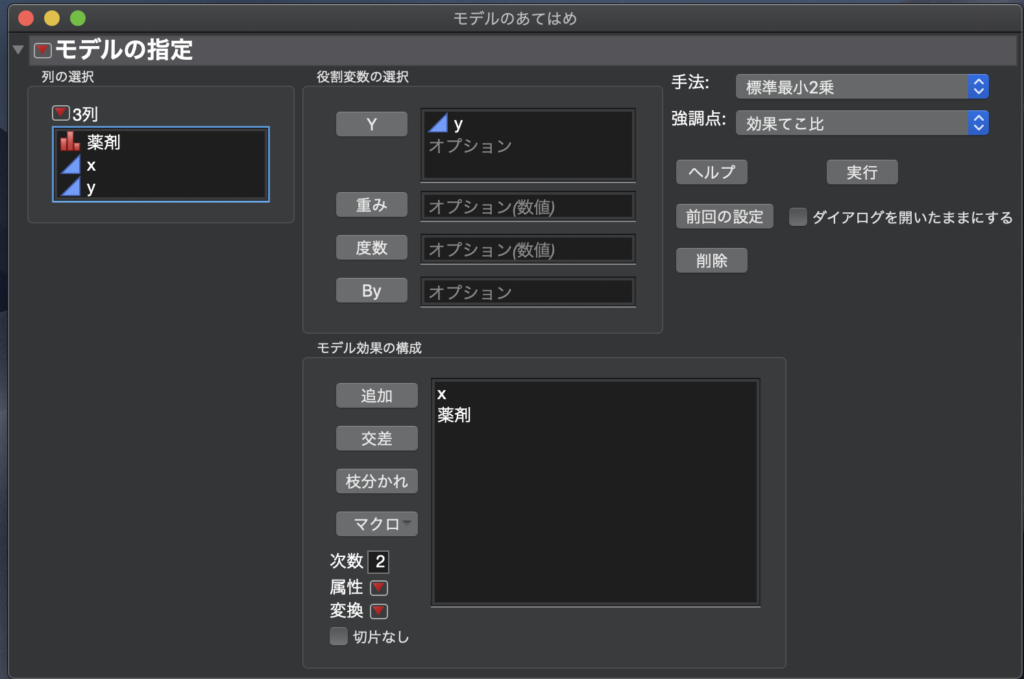
[Y]の項目に「y」の列を、[モデル効果の構成]には「x」と「薬剤」を追加します。
追加ができたら[実行]をクリックします。
クリックすると、共分散分析の結果が出力されます。
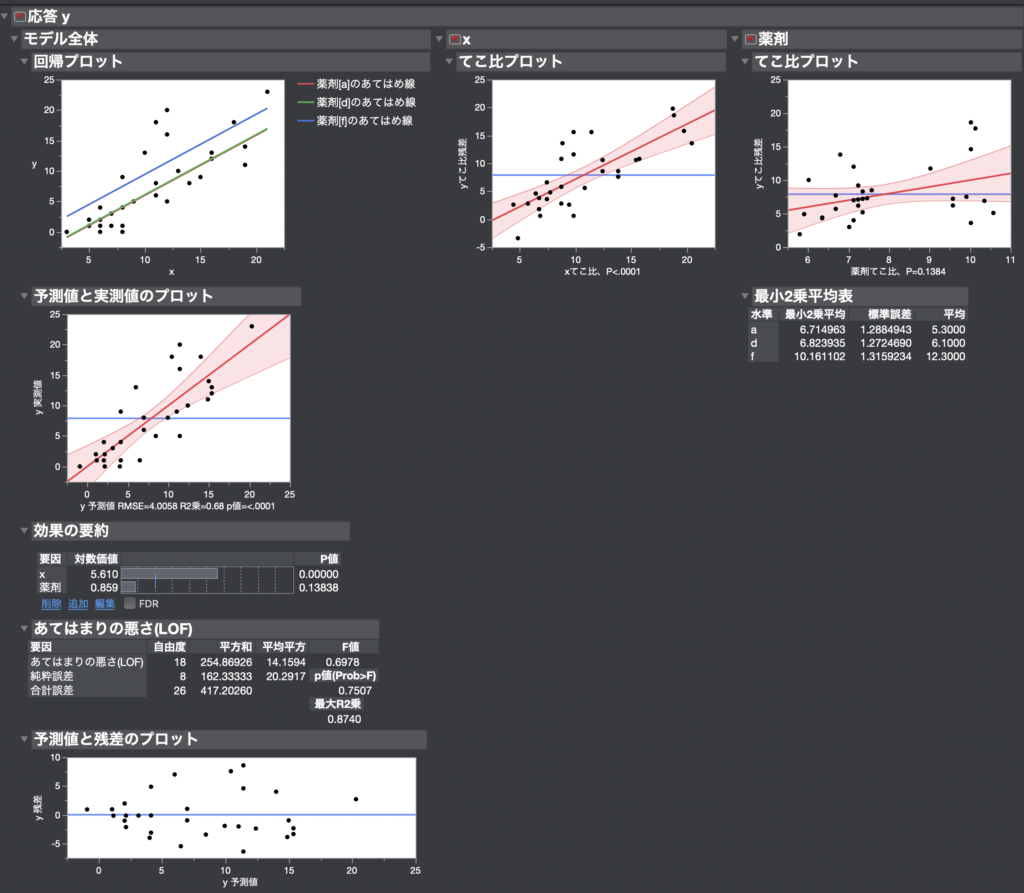
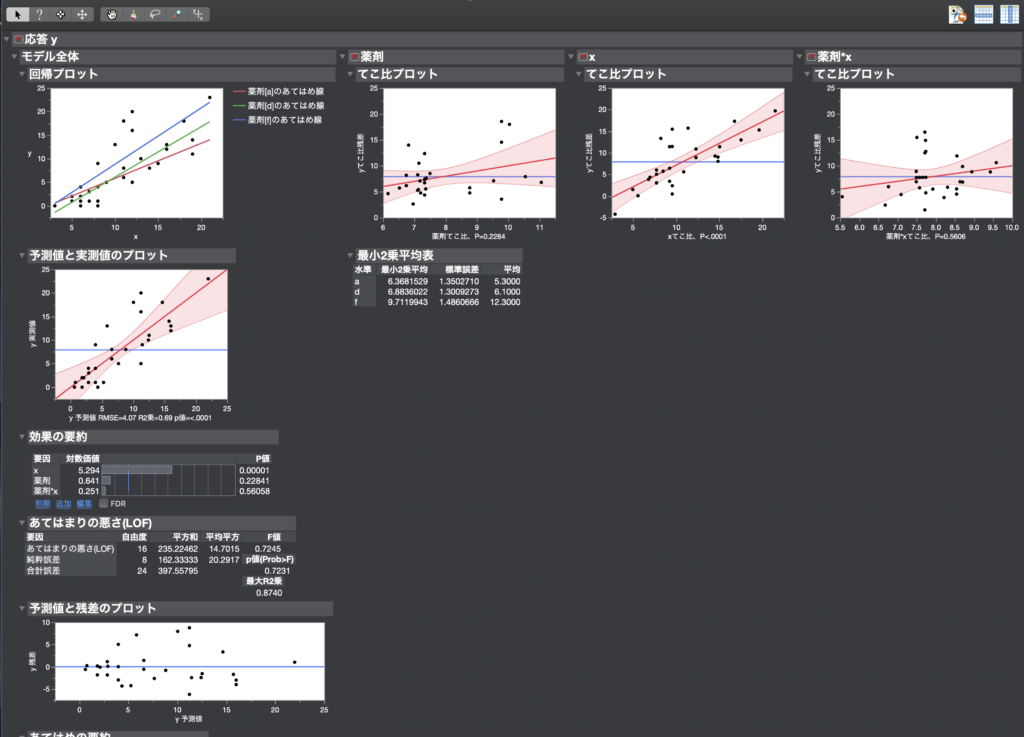
左上に回帰プロットが描かれています。
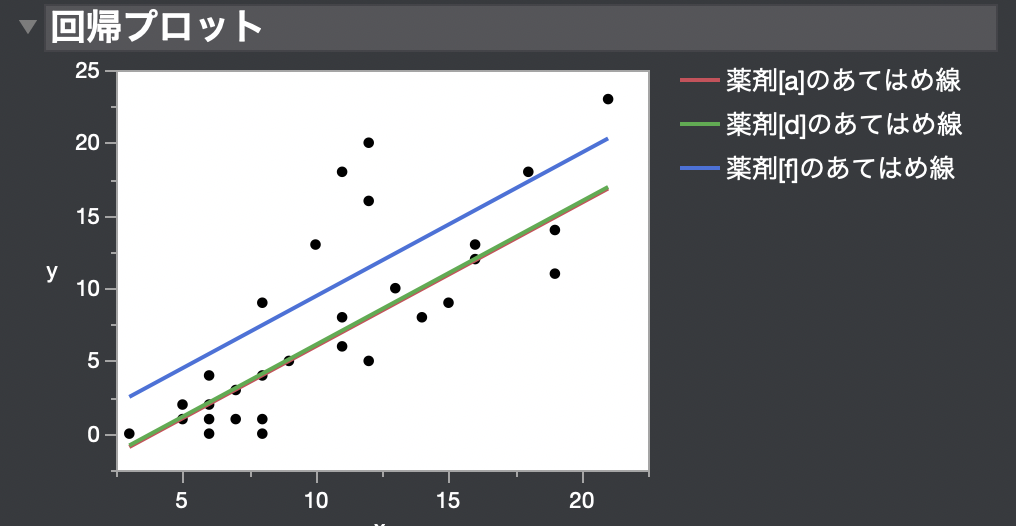
ここで、線が平行なのは、傾きが等しい場合の共分散分析として解析を行っているからです。
傾きが大きく違う時は、統計解析結果が正しくない可能性が大きくなってしまします。
今回の共分散分析の結果は、一番下の[検定の効果]を見たらわかります。
この結果からわかることは、「薬剤」という要因はP=0.1384と有意水準を満たさないため、”薬剤による効果の差があるとは言えない”ことを意味します。
ちなみに、てこ比プロットに関しましては、JMP事業部のこちらの解説をご覧いただければと思います。
https://www.jmp.com/support/help/ja/16.2/index.shtml#page/jmp/leverage-plots.shtml
JMPで交互作用がある場合の共分散分析（ANCOVA）
“交互作用がある場合の共分散分析”のやり方を説明していきます。
JMPで交互作用がある場合の共分散分析を実施すrう
途中までは基本的に同じです。
[分析] > [モデルのあてはめ]をクリックします。
[Y]の項目に「y」の列を選択します。
以上までは「交互作用がない場合の共分散分析」と同じですが、ここからが異なります。
「x」と「薬剤」を選択します。
[モデル効果の構成]にある[マクロ]をクリックし、[設定された次数まで]を選択します。
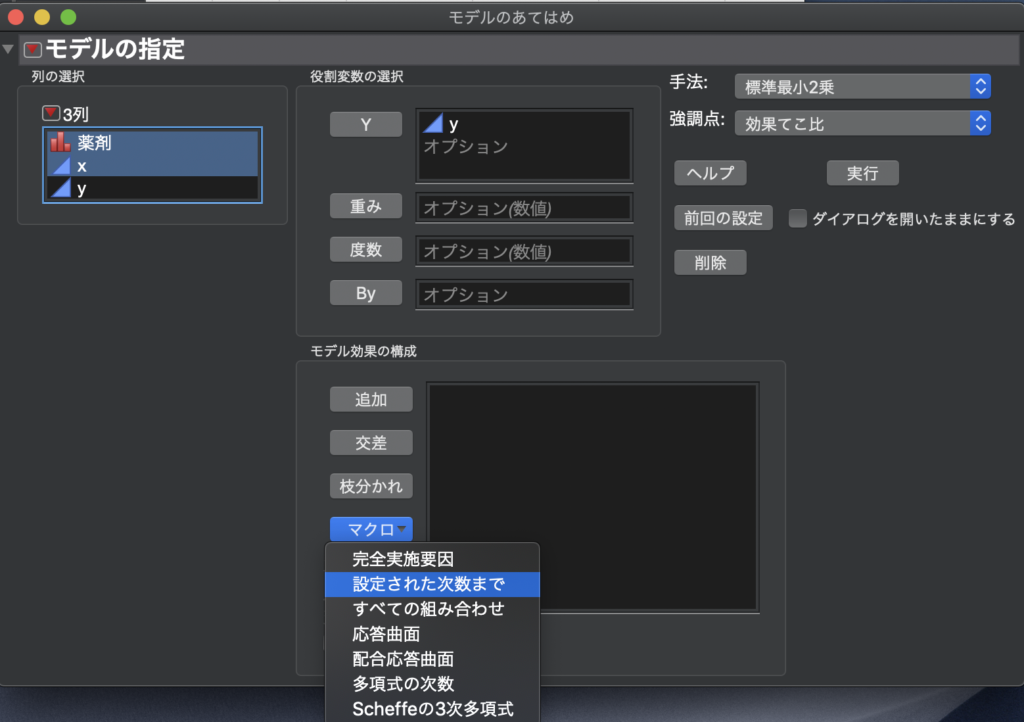
デフォルトの次数は2です。
今回はこのままで行います。
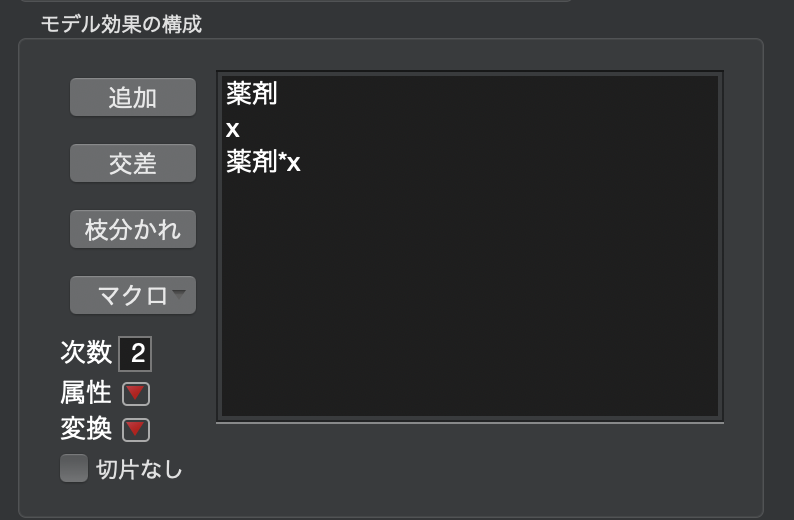
すると、[モデルの効果に]、「薬剤」、「x」に加えて、「薬剤*x」という項目が追加されます。
薬剤*xは交互作用項といいます。
交互作用は“2つの因子が合わさって現れる相乗効果（もしくは拮抗効果）”のことです。
最後に、[実行]をクリックします。
これで、共分散分析の結果が出力されます。
傾きが異なるので、回帰プロットも傾いた形になっています。
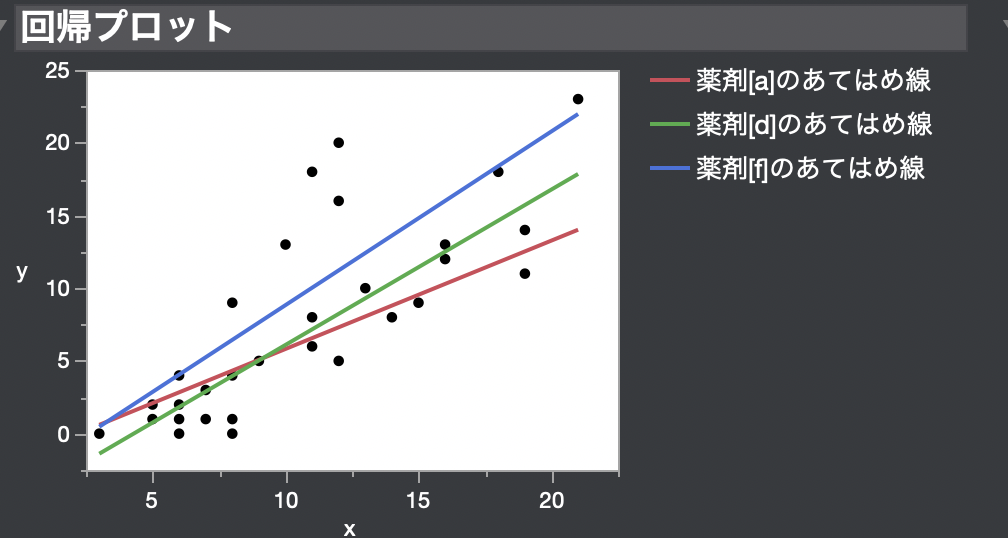
傾きが等しい場合の共分散分析とはモデルが異なるため、
結果も違います。
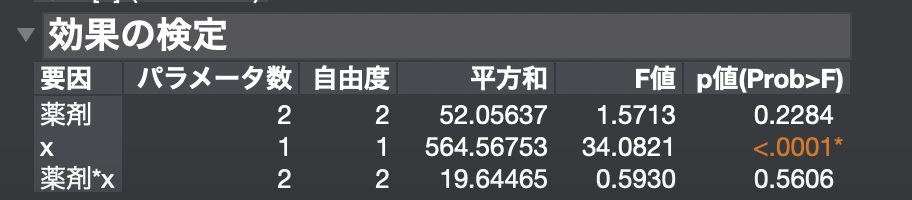
「薬剤」も「薬剤*x」の効果も有意差はありません。
JMPで共分散分析（ANCOVA）をする方法まとめ
- JMPには傾きが等しい場合の共分散分析と傾きが異なる場合の共分散分析がある
- どちらを使えば良いのかわからない時は”傾きの違い”を検定する
- これらの操作は全て[分析] > [モデルのあてはめ]から行う
株式会社データシードは、SAS社のJMP事業部と提携しています。
統計解析担当者として10年間色々な統計解析ソフトを試した結果、本当に使いやすいと思ったのがJMPでした。
ぜひあなたもJMPの全機能を30日間試せるトライアル版で、データからさらなる情報を導き出せることを実感してください。
第1章：臨床研究ではなぜ統計が必要なのか？計画することの重要性
第2章：研究目的をどれだけ明確にできるのかが重要
第3章：p値で結果が左右される時代は終わりました
第4章：多くの人が統計を苦手にする理由
第5章：統計を使えるようになるために今日から何をすれば良いか？
第6章：統計を学ぶために重要な環境
もしあなたがこれまでに、何とか統計をマスターしようと散々苦労し、何冊もの統計の本を読み、セミナーに参加してみたのに、それでも統計が苦手なら…
私からプレゼントする内容は、あなたがずっと待ちわびていたものです。
