この記事では、「JMPでパラメトリックな多重比較!Tukey検定とDunnett検定を実施する方法」ということでお伝えしていきます。
3群以上の比較をしたい時、検定の目的によっては多重性の問題が発生します。
多重性の問題は、統計学的検定を2回以上実施した時点で発生するため、多くの研究で直面する課題です。
多重性の問題を回避するには、大きく分けて3つの方法があります。
- どうにかして検定を1つにする
- 有意水準を分ける・多重性を考慮した検定を用いる
- 検定に順番をつける(閉手順)
この記事では「多重性を考慮した検定を用いる」にフォーカスを当てて解説します!
特にパラメトリックな方法である、Tukey検定とDunnett検定のJMPでの実施方法をお伝えしますね。
多重比較検定の種類は?パラメトリックな方法で有名なTukey検定とDunnett検定

多重性を考慮した検定は多くありますが、ここでは有名な4つの検定手法をご紹介します。
これらは全て、連続量(連続尺度)のデータを解析する検定手法です。
- Tukey検定
- Dunnett検定
- Steel-Dwass検定
- Steel検定
上記4つの手法はどのような違いがあるかというと、下記の表のように分類できます。
| パラメトリック検定 | すべての群との比較をする | Tukey検定 |
| 対象群(コントロール群)との比較だけをする | Dunnett検定 | |
| ノンパラメトリック検定 | すべての群との比較をする | Steel-Dwass検定 |
| 対象群(コントロール群)との比較だけをする | Steel検定 |
今回の記事では、上のパラメトリック検定の2つを紹介します。
表にある通り、Tukey検定とDunnett検定の違いは「比較する群の数」です。
この違いはJMPを操作しながら学んでいきましょう。
上記4つの検定に関して、詳しくはこちらの記事をご覧くださいませ!
>>Post-hoc test(事後検定)とは?なぜ分散分析(ANOVA)の後の多重比較との認識なのか?
JMPで多重比較のTukey検定とDunnett検定を実施する!
では実際にJMPでTukey検定とDunnett検定を実施していきましょう。
JMPで多重比較1:多重性を考慮しない多重検定(Studentのt検定)を実施する
多重性を考慮した検定に関してお伝えする前に、多重性を考慮した検定結果とどれ程異なるかを比較するため、多重性を考慮しない検定結果(Studentのt検定の結果)をみてみたいと思います。。
今回はJMPのサンプルデータである「Analgesics」を使います。
Analgesicsはサンプルデータの「分散分析」の中にあります。
多重性を考慮しない多重検定(Studentのt検定)をJMPで実施する場合には、以下の手順で実施します。
対象となるデータ(今回はAnalgesics)を開いた状態で「分析」>「二変量の関係」を選択。
「X,説明変数」に薬を入れ、「Y,列」に痛みの程度を入れて「OK」を選択。
すると薬剤A,B,Cごとに痛みの程度の値がプロットされる散布図が作成されている。
この散布図の「薬による痛みの程度の一元配置分析」の左側の赤い三角形から「平均の比較」>「各ペア、Studentのt検定」を選択する。
すると、散布図の右側には「比較円」と呼ばれる円が表示され、散布図の下にはStudentのt検定を使った全ペアの比較結果が表示されます。
Studentのt検定では、1番下に全てのペアの対比較(A vs B, B vs C, C vs A)結果がP値とともに表示されています。

以上で、多重性を考慮しない検定結果が表示されました。
多重性を考慮しない検定結果であるため、解釈には注意する必要があります。
今回のデータでは薬剤A,B,Cという3群を比較するため全てのペアは3通りあることになります。
つまり、3回検定を実施していることに相当します。
多重性の問題は「2回以上統計学的検定を実施したとき」に生じる問題ですので、今回の比較でも多重性の問題を考える必要がありますね。
多重性を考えずに全ペアの検定を実施したところ、有意水準0.05としたときには「C vs A」と「B vs A」の2つの検定で有意差がある、という結論になります。
しかし繰り返しになりますが、これは多重性を考慮していない検定結果ですので、本当にこのままの結果を提示して良いかどうかは考える必要があります。
JMPで多重比較2:多重比較検定であるTukey検定を実施する
今度はTukey検定を実施します。
Tukey検定は「パラメトリック検定」であり「全ての群との比較をする」という検定手法でしたね。
Tukey検定でも先ほどと同様にJMPのサンプルデータである「Analgesics」を使います。
Tukey検定をJMPで実施する場合には、以下の手順で実施します。
対象となるデータ(今回はAnalgesics)を開いた状態で「分析」>「二変量の関係」を選択。
「X,説明変数」に薬を入れ、「Y,列」に痛みの程度を入れて「OK」を選択。
すると薬剤A,B,Cごとに痛みの程度の値がプロットされる散布図が作成されている。
この散布図の「薬による痛みの程度の一元配置分析」の左側の赤い三角形から「平均の比較」>「すべてのペア、TukeyのHSD検定」を選択する。
すると、散布図の右側には「比較円」と呼ばれる円が表示され、散布図の下にはTukey検定での比較結果が表示されます。

Tukey検定では、1番下に全てのペアの対比較(A vs B, B vs C, C vs A)結果がP値とともに表示されています。

Tukey検定をJMPで実施する方法は以上です。
Tukey検定の結果は、多重性を考慮しない全てのペアに対するStudent のt検定と同じ形式で表示されます。
注目していただきたいのは、Tukey検定を実施した際に表示される「差の順位レポート」です。
先ほど実施した多重性を考慮しないStudentのt検定と見比べてみると、有意水準を0.05としたときに有意差ありと結論づけられる比較は「C vs A」のみになりました。
多重性を考慮しない場合には「B vs A」も有意差ありでしたが、多重性を考慮すると有意差がなくなりました。
以上のように、多重性を考慮したときには多重性を考慮しない場合に比べて「有意になりにくい」という性質があります。
多重性を考慮した検定は何種類かありますが、すべての検定において「多重性を考慮しない検定に比べると有意になりにくい」という性質がありますので、その点は理解しておきましょう。
JMPで多重比較2:多重比較検定であるDunnett検定を実施する
今度はDunnett検定を実施します。
Dunnett検定は「パラメトリック検定」であり「対照群(コントロール群)との比較だけをする」という検定手法でしたね。
Tukey検定との違いは「全ての群との比較をする」か「対照群(コントロール群)との比較だけをする」かの違いです。
ここでは仮に「薬剤A」を対照群として考えてみます。
「対照群(コントロール群)との比較だけをする」ため、今回の例では「A vs B」「A vs C」の2つの検定だけを実施することになります。
Tukeyでは上記の2つの検定に加えて「B vs C」の検定を実施しましたが、Dunnett検定ではあくまで「「対照群(コントロール群)との比較だけをする」ため、「B vs C」の検定は実施しません。
Dunnett検定をJMPで実施する場合には、以下の手順で実施します。
対象となるデータ(今回はAnalgesics)を開いた状態で「分析」>「二変量の関係」を選択。
「X,説明変数」に薬を入れ、「Y,列」に痛みの程度を入れて「OK」を選択。
すると薬剤A,B,Cごとに痛みの程度の値がプロットされる散布図が作成されている。
この散布図の「薬による痛みの程度の一元配置分析」の左側の赤い三角形から「平均の比較」>「コントロール群との比較、Dunnett検定」を選択する。
どの群をコントロール群とするかを問われますので、Aを選択します。
すると、散布図の右側には「比較円」と呼ばれる円が表示され、散布図の下にはDunnett検定での比較結果が表示されます。
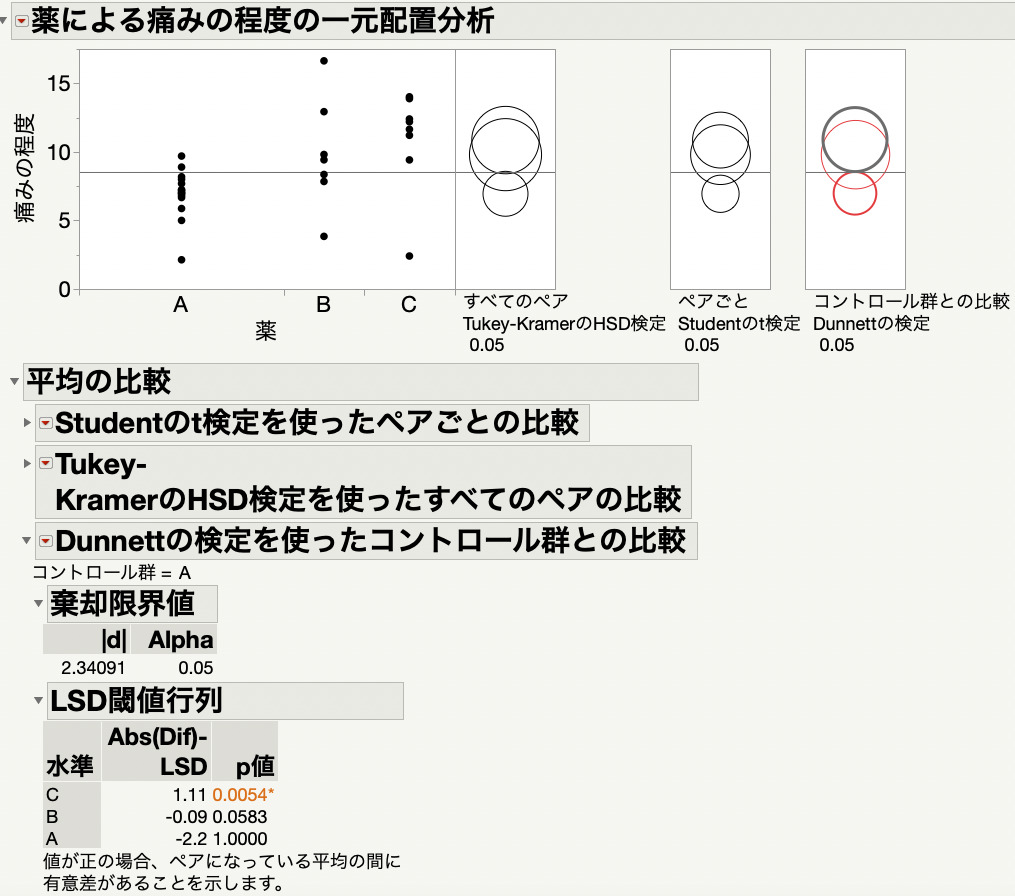
Dunnett検定をJMPで実施する方法は以上です。
Dunnett検定の結果は、Tukey検定の結果とは少し表示のされ方が違います。Dunnett検定で注目していただきたいのは、「LSD閾値行列」の結果です。
3種類のp値が表示されていますが、今回はコントロール群をA群としていますので、水準Aの結果は無視してOKです。(A vs Aの結果には興味がないため)
結果をみると有意水準を0.05とした場合、Tukey検定と同様にA vs Cに有意差があり、A vs Bには有意差がありません。
Dunnett検定を使うことで、多重性を考慮しない全ペアの比較よりも有意になりにくい検定結果が得られていることがわかります。
Tukey検定とDunnett検定の結果の解釈はどうするのか

ここまでで、多重比較検定であるTukey検定とDunnett検定を実施できました。
では、結果の解釈をどうすればいいのでしょうか。
上記で実施した3種類の比較でのP値と検定の数(パラメトリック)を表にまとめてみましょう
| C vs AのP値 | B vs AのP値 | 検定の数 | |
| 多重性を考慮しないt検定 | 0.0027 | 0.0305 | 3 |
| Tukey検定 | 0.0075 | 0.0757 | 3 |
| Dunnett検定 | 0.0054 | 0.0583 | 2 |
Tukey検定もDunnett検定も使用したデータは同じです。
唯一異なるのは「全ペアでの比較」をしたのか「コントロール群に対する比較」だけをしたのか、という違いです。
つまり、検定の数の違いがp値の大小に関わっている、ということが言えます。
多重性を考慮した解析であっても、検定の数が少なくなるような手法を選ぶかどうかで有意になりやすさが変わることがわかります。
まとめ
この記事では、「JMPでパラメトリックな多重比較!Tukey検定とDunnett検定を実施する方法」ということでお伝えしました。
多重性を考慮した検定でも、検定の数が異なればP値も変わってきます。
研究の目的に応じて、どちらの検定が良いかを判断できるようになりましょう!











コメント