データが3群以上ある時の検定でよく用いられるのが分散分析です。
analysis of varianceの頭文字をとってANOVAとか言ったりもします。
同じ分散分析でも、正規分布、非正規分布といったデータの違いによって実施する分析は異なります。
ですので、扱う群のデータが正規分布なのか?非正規分布なのか?を最初の段階で確認する事が重要!
例えば一つの要因の差を分析したい場合、扱う群のデータが正規分布であれば、パラメトリック検定である一元配置分散分析。
非正規分布であれば、ノンパラメトリック検定であるクラスカルウォリス検定。
これらの解析をSPSSではできますので、統計解析ソフトSPSSを使った分散分析の実施方法について具体的に説明していきます。
もちろん、分散分析の結果の解釈についても一緒に見ていきますのでご安心を。
この記事では、一元配置分散分析(パラメトリック検定)と一元配置分散分析のノンパラメトリック検定であるクラスカルウォリス検定について説明していきますね。
SPSSで一元配置分散分析!ANOVAとは?

分散分析は3群以上のデータの母平均の群間に差があるかとうか?を検定する方法。
主に、一元配置分散分析と二元配置分散分析があります。
一元配置分散分析が1つの要因を検討するのに対して、二元配置分散分析は2つの要因を検討する手法になります。
ですので、差を見たい要因が増えるにしたがって三元配置、四元配置となりますが、その分、計算・解釈は複雑になってしまうんです。
SPSSで一元配置分散分析!適用するデータは?
3群以上のデータの母平均の群間に差があるかとうか?を検定したいとき、
3群以上の全ての群のデータが正規分布だった場合、
パラメトリック検定である、一元配置分散分析ができます。
一元配置分散分析は3群以上のいずれかの群間で差があったときに有意確率(p)は有意(p<.05、p<.01、p<.001)となります。
しかし、どの群間で有意差があるのかについては、一元配置分散分析では特定できませんので、多重比較を実施して群間の差を検討するという手順(事後検定)を取ることが多いです。
事後検定には賛否両論ありますので、こちらの記事でご確認ください。
データの条件は以下の通り。
- 検定する各群すべてが正規分布に従うデータであること。(ヒストグラムやQQプロットなどの見た目判断でOK)
- 比率尺度、間隔尺度、また一部例外として段階数の多い順序尺度データ
- 平均を比較することが意味を持つデータ
- 3つ以上の群(標本、変数、サンプル)を対象としたデータ
SPSSで一元配置分散分析(パラメトリック検定)を行う
それでは一元配置分散分析を行っていきましょう。
まずは今回使用するデータを読み込みます。
今回のデータは、各疾患の3群(急性リンパ性白血病、急性骨髄性白血病、骨髄異形成症候群)で生存期間の比較を行います。
- SPSSに直接データを打ち込む場合は、[ファイル]→[新規作成]→[データ]の順に進みます。
- 既にデータ入力が終了している場合は、[ファイル]→[開く]→[データ]で任意のデータを選択します。
- Excelにデータを入力している場合は、[ファイル]→[データのインポート]→[Excel]の順に進み、データをインポートします。
データをセットできたら、そのデータが正規分布であるかどうか検定します(今回は省略)。
各群のデータすべてが正規分布だった場合に限り、一元配置分散分析を行えます。<!–
その後[分析]→[平均の比較]→[一元配置分散分析]を選択するとウィンドウが表示されます。
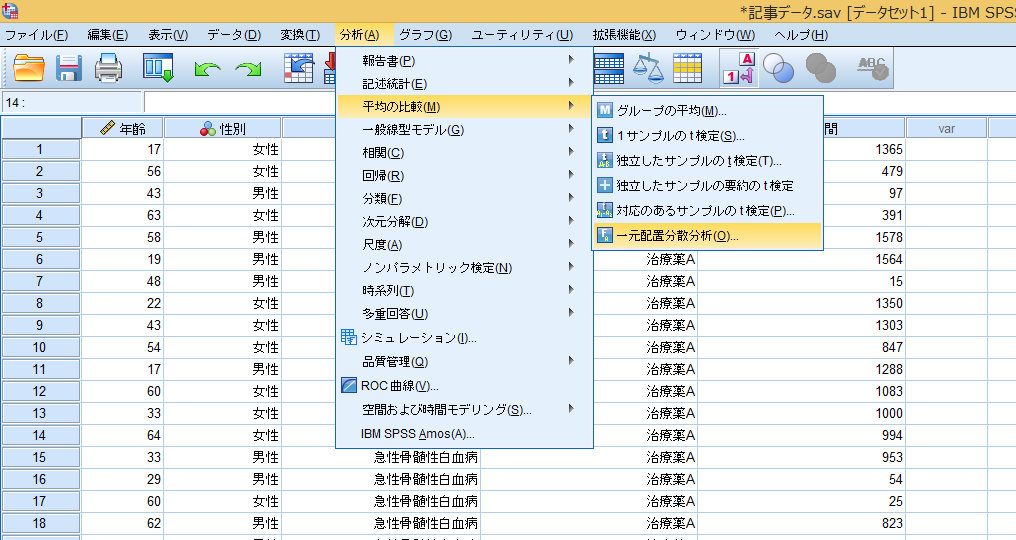
各群の名義尺度データを[因子]のボックスに、平均値の比較をしたい変数を[従属変数リスト]のボックスに矢印➡か、ドラッグ&ドロップで入力してください。
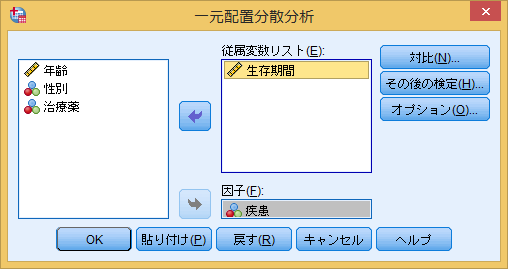
通常、一元配置分散分析の後にどの群間に差があるかを検討する目的で多重比較を実施しますが、その際は[その後の検定]を選択し、任意の検定法を✓します(今回は省略します)。
オプションでは[記述統計量]、[等分散性の検定]、[Welch]に✓します。
SPSSで出力した一元配置分散分析の結果の見方
下記のように、分散分析表が出力されています。
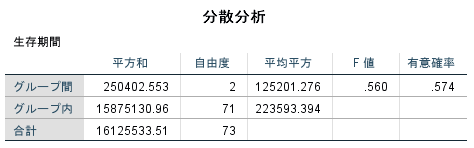
「有意確率」とある部分が、P値を示しています。
今回は0.574のため、P値は有意水準の0.05より大きいため、有意差がない、ということです。
SPSSでクラスカルウォリス検定
次に、ノンパラメトリック検定であるクラスカルウォリス検定をSPSSで実施する方法をご紹介します。
SPSSで実施できるクラスカルウォリス検定とは?適用条件となるデータ
3群以上のデータの母平均の群間に差があるかとうか?を検定したいとき、
3群以上のいずれかの群のデータが一つでも非正規分布だった場合、
パラメトリック検定である、一元配置分散分析はできません。
その時はノンパラメトリック検定であるクラスカルウォリス検定をしてください。
クラスカルウォリス検定は一元配置分散分析と同様、3群以上のいずれかの群間で差があったときに有意確率(p)は有意(p<.05、p<.01、p<.001)となります。
しかし、どの群間で有意差があるかについては、クラスカルウォリス検定だけでは特定できませんので、多重比較を実施して群間の差を検討します。
SPSSでクラスカルウォリス検定後の多重比較はできません。
データは以下に従っている必要があります。
- (1)正規分布以外に従うデータであること。
- (2)比率尺度、間隔尺度、または順序尺度データ
- (3)中央値を比較することが意味を持つデータ
- (4)3つ以上の標本を対象としたデータ
SPSSでクラスカルウォリス検定を行う
それではクラスカルウォリス検定を行っていきます。
まずは今回使用するデータを読み込みます。今回のデータは、一元配置分散分で用いた同じデータを用います。
データがセットできたら、そのデータが正規分布であるかどうか検定します(今回は省略)。
各群のデータが正規分布ではなかった場合に、クラスカルウォリス検定を行います。
その後[分析]→[ノンパラメトリック検定]→[過去のダイアログ] →[K個の独立サンプルの検定]を選択するとウィンドウが表示されます。
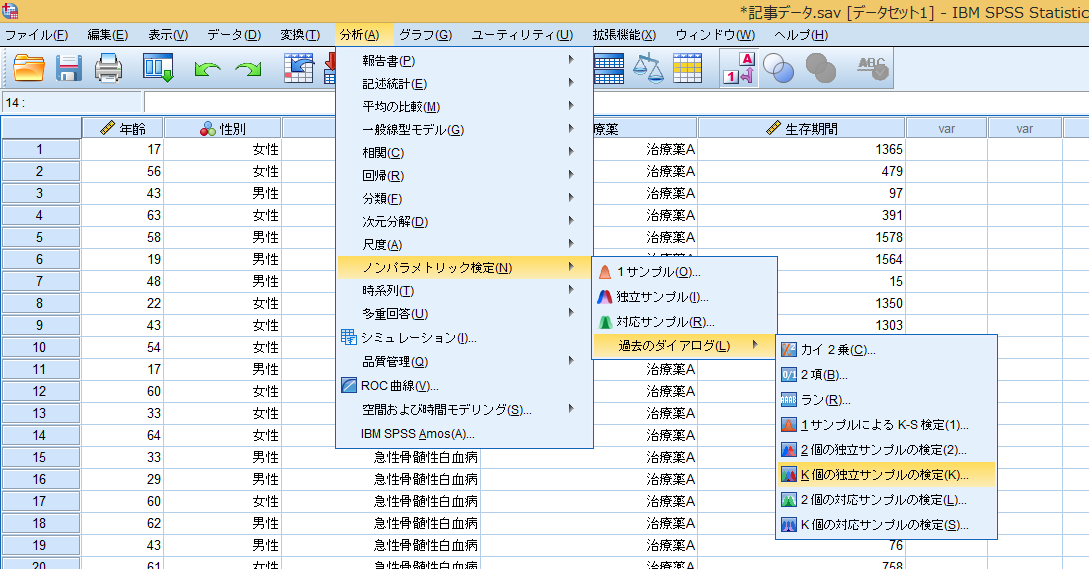
各群の名義尺度データを[グループ化変数]のボックスに、中央値の比較をしたい変数を[検定変数リスト]のボックスに矢印➡か、ドラッグ&ドロップで入力します。そして[検定の種類]で[Kruskal-WallisのH]に✓をします。
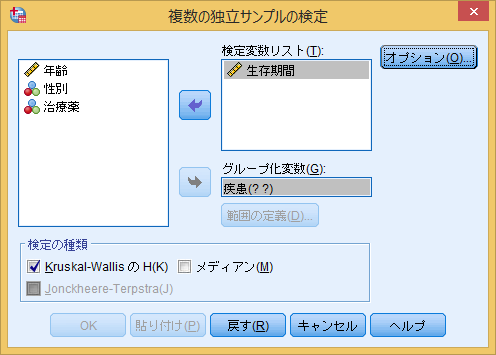
[グループ化変数]の[範囲の定義]を選択し変数の範囲を入力します(今回は最小1、最大3と入力します)。そして[続行]を選択し分析を行います。
※分析の結果、漸近有意確率はp=0.533なので有意差はありませんでした。

SPSSで分散分析(ANOVA)まとめ
今回は一元配置分散分析とクラスカルウォリス分析を実施しました。
何度も言いますが、初めに各群のデータが正規分布かどうかを確認し、各群すべてのデータが正規分布であれば一元配置分散分析を、そうでなければクラスカルウォリス分析を実施します。
二つの分析とも基本的な考え方は同じです。
実際に分析して理解を深めましょう。











コメント