日本製薬工業協会から発出された「医療用医薬品情報概要等に関する作成要領」が2023年10月に改定されました。
その中で特に着目すべきことは「検証的な解析によるp値」と「名目上のp値」を明確に分けて記載するように求められていること。
統計の専門家でなければ、p値が検証的かどうかに分かれるということはイメージしにくく、同じp値であっても全く意味が異なる数値であると言われても、それを理解することは難しいですよね。。。
そのため今回は、なぜ「検証的な解析によるp値」と「名目上のp値」を分ける必要があるのかをわかりやすく解説します!
名目上のp値とは?p値は3種類に分けられる
もしかしたらあまり意識したことはないかもしれませんが、臨床試験で得られるp値は3種類に分けることができます。(医療用医薬品情報概要等に関する作成要領p51参照)
- 検証的なp値…事前に検出力(1-βエラー)を制御してサンプルサイズが決められており、αエラーに対する多重性への対処がなされている
- 検証的ではないが多重性を制御したp値…事前にサンプルサイズは決められていないが、αエラーに対する多重性への対処がされている
- 名目上のp値…事前にサンプルサイズは決められておらず、αエラーに対する多重性への対処もされていない
まり、αエラー(第一種の過誤)とβエラー(第二種の過誤)を適切に制御しているかどうかによって、得られるp値の信頼度合いも変わってくるということ。
復習にはなりますが、αエラーとβエラーはそれぞれ以下の意味を持ちます。
- αエラー:本当は差がない(もし仮に母集団を全て調べることができたら真実は差がない)のに、今回のデータ(標本データ)でたまたま統計的に有意であると判断してしまうエラー
- βエラー:本当は差がある(もし仮に母集団を全て調べることができたら真実は差がある)のに、今回のデータ(標本データ)でたまたま統計的に有意ではないと判断してしまうエラー

臨床試験における統計的検定の目標はαエラーとβエラーを制御することであり、適切なサンプルサイズ設計がなされてあることが前提で成り立っています。
そのため、αエラーとβエラーを完全に無視したp値は、全くもって主張や意思決定の根拠になり得ないのです。
名目上のp値の「名目」ってどんな意味?
αエラーとβエラーを適切に制御しているか否かで、p値は3種類に分けられることがわかりました。
ではここで、そもそも「名目上」とはどんな意味があるかを確認しましょう。
weblio辞典で「名目」を検索してみると「表向きの名称」という意味があるようです。
そのため「名目上のp値」を直訳すれば「表向きのp値」ということになります。
これはつまり、αエラーもβエラーも適切に制御することなく、得られたデータから単に計算されただけのp値、という意味です。
では「名目」の対義語をweblio辞典で検索してみると「実質」であることがわかります。
そして「実質」をweblio辞書で調べてみると「実質(じっしつ)とは、事物の本来の内容や性質を指す言葉である。形式や外見だけでなく、そのものが持つ根本的な特徴や機能を意味する。」とあります。
つまり、実質的なp値とは、p値が有意水準を下回ったか否かによって意味を持つようなp値。
すなわち、αエラーとβエラーを適切に制御された検証的なp値のことを指します。
ではここまでの解説をもとにして、2023年10月に改定された「医療用医薬品情報概要等に関する作成要領」の「検証的な解析によるp値」と「名目上のp値」の記載を確認してみます。(医療用医薬品情報概要等に関する作成要領p51参照)
- 検証的な解析によるp値
- 試験の主要な目的や試験デザインに直結する仮説について、第1種の過誤、検出力を考慮して例数設計された試験における検証的な解析結果は、どのような結果が得られれば、医学的に意味があり、統計学的にも支持されるのかが十分に事前検討された解析結果です。
- 検証的な解析結果は、試験の成否や、規制当局による承認等の意思決定の判断等に用いられることがあります。
- 名目上のp値
- 検証的な解析以外の解析で得られた p 値は、「名目上の p 値」と呼ばれます。
- 「名目上の p 値」、単に統計的な仮説検定の手順に従って計算された p 値であり、その値が典型的な有意水準である 5%(0.05)より小さくても、結果の重要性や、証拠の強さを示すものではありません。
したがって、「名目上の p 値」は、その値を主張や意思決定の拠り所にはできないという意味において“解釈できない p 値”なんです。
なぜ事前にサンプルサイズ計算をしていないと名目上のp値か検証的なp値かが変わるのか?
前章までを見ると「αエラーとβエラーを適切に制御しているか否か」によって、p値の信頼性が変わることがわかりました。
ではなぜ、「事前に検出力(1-βエラー)を制御し、サンプルサイズも決められている」ことが重要なのでしょうか。
結論から言えば、「p値はサンプルサイズに依存する」からです。
そのことを理解していただくために、架空のデータでサンプルサイズがp値に影響を与えていることを確認しましょう。
A群は平均0の標準偏差2の正規分布に従うデータ、B群は平均1の標準偏差2の正規分布に従うデータを、エクセルで乱数を発生させてみました。
そして各群10例の場合のt検定の結果、各群30例の場合のt検定の結果を示したのが下記の表です。

上記の表を見ると分かる通り、平均値の群間差はn=10の場合でもn=30の場合でも、ほとんど変わりません。
しかし、p値を見るとn=10の場合は0.185であり、n=30の場合は0.024です。
仮に有意水準が0.05であった場合、n=10の結果は有意差なし、n=30の結果は有意差ありという結論になります。
このように、平均値の群間差が同じで合ったとしても、サンプルサイズが大きいことによってp値が小さくなるのです。
サンプルサイズを大きくすれば誰でも有意差が出せてしまう
この結果を見ると、一つのことがわかります。
それは「サンプルサイズを大きくすれば、どんなデータでも有意差が付く可能性がある」ということ。
例えば、収縮期血圧の平均値の群間差が1mmHgの差だったとしても、サンプルサイズが十分に大きければ有意差が出せてしまうのです。
でも、考えてみてください。収縮期血圧の1mmHgの差は、臨床的にどれだけ意味のある差でしょうか?
同じ人でも血圧を2回測定したら、それだけで1mmHgの違いなんて簡単に出てきます。
全くと言っていいほど、臨床的に意味はない差ですよね。
そのため私たちが気にしなければいけないことは、臨床的に意味のある差を統計学的に検出できているのか?という視点です。
この視点がない限り、得られたp値は単なる数値のお遊びでしかなくなります。
そのため、「臨床的に意味をもつ最小限度の効果又は新しい試験治療の予想される効果」を事前に明記し、その効果に対して適切にサンプルサイズ計算をしなければ、得られているp値が単にサンプルサイズの大きさによって左右されているだけかどうかが分かりません。
だからこそ、検証的なp値の要件に「検出力(1-βエラー)を考慮して例数設計されたかどうか」が必要なのです。
なぜ多重性を考慮していないと名目上のp値になるのか?
次にここでは「第1種の過誤(αエラー)を適切に制御する」重要性をお伝えします。
第1種の過誤(αエラー)が問題になるのは、一つの試験で統計的仮説検定を2回以上実施する場合に発生する場合です。
いわゆる「多重性の問題」として知られています。
多重性の問題を考える上で重要なのがファミリーワイズエラー率(Family-wise Error Rate: FWER)という概念。
FWERとは、一つの試験の中で複数の検定を実施したときに「どれか一つでも有意になる確率」のことであり、FWERを考慮することは、端的に言えば「個々の検定ではなく、試験全体としてのαエラーを適切に制御しましょう」ということです。
仮に試験全体で検定が1つであれば、1つの検定=試験全体のαエラー、とみなせますので、特にFWERを考える必要がありません。
しかし検定が2つになってしまうと、「2つの検定のうちどちらか一つでも有意になる確率」は「1-どちらも有意にならない確率」となりますので、1-(0.95)2=9.75%になってしまうのです。
3つ以上の検定を実施した場合、いずれかの検定が1つでも有意になる確率は、どんどん上昇します。つまり、試験全体としてのαエラーが0.05よりも大きくなってしまうということなのです。
1つの検定だけで有意かどうかを判断する状況よりも、3つの検定のうちどれか1つでも有意になればいい状況の方が、試験実施者に有利なことは言うまでもありません。
つまりαエラーを制御するということは「数うちゃ当たる」や「複数の結果のうちいいとこ取りをする」という問題をなくした状況を作らなければならない、ということです。
αエラーとβエラーを事前に制御しているかでp値は3種類に分けられる
ここまでの話をまとめると、事前にサンプルサイズ計算をしているか否か、そして、αエラーが制御されているか否かによって、「医療用医薬品情報概要等に関する作成要領」のp51に記載されているような3種類のp値に分けられます。
(ゲートキーピング法でαエラーを制御している場合)
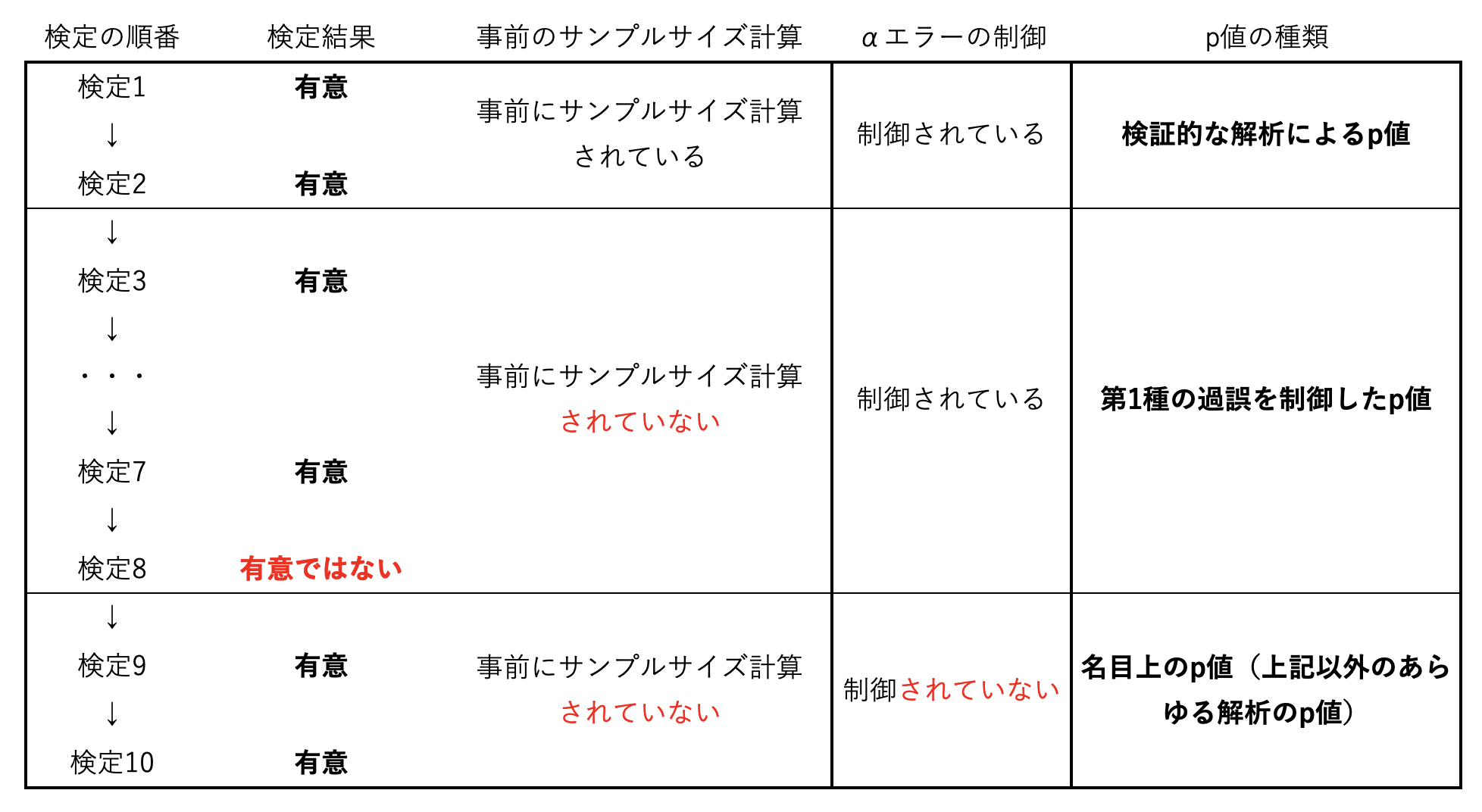
注意すべき点は、名目上のp値は「検証的な解析によるp値」と「第1種の過誤を制御したp値」以外の、あらゆる解析のp値であるということです。
例えば、サブグループ解析などでp値を出力したとしても、そのp値は名目上のp値になります。
なぜなら、サブグループ解析は事前にサンプルサイズ計算がされているわけではありませんし、αエラーも制御されていないからです。
名目上のp値は意味がないのか?
ここまで解説すると、もしかしたら「名目上のp値は意味がないのか?」と疑問に思われる方もいるかもしれません。
しかし勘違いしていただきたくないのは、名目上のp値は「それ単独で解釈できないp値(つまり、0.05を下回ったかどうかで判断できないp値)」ということであり、名目上のp値に対しては他の情報で補強することによって解釈をすることが、科学的に適切なアプローチになります。
ASA声明の原則3にある通り、「科学的推論を行う際、研究者はさまざまな背景情報を利用すべきであり、それには研究のデザイン、測定の質、研究対象である事象のこれまでのエビデンス、データ解析の背後にある仮定の妥当性が含まれている。「可否」による二分類の決定は実用的ではあるが、P値だけで決定が正しいかどうかが保証されるものではない。」ということです。
つまり、その研究に至るまでのありとあらゆる結果(先行研究など)があるはずであり、それら結果との整合性がどうなっているのかを科学的に解釈することが重要なのです。
まとめ
この記事ではなぜ「検証的な解析によるp値」と「名目上のp値」を分ける必要があるのかを解説いたしました。
p値を解釈する上で、αエラーとβエラーを適切に制御しているか否かがとても重要になります。
ぜひ、同じp値であっても、事前に計画を練られているかどうかによって信頼性が全く異なることを理解していただければ幸いです!














コメント