統計学では、確率密度や確率密度関数といった語句がよく出てきます。
これらの言葉は、”確率”としばしば混同されて使われていますが、確率と確率密度は大きく異なります。
では、確率と、確率密度や確率密度関数は何が違うのでしょうか。
この記事では、統計学での重要単語”確率密度と確率密度関数”についてわかりやすく出てきます。
確率密度関数とは?理解するのに重要な確率変数

確率密度の話をするには、はじめに確率変数の話をする必要があります。
確率変数は、”ある変数の値をとる確率が存在する変数”です。
例えば、サイコロを例にして考えてみましょう。
サイコロは1、2、3、4、5、6と6つの目があります。
サイコロの各目が出る確率は1/6ですから、それぞれのサイコロの目は確率変数です。
身長の例を考えてみましょう。
身長のデータが得られて、ヒストグラムを作成してみると、下記のようになります。
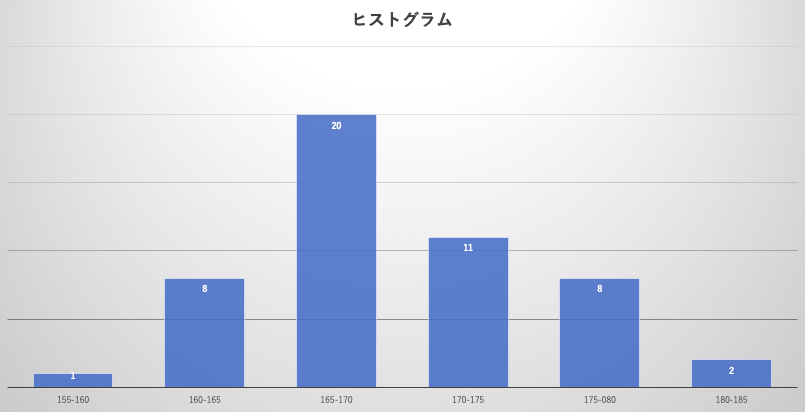
そして、上記のヒストグラムを滑らかにしてみると、下記のようなグラフになります。

確率変数は、上の2つ図では横軸にあたります。
この確率変数は、確率変数の性質によって、
- 離散確率変数
- 連続確率変数
2種類に分けることができます。
離散変数は上のヒストグラムやサイコロの目のように、変数が飛び飛びで存在しているものを指します。
>>>ヒストグラムとは?エクセルでの作成方法と解釈を簡単にわかりやすく
サイコロの目は1から6と連続のように思えますが、これは飛び飛び、つまり離散的です。
連続な値は1、1.0000001、1.001111といったように、シームレスに繋がった値のことです。
1、1.1、1.2のような小数刻みでも離散的な値になります。
確率変数が離散的な場合、各変数が生じる可能性が”確率”
離散的な変数の時とき、各変数が生じる可能性を”確率”と言います。
これは中学や高校などでも習う概念で、サイコロの目や、コインの表と裏のような話です。
ここではサイコロを例に考えてみます。
サイコロで1が出る確率は1/6です。
つまり各目が出る確率は1/6で、確率変数が6個あるので、
サイコロを振ってどれかの目が出る確率は1/6 x 6 = 1となります。
確率変数が連続変数の場合は?
次に、連続確率変数を考えます。
連続確率変数は上の2つ目の図のように、変数が連続的なものを指します。
例えば、1から6までの連続確率変数があったときに生じうる変数は、1.1や1.1111、1.010101といった様々な変数をとることができます。
もし、サイコロの時のように1から6までの値が生じる可能性が1/6の一様だったとしましょう。
このとき、どれかの値が出る可能性はどうなるでしょうか。
離散変数と同じように、確率で考えた場合。
1/6 X 無限 = 無限
と可能性が1ではなくなってしまいます。
これはおかしいですよね。
つまり、連続変数の場合では、従来の確率の概念を使うことができなくなってしまいます。
確率密度とは?一様分布の例で面積との関係や求め方をわかりやすく!

先ほど、連続確率変数では、確率の概念を用いるとおかしくなるということを見ました。
そこで、用いる概念を確率密度と呼びます。
先ほどの例を考えますと、1から6までの連続確率変数で、全ての値が一様な可能性で出るとします。
このような時は、1から6までの値の合計、つまり、何かの値が出る確率が1になるように定義します。
イメージは下の図ですね。
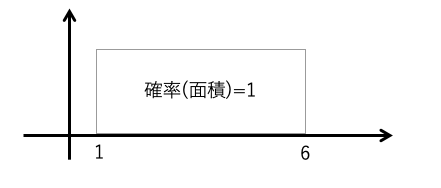
このイメージで高さに対応するものが、確率密度になります。
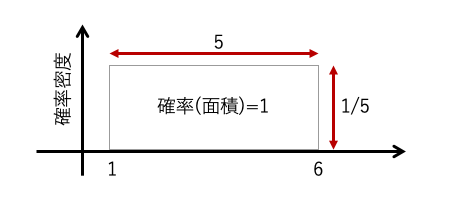
横の幅は6 − 1 = 5で、5ですので、確率密度は1/5となります。
では、ここで問題です。
上の例で2が出る”確率”はいくらでしょうか。
答えはほぼゼロです。
理由は、1/無限 = ほぼゼロだからです。
では2ぐらいの値(1.5から2.5まで)が出る確率はいくらでしょうか?
答えは1/5です。
この理由は、1/5x (2.5 −1.5) = 1/5 だからです。
連続変数では、高さが確率密度で面積が確率
このように、連続変数では確率は面積に対応します。
確率密度は上記の図で言うと、面積の高さに相当します。
高さである確率密度に、横幅である確率変数の範囲をかけて面積を求めることでようやく確率になります。
確率変数の幅というのは、以前に正規分布のところで出てきました。
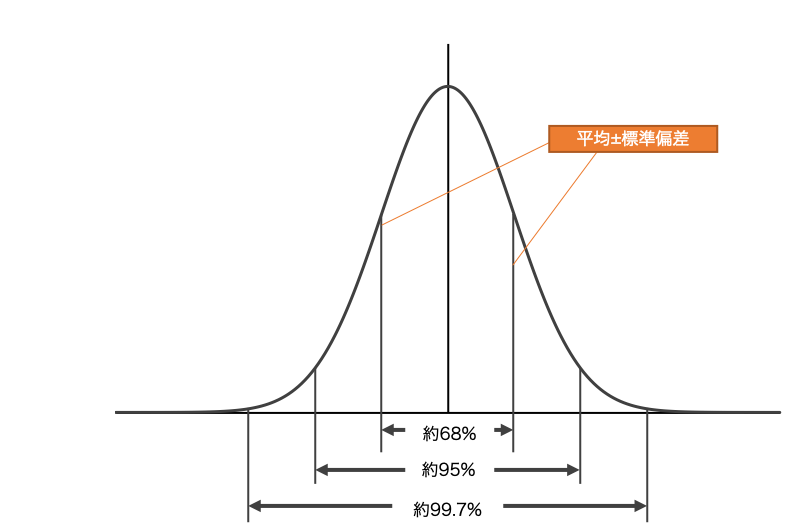
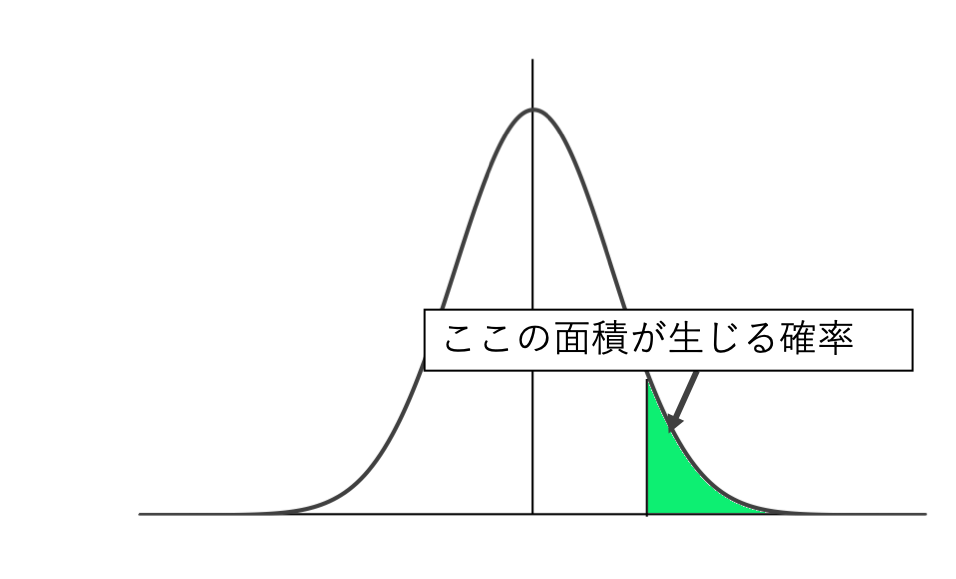
これですね。
ある範囲に値が含まれている可能性という考え方は、統計学では広く用いられており、
それに伴い、確率密度の概念も広く用いられています。
>>>正規分布とは?簡単にわかりやすく標準偏差との関係やエクセルでのグラフ化を解説
>>>標準正規分布表の見方について!標準化やZ値の計算式はどうすればいい?
確率密度関数とは?正規分布の場合を例にわかりやすく
確率密度関数は確率密度と確率変数の関係を表した関数のことを表しています。
代表的な確率密度関数といえば、
正規分布の関数がそれにあたります。

これですね。
>>>正規分布とは?簡単にわかりやすく標準偏差との関係やエクセルでのグラフ化を解説
ここでは、難しい数式は取り上げませんが、確率と確率密度の関係は一般的には積分の形で表しています。
確率密度関数に関するまとめ

離散確率変数では、ある確率変数が生じる可能性を確率という
連続確率変数では、確率密度という概念を用いる。
連続確率変数では、確率密度と確率変数の幅の積が、確率に相当する。
連続確率変数と確率密度の関係を表したものを確率密度関数という。
確率密度は少し難しい概念ですが、統計学で非常に重要な概念です。
少しずつ慣れていきましょう!!













コメント
コメント一覧 (1件)
[…] […]