この記事では条件付き確率について学んでいきます。
条件付き確率は、統計検定2級でも頻出するのでぜひ理解しましょう。
この記事を見れば、これらのことがわかります。
- 条件付き確率とは?その公式は?
- ベン図で見る、条件付き確率
- 条件付き確率を、サイコロのわかりやすい例で理解
- ベイズの定理との関係
では早速学んでいきましょう!
ちなみに、2018年11月に実施された統計検定2級の問題でも、条件付き確率が出てきています。
条件付き確率とは?公式や記号の読み方を確認する

そもそも、どんな問題が与えられたときに「条件付き確率を求めればいいんだな!」となるでしょうか。
条件付き確率を考える前に、普通の確率計算について考えてみましょう。
通常の確率計算ではこのような問題文が与えられたときに求めれば良いですよね。
これが間違いなく、普通に確率を求める問題です。
では条件付き確率を求めなければいけない問題はどのような問題でしょうか。
これが、条件付き確率を計算しなければならないときの問題です。
つまり「〜が起こったときに」とか「〜が起こった条件のもとで」という言葉があったら、条件付き確率を計算すればいいんだな、ということです。
条件付き確率の定義(公式)
それが分かったところで、条件付き確率の定義(公式)です。
全部理解する必要はないので、こんな数式なんだー、ぐらいに思ってもらえれば今のところは大丈夫です。
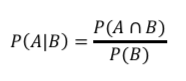
ここで、P(A)やP(B)というのは、「Aが起こる確率」や「Bが起こる確率」のことです。
P(A|B)というのが、「Bが起こった条件のときのAの確率」のことです。
この条件付き確率の数式の書き方は暗記するしかありません。
条件付き確率の読み方
ちなみに、このP(A|B)の読み方に関しても、疑問に思われれる方が多いです。
読み方に正解はないのですが、日本語だったら「Bが起こったときにAが起こる条件付き確率」と読めばいいかと思います。
英語では、「Probability of A given B」ですかね。
英語の方がシンプルですね。
直訳すると「Bが与えられた時のAの確率」。
まさに、条件付き確率です。
そして分子にあるこの数式。
![]()
これは「AかつBが起こる確率」のことです。
つまり、AとBが同時に起こる確率、ということです。
これらを踏まえて。
条件付き確率を日本語で書くと以下のとおりになります。
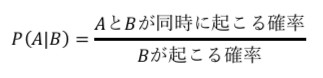
これが、条件付き確率の定義です。
条件付き確率はベン図で見るとわかりやすい

定義だけだとよくわからない気がするので、図を使ってイメージで覚えましょう。
確率を図式化するのに有効なのが、ベン図です
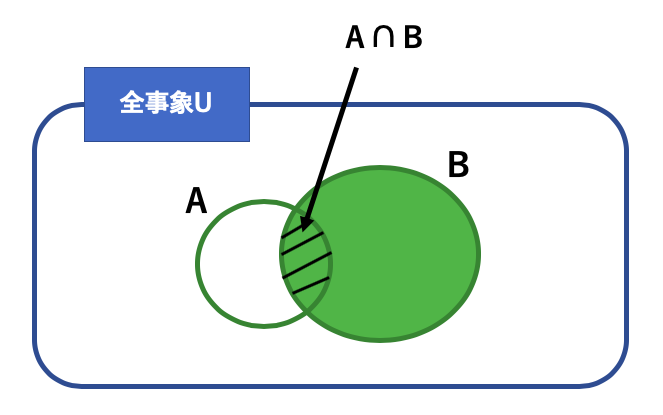
この図を見ると分かりやすいですね。
つまり条件付き確率というのは、緑色の面積(Bの確率)のうち斜線で引いた部分の面積(AとBが同時に起こる確率)がどれくらいあるかということを、求めるものです。
では、以下のようなベン図だったらどうなるでしょうか?
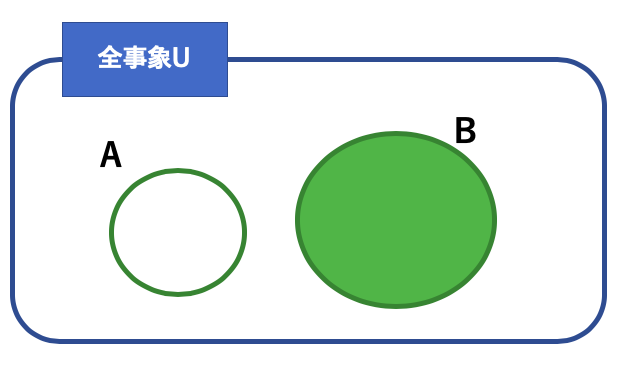
重なっている部分がないですよね。
この時は、AかつBが0になります。
よって、条件付き確率も0になります。
条件付き確率をサイコロの例で学ぶ

それでは、例題を解きながら条件付き確率を深く理解しましょう。
数式で書くとP(3以下|奇数)ですね。
では、どういう式で求めることができるでしょうか。
条件付き確率の定義は以下の通りでした。
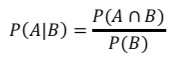
ということは、今回の問題ではこのように数式を書くことができますよね。
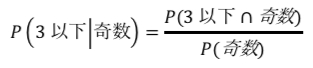
P(奇数)=1/2であり、P(3以下かつ奇数)=2/6=1/3です。
よって、P(3以下|奇数)=2/3となります。
ベン図で書くと、以下の通り。
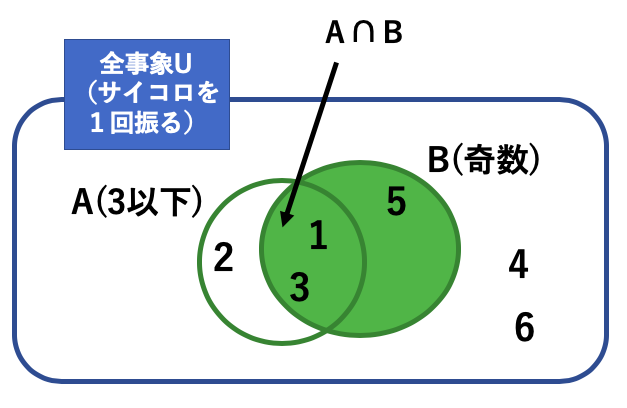
今回の問題の全事象Uは、「サイコロを1回振る」ってことですよね。
そして、Aが3以下の目が出る。
Bが奇数の目が出る。
で、AでもBでもないのが4と6です。
ベン図で書くと、かなりわかりやすいですね。
条件付き確率とベイズの定理の関係
条件付き確率は、ベイズの定理とかなり密接な関係があります。
ここから先は少し発展した内容になりますので、条件付き確率は完璧!でありベイズの定理も知っておきたい!という方のみご覧くださいね。
まず、ベイズの定理はこのような式です。
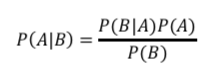
この式が何を意味しているのかというと、このような感じです。
これが、ベイズの定理がやっていること。
ちなみに、なぜこのような式になるか。
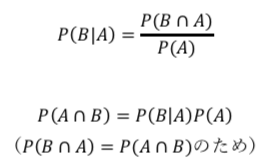
なので、これで得られた式を条件付き確率に代入すると、ベイズの定理が導かれる。
ベイズの定理がどんなところで使われているのか?については、また別の記事で。
条件付き確率に関するまとめ

- 条件付き確率とは「〜が起こった時に、〜が起こる確率」のこと。
- ベン図を使ってイメージで覚えると、覚えやすい。
- ベイズの定理との関係があるため、ベイズの定理を理解する第一歩は条件付き確率を理解すること。











コメント