今回の記事では、2017年11月に実施された統計検定2級の過去問を解説します。
問題を無断で貼り付けることができないため、実際の問題については、問題集をご購入ください。
2018年11月に実施された統計検定2級の過去問の解説もしています。
2018年6月に実施された統計検定2級の過去問の解説もしています。
統計検定2級の過去問解説(2017年11月):問1(1)
この問題で重要なことはただ一つ。
ということ。
これさえわかればOKです。
100-(0.93+5.25+35.80+38.27+5.25+0.62) = 13.88%
統計検定2級の過去問解説(2017年11月):問1(2)
1: ×
滞在日数が1週間未満であるということは、(A)と(B)の階級を足した割合のことである。最も高いのは韓国である。
2: ×
もっとも割合が高い階級は(C)である。
3: ×
(C)の階級で50%以上の割合がいる。
4: ×
(A)と(B)を加えると、90%を超える。
5: ◯
累積度数(上から足した度数)が50%を超える階級がフランスでは(D)であり、その他の国は(B)か(C)である。そのため、中央値がもっとも大きい国はフランスである。
統計検定2級の過去問解説(2017年11月):問1(3)
縦軸に注目する。
米国では、(C)の階級が50%を超えているため、1か2のグラフのいずれかであることがわかる。
また、(C)の両隣である(B)と(D)が19%と18%という、ほぼ同じ割合であることから、1が該当する。
統計検定2級の過去問解説(2017年11月):問2(1)
相関係数と散布図のグラフの対応を読み取れるかどうかが 鍵になる。
まず、開花日と平均気温は相関係数が-0.789である。
強い負の相関が見られることから、Iが平均気温の散布図であることがわかる。
降水量の合計の相関係数は正であり、日照時間の合計の相関係数が負であることから、IIが降水量の合計、IIIが日照時間の合計であることが読み取れる。
統計検定2級の過去問解説(2017年11月):問2(2)
t値は、回帰分析の係数を標準誤差で割ったものである。
そのため、標準誤差をsとすると、以下の数式で解くことができる。
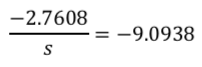
よって、s=0.3036となる。
統計検定2級の過去問解説(2017年11月):問2(3)
回帰係数の表と問題文から、以下の数式をイメージできたかどうかが鍵になる。
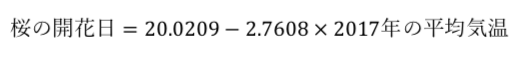
この数式を解くと、開花日は3.17となり四捨五入して3日である。
3月31日が0であるから、3日は4月3日となる。
統計検定2級の過去問解説(2017年11月):問3(1)
中央値を求めるためには、データを小さい順に並べ替える必要がある。
キャベツのデータを並べ替えると、以下のようになる。
| 149 | 154 | 174 | 180 | 183 | 213 | 215 | 218 | 230 | 242 | 256 | 356 |
この時の真ん中の値が中央値になる。
データの数が偶数であるため、中央値は真ん中2つのデータの平均値である。
よって、(213+215)/2=214となる。
変動係数は、標準偏差/平均値であるから、56/214.2=0.261となる。
統計検定2級の過去問解説(2017年11月):問3(2)
箱ひげ図より、キャベツのデータは大きい方に外れ値が2つある。
また、ビールのデータは、大きい方に外れ値が1つある。
そのため、キャベツのヒストグラムはIIIであり、ビールのヒストグラムはIIであることがわかる。
統計検定2級の過去問解説(2017年11月):問3(3)
この問題で重要なのが、コレログラムの読み取り方。
ある時点のデータAと、そこから時点をずらしたデータB(ラグ)があったとき、AとBの数値を用いて、自己相関係数を算出することができます。
コレログラムとは、横軸にラグを時系列的に示し、縦軸に自己相関係数を示したもの。
コレログラムを使えば、データに周期性(例えば季節変動など)があるかどうかを調べることができます。
I:◯
コレログラムから、キャベツの価格における1年後(12ヶ月後)との相関は5%棄却限界値より大きく、ビールの価格における1年毎の相関は5%棄却限界値より小さい。
II:◯
コレログラムから、ラグ1の自己相関係数が0.5あり、5%棄却限界値より大きい。
ラグ1の自己相関係数は各月の価格とその翌月の価格の相関係数を表す。
したがって、ある月の価格が平均より高ければ、その翌月の価格も平均より高い傾向があることがわかる。
III:×
コレログラムは、1つの時系列の時間的相関を表すグラフである。
したがって、2つの時系列間の時間的な相関を見ることはできない。
よって、キャベツとビールの価格の時間的相関関係を読み取ることはできない。
統計検定2級の過去問解説(2017年11月):問4(1)
ラスパイレス指数の計算式を知っていれば解ける問題です。

つまり、今回の問題だとこのような式になります。
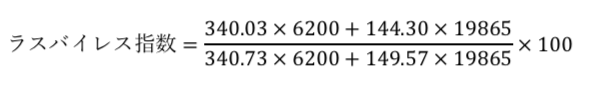
統計検定2級の過去問解説(2017年11月):問4(2)
価格指数のグラフを見ると、1970年〜1980年には10%を超えるプラスの変化がある。
そのため、1か3が該当する。
また、1990年以降は、マイナスの変化もあることから、全てプラスの変化率である1は間違いである。
よって、3が該当する。
統計検定2級の過去問解説(2017年11月):問5
抽出に関する基本問題です。
I:◯
これは正しいです。
II:×
多段抽出法は、コストは削減できるが偏りが生じやすい抽出法です。
例えば全国の世帯調査の際に、1段目に都道府県を抽出し、2段目に市町村を抽出する、というやり方が多段抽出法の例です。
1つの市町村だけを調査するためコストが削減できますが、その市町村が全国の世帯の代表データになるため、偏りが生じている可能性があります。
III:◯
これは正しいです。
統計検定2級の過去問解説(2017年11月):問6
実験研究と観察研究の違いは、実験者が介入するものを決めている場合が実験研究で、 被験者自らが介入を選び実験者はそれを観察するだけという場合が観察研究である。
1: 実験研究
新薬か対照薬かは、実験者がランダムに割り当てている。
2: 実験研究
アサガオの育成条件を、実験者が決めている
3: 観察研究
健康食品を食べるかどうかは、参加者が決めている。
4: 実験研究
どちらの部屋に入るか、実験者が決めている。
5: 実験研究
スピードの条件は、実験者が決めている。
統計検定2級の過去問解説(2017年11月):問7
問題を解く上で必要な知識は、条件付き確率である。
問われているのは、おもちゃが不良品だった場合に、工場Aで生産されていた確率であるから、数式にすると以下の通り。
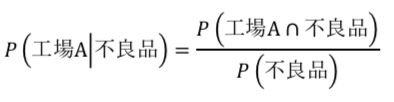
おもちゃが工場Aで作られ不良品である確率は0.6*0.01である。
また、おもちゃが工場Bで作られ不良品である確率は0.4*0.005である。
よって、P(不良品)は0.6*0.01+0.4*0.005である。
P(工場A∩不良品)は0.6*0.01である。
よって、以下の計算式になる。

統計検定2級の過去問解説(2017年11月):問8(1)
確率の定義の一つに「全て足すと1になる」という性質があります。
確率密度関数f(x)が与えられた時、積分をすると確率密度関数の面積が求まります。
その面積が「全て足すと」に該当するため、今回の問題では以下の数式を満たします。
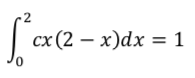
これを計算していけば良いです。
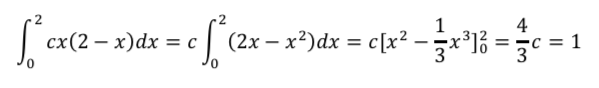
統計検定2級の過去問解説(2017年11月):問8(2)
平均値と分散の定義通りに計算する問題です。
以下の数式は暗記しておきましょう。
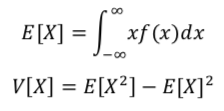
与えられたf(x)を使って、まずは平均値を求めます。
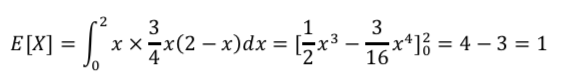
次に、分散です。
その前にE[X2]を計算しておきます。
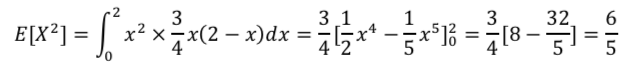
よって、分散は以下の式になります。
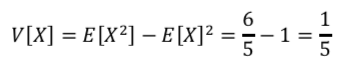
統計検定2級の過去問解説(2017年11月):問9(1)
問題文の各式は、(ア)カイ二乗分布、(イ)t分布、(ウ)F分布の式である。
統計検定2級の過去問解説(2017年11月):問9(2)
YがF分布の定義に従っていることに気づきましょう。
その上で、Yは自由度(20, 10)のF分布に従っています。
しかし、F分布表では「上側パーセント点」しか与えられていませんが、問題文はY≦αより、「下側パーセント点」を求められています。
そのため計算を工夫し、1/Yが自由度(10, 20)のF分布に従うことを利用します。
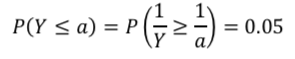
F分布表より、1/a=2.348となるため、a=1/2.348です。
統計検定2級の過去問解説(2017年11月):問10(1)
まず必ず知っておきたいのが、正規分布の性質。
正規分布は「平均値(μ)」と「標準偏差(SD)」の2つで形が決まります。
そして、μ±SDの間には、約68%のデータが含まれています。
μ±2SDの間には、約95%のデータが含まれています。

今回は、60点以上の確率であるため、以下の式を満たします。
(1-0.68)/2=0.16
統計検定2級の過去問解説(2017年11月):問10(2)
60点以上取る確率は0.16であり、60点未満を取る確率は0.84であるため、5人中1人が60点以上取る確率は以下の通り。
![]()
統計検定2級の過去問解説(2017年11月):問10(3)
Y=(X1+…+X5)/5とした時、Yは平均値50、標準偏差10/√5に従う。
ちなみに、SD/√nは標準誤差とも呼ばれる。
よって、標準正規分布に従う確率変数をZとするとき、以下の数式で計算することができる。
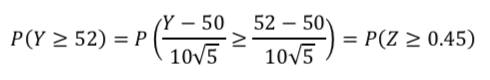
標準正規分布表より、0.45となる点は0.173であるから、0.5-0.173=0.327となる。
統計検定2級の過去問解説(2017年11月):問11(1)
パラメータがλのとき、ポアソン分布の平均値はλ、分散もλである。
よって問題文から、分散の推定値は518/365である。
統計検定2級の過去問解説(2017年11月):問11(2)
1日に事故が発生しない確率は、P(X=0)を計算すれば良い。
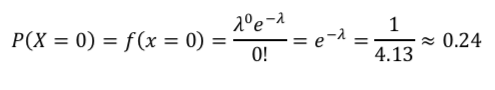
統計検定2級の過去問解説(2017年11月):問12(1)
データの数を知るためには、自由度を読み取る必要があります。
自由度はdegree of freedomもしくは、DFと表記されます。
2通りの読み取り方があります。
1つ目は、Residual standard errorのdegree of freedomに着目する方法。
Residual standard errorとは、残差の標準誤差のことです。
この時の199 degree of freedomは、(データの数-説明変数の数-1)から算出されます。
この問題では、説明変数はlog(販売価格)の1つだけです。
そのため、199=X-1-1が成り立ちます。
よって、X=201となります。
2つ目は、F-statisticのDFに着目する方法です。
「1 and 199 DF」は、「説明変数の数 and 残差 DF」を示しています。
そのため同様に、199=X-1-1の関係式が成り立ちますので、X=201となります。
統計検定2級の過去問解説(2017年11月):問12(2)
回帰係数の検定統計量は、t統計量を用います。
帰無仮説をβ0とし、得られた回帰係数の推定値をβ1、その標準誤差をSE
とすると
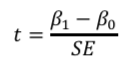
で求めることができる
よって、t統計量は値を代入して以下のようになります。
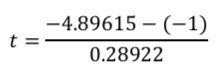
統計検定2級の過去問解説(2017年11月):問12(3)
出力結果を回帰モデルに当てはめると、以下のようになる。
log(販売数量) = 7.92546 – 4.89615 * log(販売価格)
I:◯
正しいです。
回帰係数の解釈としては、説明変数(今回の問題ではlog(販売価格))が1大きくなった場合に、応答変数(今回の問題ではlog(販売数量))がどれだけ変動するか、を示した数値です。
II:◯
正しいです。
logは単調減少、単調増加するため、Iのとおり販売価格が大きくなると販売数量は小さくなります。
III:×
上記の回帰モデルに数値を当てはめます。
すると9.39となるため、誤りです。
統計検定2級の過去問解説(2017年11月):問13(1)
母比率の95%信頼区間の問題です。
統計検定2級では頻出の問題なので、解き方はしっかり理解しておきましょう。
「非常に関心がある」かそうではないかは、二項分布に従うと考えられます。
そのため、推定値はpであり、分散はp(1-p)で求めることができます。
問題文より、pは0.483です。
また、母比率の95%信頼区間は「推定値±1.96*標準誤差」で求めることができます。
この時、標準誤差は「(分散/データ数)のルート」で求めることができます。
以上より、95%信頼区間の式は以下の通りになります。
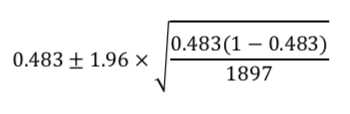
これを求めると、[0.461, 0.505]となる。
統計検定2級の過去問解説(2017年11月):問13(2)
差の95%信頼区間は以下の数式で解くことができる。
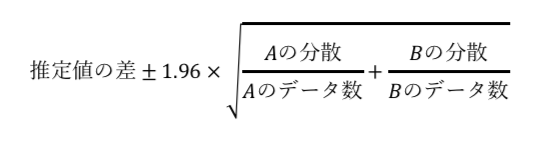
よって、この数式に与えられた問題文の数値を代入する。
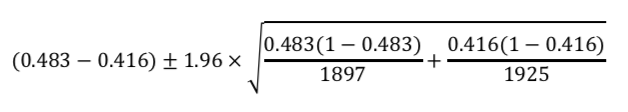
これを解くと、95%信頼区間は[0.036, 0.098]となる。
95%信頼区間が0を含まないため、有意水準5%で母比率の差は0でないと言える。
よって、有意水準5%で変化したと言える。
統計検定2級の過去問解説(2017年11月):問14
I:×
II:◯
その通り。
III:◯
P値は確率であるため、確率の性質上1を超えることはない。
P値、有意水準、有意差の使い分けに関してはこちらの記事を参照してください。
統計検定2級の過去問解説(2017年11月):問15
適合度検定において、 カイ2乗統計量は以下の通り。

いま、問題文で与えられている数値を2つの表にしてみる。
1つは、50人がくじを引いた時、本当に1等が20%、2等が30%であったときに、期待される人数の表。
以下の通りになる。
| 1等 | 2等 | ハズレ | 合計 |
| 10人 (50*0.2) | 15人 (50*0.3) | 25人 | 50人 |
もう1つが、観測されたデータの表。
以下の通りになる。
| 1等 | 2等 | ハズレ | 合計 |
| 5人 | 12人 | 33人 | 50人 |
この2つの表から、カイ二乗値を計算する。
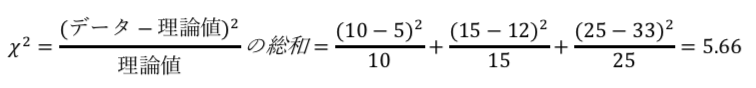
このとき、データの表の自由度は2である。
付表から、自由度2のカイ二乗分布の上側5%の値は5.99である。
よって、得られた値の方が小さいため、帰無仮説は棄却されない。
統計検定2級の過去問解説(2017年11月):問16(1)
全体の平均は以下の式で求めることができる。

よって、与えられた表から数字を代入すると
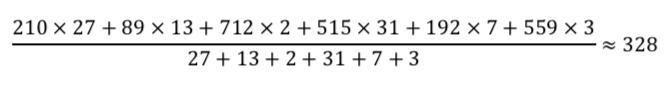
統計検定2級の過去問解説(2017年11月):問16(2)
難問です。
回帰分析でのF値は以下の数式で求めることができます。

今回のデータでは6カ国あるため、水準間の自由度は6-1=5
残差の自由度は、83-5-1=77となります。
これらを踏まえて、F値を数学記号をつかって表現すると
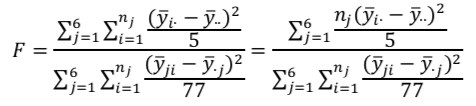
統計検定2級の過去問解説(2017年11月):問16(3)
I:◯
出力結果より、P値は1%より小さい。
よって、F値は上側1%点のF値より大きい。
II:×
99%信頼区間は以下のように求めることができる。
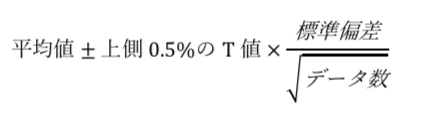
よって、各地域の99%信頼区間を計算すると以下のようになる。
| アジア | アフリカ | オセアニア | ヨーロッパ | 南アメリカ | 北アメリカ |
| 210±92 | 89±57 | 712±90 | 515±66 | 192±143 | 559±1452 |
例えばアジアの99%信頼区間は[118, 302]であり、ヨーロッパの99%信頼区間は[459, 581]であるため、重ならない。
III:×
出力結果から、P値は5%より小さい。











コメント